混合精度训练原理之float16和float32数据之间的互相转换

本篇文章参考：全网最全-混合精度训练原理

• 上述文章已经讲解的比较详细，本文只是从数值角度分析：
  1. float32转入float16的精度误差
  2. 在深度学习的混精度训练当中，当参数值（float32)获取到计算得到的梯度值（float16)后的更新过程。

问题一：float32转入float16的精度误差

首先，我们还是回顾一下float16和float32在计算机当中的存储格式：

有了上述内容之后，我们通过一个实际的例子来观察，float32到float16的舍入误差：(我们使用python的numpy作为例子演示，当用到具体框架如pytorch将其转化为Tensor再进行转化是一样的）

• 当我们创建了一个十进制数据[1.12156456132]，并通过float32进行存储。

big_value32 = np.array([1.12156456132], np.float32)
print(f"big_value32:{big_value32[0]:.23f}")

//result:
big_value32:1.12156450748443603515625

不考虑计算机存储，我们使用十进制转二进制得到【1.12156456132 】的二进制表示为【1.000111110001111011011010111001110011100011010100001…】,它是一个不能在有限精度内存储的数据，根据上述float32的存储空间表示，我们知道它只能保存23位有效数字（不包含首位的1），截取后，他在计算机中的表示为【1.00011111000111101101101】（截取时查看后一位，为1时进一位，为0时不进位），故其十进制表示为【1.12156450748443603515625】（所以在存取数字时是有损失的），舍入为float16时，计算的存储表示为【1.0001111100】，表示为十进制为 【1.12109375】 ，这个时候便产生了舍入误差。

问题二：在深度学习的混精度训练当中，当参数值（float32)获取到计算得到的梯度值（float16)后的更新过程。

• 在混精度训练中，为什么一定要保存一份float32的权重副本用于和计算得出的float16数据做更新？因为如果用float16和float16做计算（加法），相对于float32，会造成精度的损失，甚至导致无法更新。

1. 我们仍然举一个例子来说明这个问题，我们考虑一个十进制的原始数据（权重），假设为【1.125】，利用float16二进制存储为【0 01111 0010000000】，float32二进制存储为【0 01111111 00100000000000000000000】。
2. 同时考虑一个计算得出的float16梯度，假设为【0.12457275190625】，二进制float16表示为【0 01011 1111111001】。
3. 我们使用float16的原始权重去做更新：即【0 01111 0010000000】+【0 01011 1111111001】，由于他们的指数部分不相同，我们需要将指数较小的数据的小数点向左移，以保证他们的指数部分对齐，【0 01011 1111111001】将指数部分对齐【0 01111 0010000000】后，小数点需要向左移4位，在左边补0，移位之后的结果为【0 01111 0001111111】。
4. 将两者的有效位部分相加，即【0010000000】（0）+【0001111111】（1），括号里面表示第11位有效位数值，用于进位，根据二进制加法，我们综合符号位和指数为，得到最后结果为：【0 01111 0100000000】，转换为十进制为【1.250】。

1. 跟上个例子一样，但我们考虑使用float32去和新计算出来的float16数据做计算，在计算过程中，float16会被转换为更高精度的float32参与计算。
2. 二进制float16【0 01011 1111111001】转换为float32为【0 01111011 11111110010000000000000】（指数位+122，有效位数后面补0）。
3. 进行加法计算【0 01111111 00100000000000000000000】+【0 01111011 11111110010000000000000】，算得最后结果为【0 01111111 00111111111001000000000】，转换为十进制为【1.24957275390625】。从中我们可以看到精度的损失，这也是为什么要保存权重的高精度副本用于更新。

• 如果还有理解不到位的地方，可以配合这两个工具食用：
  • 在线IEEE浮点二进制计算器
  • 在线进制转换

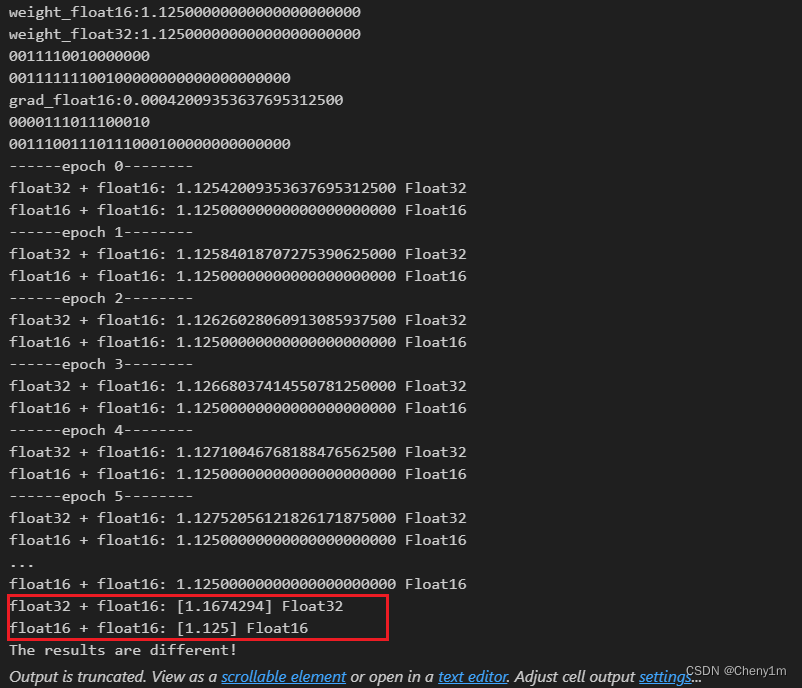
附：1.更新失效例子（mindspore代码）：

import numpy as np
import mindspore as ms
from mindspore import Tensor
import struct

def float_to_bin(num):
    return format(struct.unpack('!I', struct.pack('!f', num))[0], '032b')

def float16_to_bin(num):
    float16 = np.float16(num)
    int_bits = np.frombuffer(float16.tobytes(), dtype=np.uint16)[0]
    bin_str = format(int_bits, '016b')
    return bin_str


big_value32 = np.array([1.125], np.float32)
big_value16 = big_value32.astype(np.float16)  # 转换为float16

print(f"weight_float16:{big_value16[0]:.23f}")
print(f"weight_float32:{big_value32[0]:.23f}")
print(float16_to_bin(big_value16[0]))
print(float_to_bin(big_value32[0]))


small_value_float16 = np.array([0.00041999], np.float16) 

print(f"grad_float16:{small_value_float16[0]:.23f}")
print(float16_to_bin(small_value_float16[0]))
print(float_to_bin(small_value_float16[0]))


# 在MindSpore中进行计算
small_tensor_float16 = Tensor(small_value_float16, ms.float16)
big_tensor16 = Tensor(big_value16, ms.float16)
big_tensor32 = Tensor(big_value32, ms.float32)

# float32与float16相加
print(f"------epoch 0--------")
result1 = big_tensor32 + small_tensor_float16
print(f"float32 + float16: {result1.asnumpy()[0]:.23f}",result1.dtype)
result2 = big_tensor16 + small_tensor_float16
print(f"float16 + float16: {result2.asnumpy()[0]:.23f}",result2.dtype)
for i in range(100):
    print(f"------epoch {i+1}--------")
    result1 += small_tensor_float16
    print(f"float32 + float16: {result1.asnumpy()[0]:.23f}",result1.dtype)
    result2 += small_tensor_float16
    print(f"float16 + float16: {result2.asnumpy()[0]:.23f}",result2.dtype)

    
print("float32 + float16:", result1.asnumpy(),result1.dtype)
print("float16 + float16:", result2.asnumpy(),result2.dtype)

if not np.isclose(result1.asnumpy(), result2.asnumpy()):
    print("The results are different!")
else:
    print("The results are the same!")

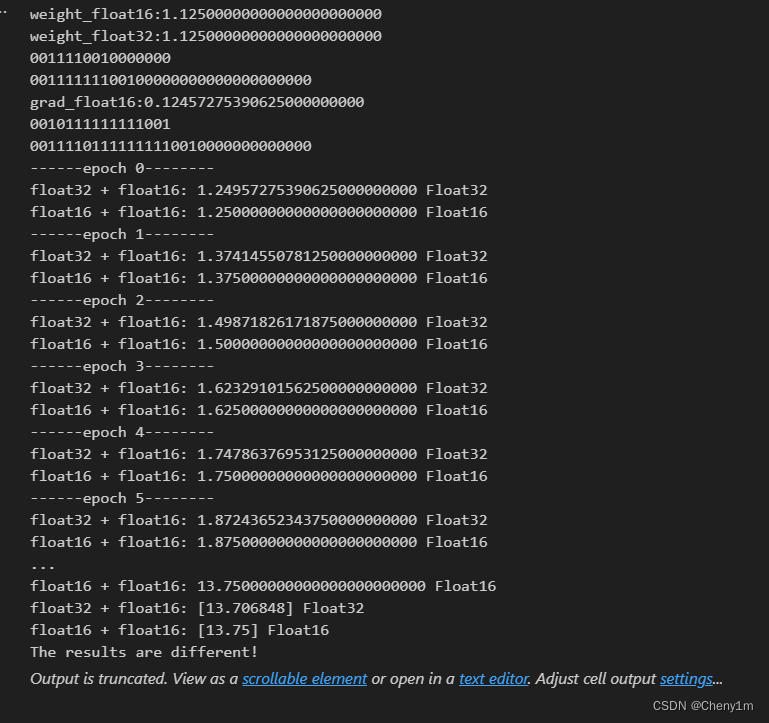
2.误差累积例子：将上述small_value_float16改为0.12457275190625，即可得到问题2，例子2中观察：