题目：718. 最长重复子数组

Leetcode题目地址
题目描述：
给两个整数数组 nums1 和 nums2 ，返回两个数组中公共的、长度最长的子数组的长度。

示例 1：

输入：nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]
输出：3
解释：长度最长的公共子数组是 [3,2,1] 。

示例 2：

输入：nums1 = [0,0,0,0,0], nums2 = [0,0,0,0,0]
输出：5

提示：

1 <= nums1.length, nums2.length <= 1000
0 <= nums1[i], nums2[i] <= 100

本题重难点

注意题目中说的子数组，其实就是连续子序列。

要求两个数组中最长重复子数组，如果是暴力的解法只要需要先两层for循环确定两个数组起始位置，然后在来一个循环可以是for或者while，来从两个起始位置开始比较，取得重复子数组的长度。

本题其实是动规解决的经典题目，我们只要想到 用二维数组可以记录两个字符串的所有比较情况，这样就比较好推递推公式了。
动规五部曲分析如下：

确定dp数组（dp table）以及下标的含义
dp[i][j] ：以下标i - 1为结尾的nums1，和以下标j - 1为结尾的nums2，最长重复子数组长度为dp[i][j]。 （特别注意： “以下标i - 1为结尾的nums1” 标明一定是以nums1[i-1]为结尾的字符串）
此时细心的同学应该发现，那dp[0][0]是什么含义呢？总不能是以下标-1为结尾的nums1数组吧。
其实dp[i][j]的定义也就决定着，我们在遍历dp[i][j]的时候i 和 j都要从1开始。
那有同学问了，我就定义dp[i][j]为以下标i为结尾的nums1，和以下标j 为结尾的nums2，最长重复子数组长度。不行么？
行倒是行！但实现起来就麻烦一点，需要单独处理初始化部分，在本题解下面的拓展内容里，我给出了第二种 dp数组的定义方式所对应的代码和讲解，大家比较一下就了解了。
确定递推公式
根据dp[i][j]的定义，dp[i][j]的状态只能由dp[i - 1][j - 1]推导出来。
即当nums1[i - 1] 和nums2[j - 1]相等的时候，dp[i][j] = dp[i - 1][j - 1] + 1;
根据递推公式可以看出，遍历i 和 j 要从1开始！
dp数组如何初始化
根据dp[i][j]的定义，dp[i][0] 和dp[0][j]其实都是没有意义的！
但dp[i][0] 和dp[0][j]要初始值，因为为了方便递归公式dp[i][j] = dp[i - 1][j - 1] + 1;
所以dp[i][0] 和dp[0][j]初始化为0。
举个例子nums1[0]如果和nums2[0]相同的话，dp[1][1] = dp[0][0] + 1，只有dp[0][0]初始为0，正好符合递推公式逐步累加起来。
确定遍历顺序
外层for循环遍历nums1，内层for循环遍历nums2。
那又有同学问了，外层for循环遍历nums2，内层for循环遍历nums1。不行么？
也行，一样的，我这里就用外层for循环遍历nums1，内层for循环遍历nums2了。
同时题目要求长度最长的子数组的长度。所以在遍历的时候顺便把dp[i][j]的最大值记录下来。
代码如下：

for (int i = 1; i <= nums1.size(); i++) {
    for (int j = 1; j <= nums2.size(); j++) {
        if (nums1[i - 1] == nums2[j - 1]) {
            dp[i][j] = dp[i - 1][j - 1] + 1;
        }
        if (dp[i][j] > res) res = dp[i][j];
    }
}

举例推导dp数组

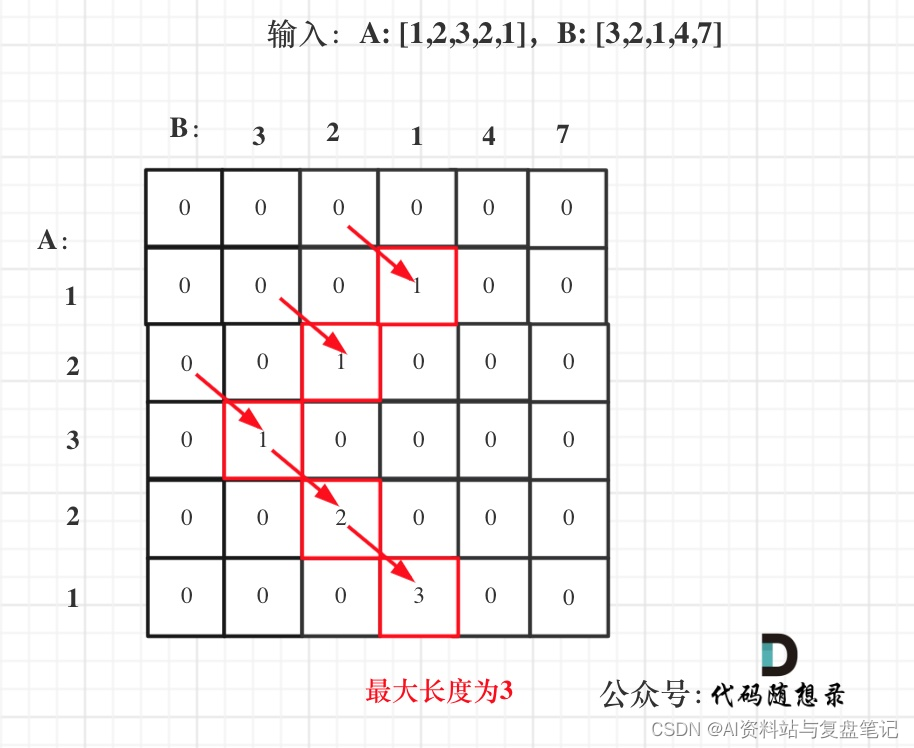
拿示例1中，A: [1,2,3,2,1]，B: [3,2,1,4,7]为例，画一个dp数组的状态变化，如下：

方法一、动态规划未优化代码

C++代码

class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        vector<vector<int>>dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));
        int res = 0;
        for(int i = 1; i <= nums1.size(); i++){
            for(int j = 1; j <= nums2.size(); j++){
                if(nums1[i - 1] == nums2[j - 1]){
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }
                if(dp[i][j] > res){
                    res = dp[i][j];
                }
            }
        }
        return res;
    }
};

时间复杂度： $O (n \times m)$ ，n 为nums1长度，m为nums2长度
空间复杂度： $O (n \times m)$

方法二、动态规划优化代码

我们可以看出dp[i][j]都是由dp[i - 1][j - 1]推出。那么压缩为一维数组，也就是dp[j]都是由dp[j - 1]推出。

也就是相当于可以把上一层dp[i - 1][j]拷贝到下一层dp[i][j]来继续用。

此时遍历nums2数组的时候，就要从后向前遍历，这样避免重复覆盖。

C++代码

class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        vector<int>dp(nums2.size() + 1, 0);
        int res = 0;
        for(int i = 1; i <= nums1.size(); i++){
            for(int j = nums2.size(); j > 0 ; j--){
                if(nums1[i - 1] == nums2[j - 1]){
                    dp[j] = dp[j - 1] + 1;
                }
                else{
                    dp[j] = 0; // 注意这里不相等的时候要有赋0的操作
                }
                if(dp[j] > res){
                    res = dp[j];
                }
            }
        }
        return res;
    }
};

时间复杂度： $O (n \times m)$ ，n 为nums1长度，m为nums2长度
空间复杂度： $O (m)$

拓展

前面讲了 dp数组为什么定义：以下标i - 1为结尾的nums1，和以下标j - 1为结尾的nums2，最长重复子数组长度为dp[i][j]。

我就定义dp[i][j]为以下标i为结尾的nums1，和以下标j 为结尾的nums2，最长重复子数组长度。不行么？

当然可以，就是实现起来麻烦一些。

如果定义 dp[i][j]为以下标i为结尾的nums1，和以下标j 为结尾的nums2,那么第一行和第一列毕竟要经行初始化，如果nums1[i] 与 nums2[0] 相同的话，对应的 dp[i][0]就要初始为1，因为此时最长重复子数组为1。 nums2[j] 与 nums1[0]相同的话，同理。

所以代码如下：

class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        vector<vector<int>> dp (nums1.size() + 1, vector<int>(nums2.size() + 1, 0));
        int res = 0;

        // 要对第一行，第一列经行初始化
        for (int i = 0; i < nums1.size(); i++) if (nums1[i] == nums2[0]) dp[i][0] = 1;
        for (int j = 0; j < nums2.size(); j++) if (nums1[0] == nums2[j]) dp[0][j] = 1;

        for (int i = 0; i < nums1.size(); i++) {
            for (int j = 0; j < nums2.size(); j++) {
                if (nums1[i] == nums2[j] && i > 0 && j > 0) { // 防止 i-1 出现负数
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }
                if (dp[i][j] > res) res = dp[i][j];
            }
        }
        return res;
    }
};