数据结构与算法java篇--二叉树

news2024/11/18 3:38:18

内容有点多，建议先收藏

目录

一.树的介绍

二.java代码实现树

1.Node类

2.Tree类

3.查找节点

4.插入节点  

5.遍历树

        5.1 中序遍历

        5.2 前序遍历和后序遍历

6.查找最大值和最小值

7.删除节点

        7.1 删除没有子节点的节点

        7.2 删除有一个子节点的结点

        7.3 删除有两个节点的节点 

8. 完整的二叉树java代码

一.树的介绍

树由边连接的节点而组成，在图中用圆表示节点，实现表示边

 路径：顺着节点从一个节点到另一个节点的顺序叫做路径

根：树顶端的节点叫根

父节点：连接下层节点的上层节点称为父节点，例如B是C,D的父节点

子节点：和父节点相连接的节点

叶节点：没有子节点的节点

二.java代码实现树

1.Node类

Node类是节点对象的类，包含了对象的数据

Node类的实现：

class Node{
    int iData;    //节点的键
    double fData;   //数据
    Node leftChild;   //左节点
    Node rightChild;  //右节点
}

Node类对象还可以指向一个代表数据类型的对象，而不是把数据项直接放在节点中：

class Node{
   person p1;
    Node leftChild;
    Node rightChild;
}
class person{
    int iData;
    double fData;
}

2.Tree类

Tree类是一个数本身的类，Tree类中有查询，删除，插入以及遍历和显示的方法

 Tree类的骨架：

class Tree{
    private Node root;  //根节点
    public void insert(int id,double dd){
        
    }
    public void find(int key){
        
    }
    public void delete(int id){
        
    }
    //.......
}

3.查找节点

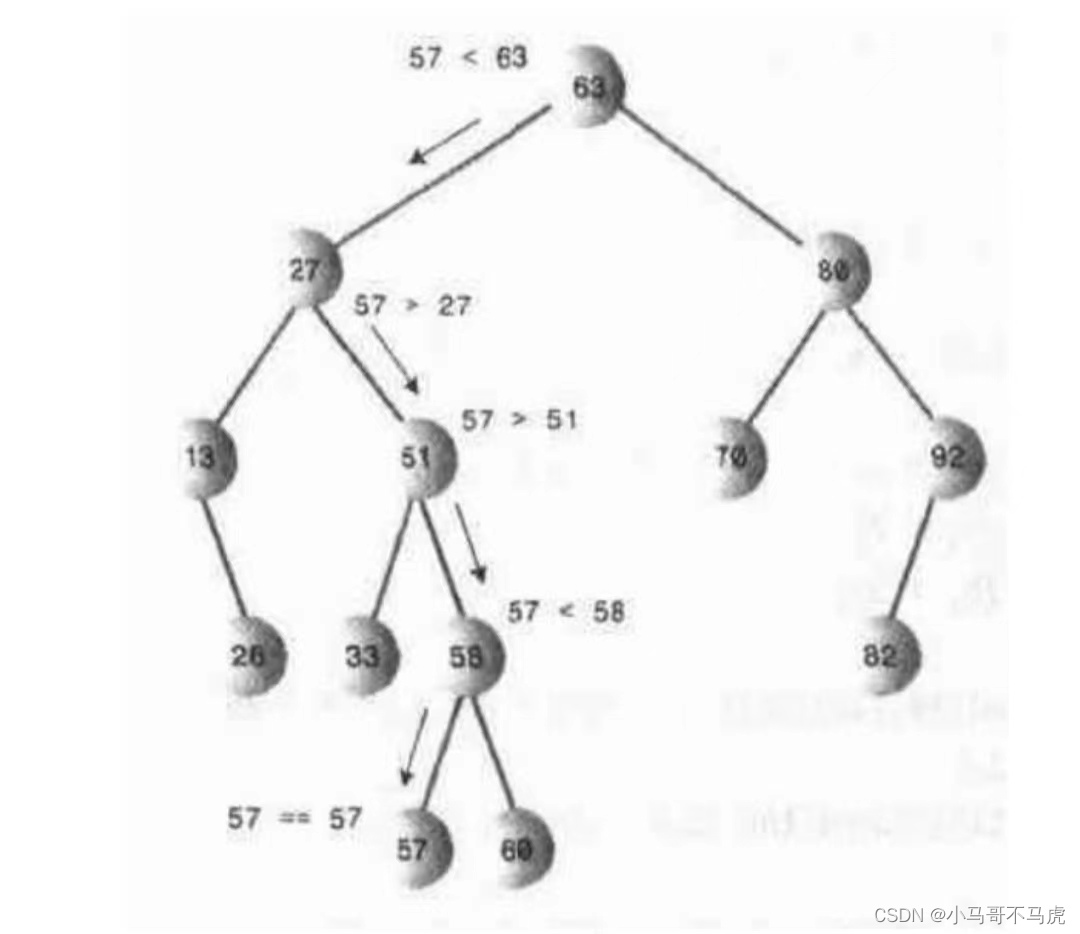
规定父节点的左节点小于父节点，右节点小于父节点，在查找是，最先和父节点比较，如果查找的对象小父节点就在父节点的左节点查找，反之在右节点查找，如此类推，直到找到

查找代码：

 public Node find(int key){
        Node current=root;
        while(current.iData!=key){
            if(key<current.iData)    //如果小于
                current=current.leftChild;
            else       //如果大于
                current=current.rightChild;
            if (current==null)
                return null;
        }
        return current;
    }

4.插入节点  

插入节点，先查找到插入节点的父节点，如果插入的值大于父节点就插入到右节点，反之插入左节点

 插入操作代码：

 public void insert(int id,double dd){
        Node newNode=new Node();
        newNode.iData=id;
        newNode.dData=dd;
        if (root==null)
            root=newNode;
        else {
            Node current=root;
            Node parent;
            while (true){
                parent=current;
                if(id<current.iData){
                    current=current.leftChild;
                    if (current==null){
                        parent.leftChild=newNode;
                        return;
                    }
                    else {
                        current=current.rightChild;
                        if (current==null){
                            parent.leftChild=newNode;
                            return;
                        }
                    }
                }
            }
        }
    }

5.遍历树

遍历树就是按顺序访问树的每一个节点，遍历有分为中序遍历，前序遍历和后序遍历

5.1 中序遍历

图解中序遍历：

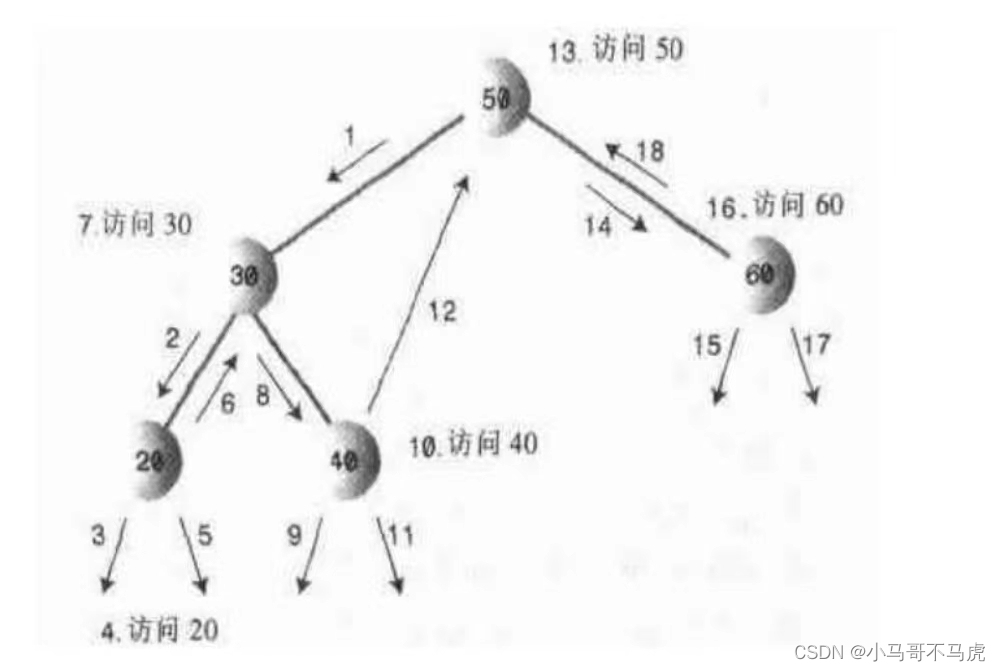
 从节点开始沿左边画路径线，当路径线结果节点正下方时该结点被遍历,如图遍历结果：20,30,40,50,60

中序遍历代码：

 public void inOrder(Node localRoot){
        if (localRoot!=null){
            inOrder(localRoot.leftChild);
            System.out.print(localRoot.iData+" ");
            inOrder(localRoot.rightChild);
        }
    }

5.2 前序遍历和后序遍历

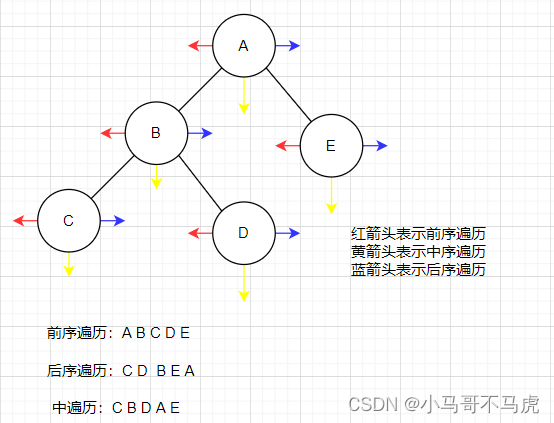
前序遍历和后序遍历的方法类似于中序遍历

6.查找最大值和最小值

二叉树查找最小值只要遍历左子树，遍历的最后一个就是最小的，反之，遍历右子树，最后一个就是最大的

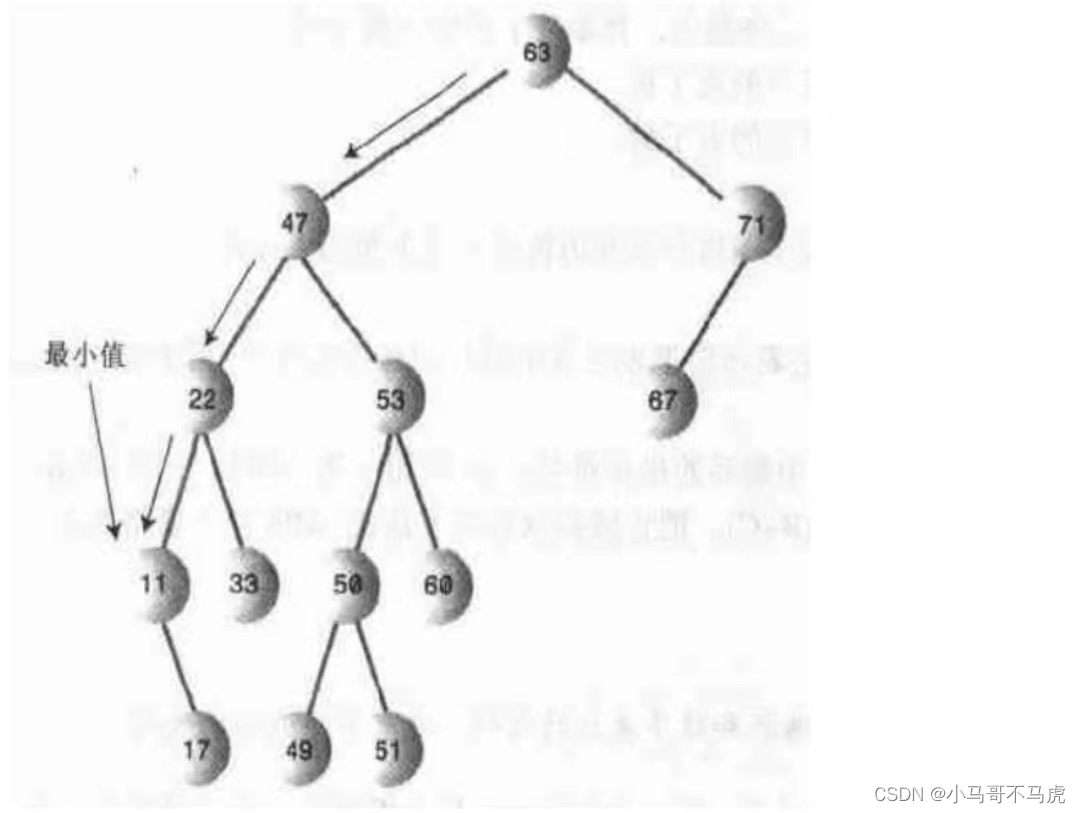
 如·图是查找最小值，查找最小值代码：

public Node minmum(){
        Node current,last;
        current=root;
        while (current!=null){
            last=current;
            current=current.leftChild;
        }
        return last;
}

查找最大值：

public Node minmum(){
        Node current,last;
        current=root;
        while (current!=null){
            last=current;
            current=current.rightChild;
        }
        return last;
}

7.删除节点

删除节点只要让该节点为null就可以了，虽然该节点依然存在，但java的垃圾回收处理会清除该节点，实现删除节点，删除操作要考虑三种情况：

1.该节点是叶节点

2.该节点有一个子节点

3.该节点有两个子节点

7.1 删除没有子节点的节点

删除没有叶节点，只要改变其父节点对应的子节点的值即可

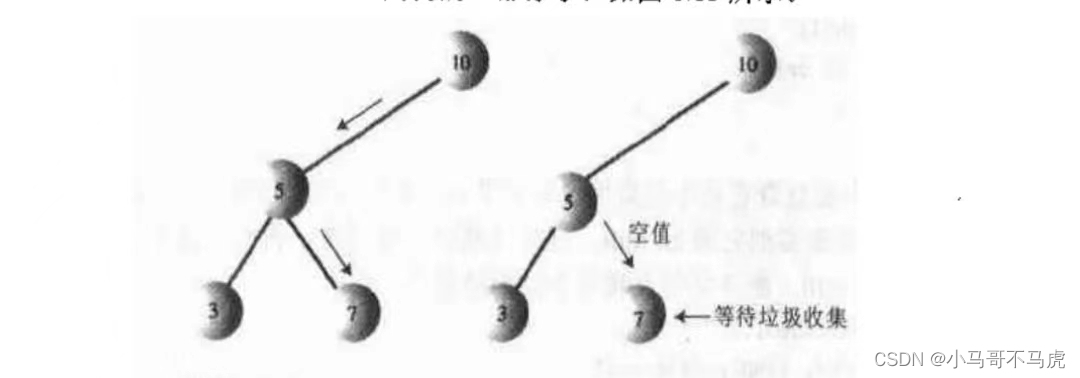
代码：

public boolean delete(int key){
        Node current=root;
        Node parent=root;
        boolean isLeftChild=true;
        while (current.iData!=key){
            parent=current;
            if(key<current.iData){
                isLeftChild=true;
                current=current.leftChild;
            }
            else {
                isLeftChild=false;
                current=current.rightChild;
            }
            if(current==null)
                return false;
        }
        if (current.leftChild==null&&current.rightChild==null){   //如果是叶节点
            if (current==root)
                root=null;
            else if(isLeftChild)
                parent.leftChild=null;
            else parent.rightChild=null;
        }
        return true;
}

7.2 删除有一个子节点的结点

  删除有一个子节点时，只要将该节点的子节点和其父节点连接即可

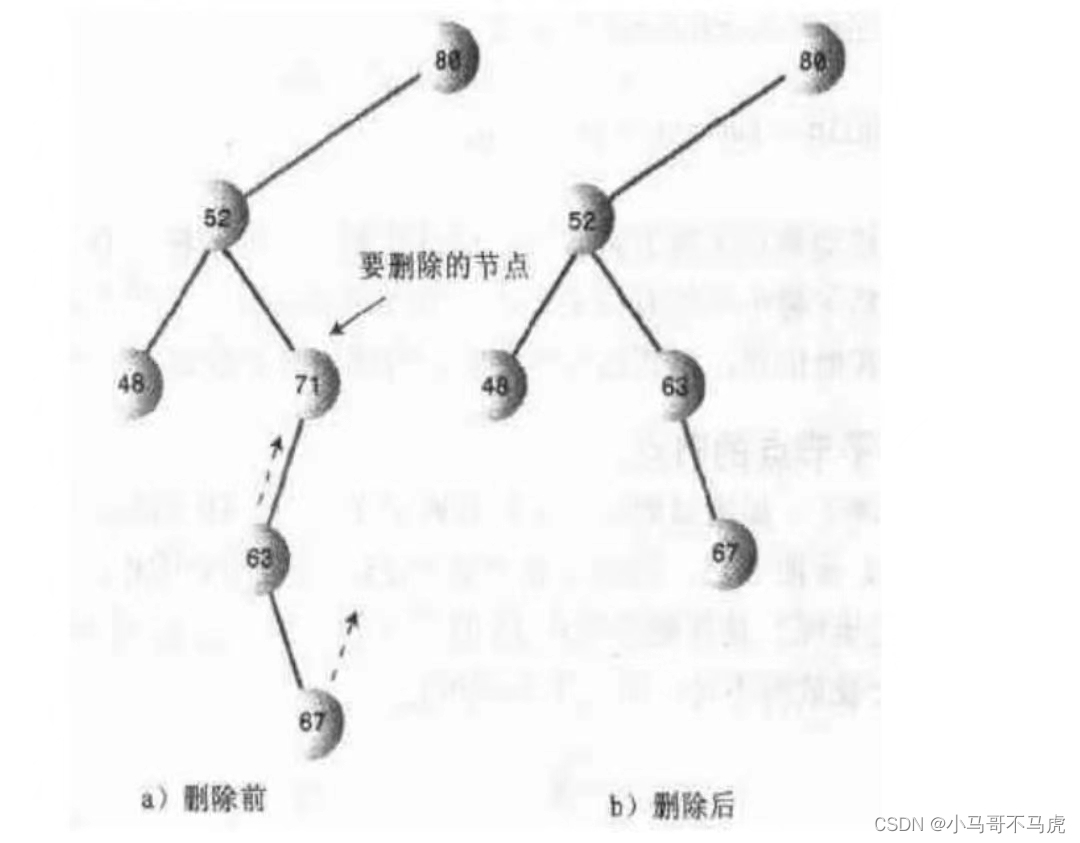
 部分代码：

      else if(current.rightChild==null)
            if (current==root)
                root=current.leftChild;
        else if(isLeftChild)
            parent.leftChild=current.rightChild;
        else if(current.leftChild==null)
            if(current==root)
                root=current.rightChild;
            else if(isLeftChild)
                parent.leftChild=current.rightChild;
            else 
                parent.rightChild=current.rightChild;

7.3 删除有两个节点的节点 

 删除有两个节点的节点，要找到一个结点和父节点连接，同时该连接的结点要满足大于删除节点的左节点，小于删除节点的右节点，我们称该点为后继点

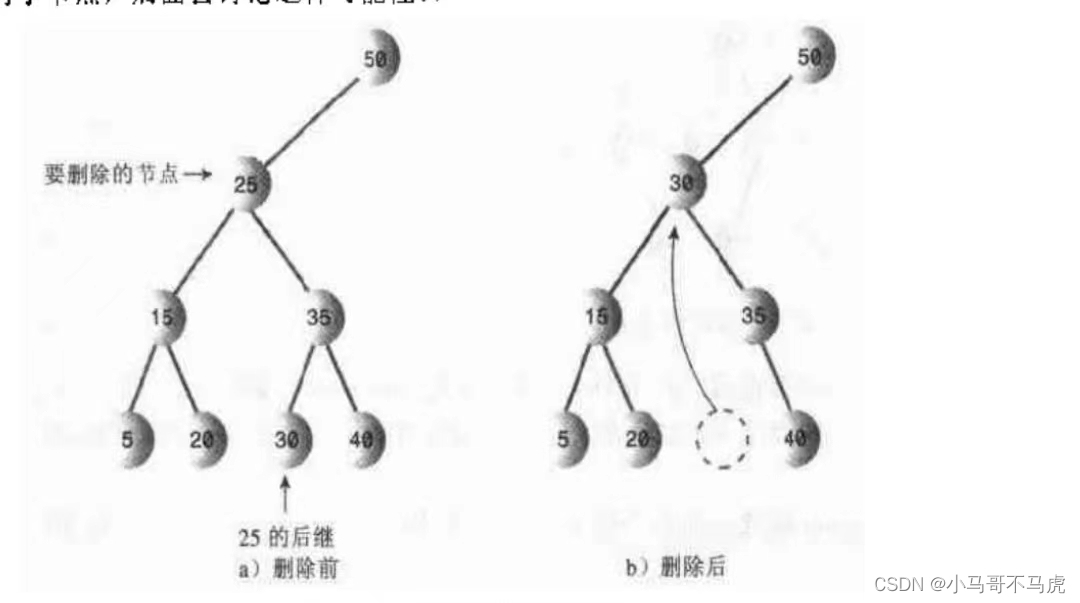 查找后继点的代码：

public Node getSuccessor(Node delNode){
        Node successorParent=delNode;
        Node successor=delNode;
        Node current=delNode.rightChild;
        while (current!=null){
            successorParent=successor;
            successor=current;
            current=current.leftChild;
        }
        if(successor!=delNode.rightChild){
            successorParent.leftChild=successor.rightChild;
            successor.rightChild=delNode.rightChild;
        }
        return successor;
}

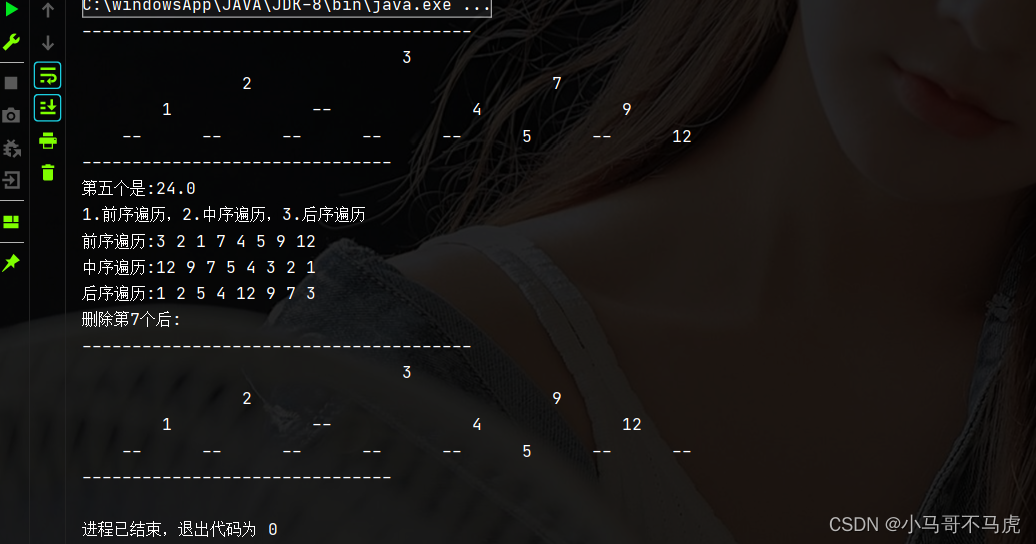
8. 完整的二叉树java代码

public class Mains {
    public static void main(String[] args){
        Tree tree=new Tree();
        tree.insert(3,23);
        tree.insert(2,56);
        tree.insert(1,43);
        tree.insert(7,58);
        tree.insert(9,49);
        tree.insert(12,62);
        tree.insert(4,93);
        tree.insert(5,24);
        tree.displayTree();
         Node node=tree.find(5);
         System.out.println("第五个是:"+node.dData);
         System.out.println("1.前序遍历，2.中序遍历，3.后序遍历");
         tree.traverse(1);
        tree.traverse(2);
        tree.traverse(3);
         tree.delete(7);
         System.out.println("删除第7个后:");
         tree.displayTree();
    }
}

class Node{   //节点
    public int iData;
    public double dData;
    public Node leftChild;
    public Node rightChild;
    public void display(){
        System.out.print("{");
        System.out.print(iData);
        System.out.print(",");
        System.out.print("}");
    }
}

class Tree{    //树结构
    private Node root;
    public Tree(){
        root=null;
    }
    public Node find(int key){   //查找操作
        Node current=root;
        while (current.iData!=key){
            if(key<current.iData)   //如果小于，在左子树查找
                current=current.leftChild;
            else                    //如果大于，在右子树查找
                current=current.rightChild;
            if(current==null)  //如果没有找到
                return null;
        }
        return current;   //如果找到，返回current
    }
            //插入操作
    public void insert(int id,double dd){
        Node newNode=new Node();
        newNode.iData=id;
        newNode.dData=dd;
        if(root==null)  //如果根节点为空
            root=newNode;
        else {
            Node current=root; //遍历开始位置
            Node parent;
            while (true){
                parent=current;
                if(id<current.iData){  //小于当前二叉树键，在左子树插入
                    current=current.leftChild;
                    if (current==null){  //插入左子树最后一个
                        parent.leftChild=newNode;
                        return;
                    }
                }else {   //目标键大于时，在右子树插入
                    current=current.rightChild;
                    if (current==null){   //插入到右子树最后一个
                        parent.rightChild=newNode;
                        return;
                    }
                }
            }
        }
    }
    //删除操作
    public boolean delete(int key){
        Node current=root;
        Node parent=root;
        boolean isleftChild=true;
        while (current.iData!=key) {
            parent = current;    //设置父节点
            if (key < current.iData) { //左边操作
                isleftChild = true;   //表示删除的节点在左节点上
                current = current.leftChild;
            } else {    //右边查找
                isleftChild = false;
                current = current.rightChild;
            }
            if (current == null)  //如果没有找到要删除的key
                return false;
        }
            //叶节点的删除操作
            if(current.leftChild==null&&current.rightChild==null){
                if (current==root)  //如果该叶节点为根
                    root=null;
                else if (isleftChild) //如果删除的是左节点
                    parent.leftChild=null;    //删除操作
                else
                    parent.rightChild=null;   //删除操作
            }
            //有一个节点的删除操作
            else if (current.rightChild==null) //只有一个左节点
                if (current==root)
                    root=current.leftChild;
                else if (isleftChild)  //如果删除的是左节点
                    parent.leftChild=current.leftChild; //该删除节点的左节点连接该父节点
                else
                    parent.rightChild=current.leftChild;  该删除节点的右节点连接该父节点
            else if (current.leftChild==null) //只有一个右节点
                if (current==root)
                    root=current.rightChild;
                else if (isleftChild)
                    parent.leftChild=current.rightChild;
                else
                    parent.rightChild=current.rightChild;
            else {    //有两个节点的删除，先找后继点
                Node successor = getSuccessor(current);  //调用getSuccessor寻找后继点
                if (current == root)
                    root = successor;
                else if (isleftChild)  //后继点是左节点
                    parent.leftChild = successor;
                else
                    parent.rightChild = successor;
                successor.leftChild = current.leftChild;   //没有后继点
            }
        return true;
    }
    //后继节点查找操作
    private Node getSuccessor(Node delNode){
        Node successorParent=delNode;
        Node successor=delNode;
        Node current=delNode.rightChild;  //从被删除节点的右节点查找
        while (current!=null){
            successorParent=successor;
            successor=current;
            current=current.leftChild;  //后继节点在左节点
        }
        if (successor!=delNode.rightChild){  //如果后继节点不是第一节点
            successorParent.leftChild=successor.rightChild;   //后继点的右节点连接后继节点父节点的左节点
            successor.rightChild=delNode.rightChild;     //被删除节点的右节点连接后继节点的右节点
        }
        return successor;
    }
  //选择遍历方式操作
  public void traverse(int travesType){
        switch (travesType){
            case 1:System.out.print("前序遍历:");
                    preOrder(root);
                    break;
            case 2:System.out.print("中序遍历:");
                    inOrder(root);
                    break;
            case 3:System.out.print("后序遍历:");
                    postOrder(root);
                    break;
        }
        System.out.println(" ");
    }
    //前序遍历
    private void preOrder(Node locaRoot){
        if(locaRoot!=null){
            System.out.print(locaRoot.iData+" ");
            preOrder(locaRoot.leftChild);
            preOrder(locaRoot.rightChild);
        }
    }
    //中序遍历
    private void inOrder(Node locaRoot){
        if (locaRoot!=null){
            inOrder(locaRoot.rightChild);
            System.out.print(locaRoot.iData+" ");
            inOrder(locaRoot.leftChild);
        }
    }
    //后序遍历
    private void postOrder(Node locaRoot){
        if (locaRoot!=null){
          postOrder(locaRoot.leftChild);
          postOrder(locaRoot.rightChild);
          System.out.print(locaRoot.iData+" ");
        }
    }
    //显示操作
    public void displayTree(){
        Stack globalStack=new Stack();
        globalStack.push(root);
        int nBlank=32;
        boolean isRowEmpty=false;
        System.out.println("---------------------------------------");
        while (isRowEmpty==false){
            Stack localStack=new Stack();
            isRowEmpty=true;
            for (int j=0;j<nBlank;j++)
                System.out.print(" ");
            while (globalStack.isEmpty()==false){
                Node temp=(Node)globalStack.pop();
                if(temp!=null){
                    System.out.print(temp.iData);
                    localStack.push(temp.leftChild);
                    localStack.push(temp.rightChild);
                    if (temp.leftChild!=null || temp.rightChild!=null)
                        isRowEmpty=false;
                }else {
                    System.out.print("--");
                    localStack.push(null);
                    localStack.push(null);
                }
                for (int i=0;i<nBlank*2-2;i++)
                    System.out.print(" ");
            }
            System.out.println( );
            nBlank/=2;
            while (localStack.isEmpty()==false)
                globalStack.push(localStack.pop());
        }
        System.out.println("-------------------------------");
    }
}

运行：

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/113104.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

java美食论坛系统发帖子系统美食论坛网站美食分享论坛源码

java美食论坛系统发帖子系统美食论坛网站美食分享论坛源码

ssm开发的美食论坛系统&#xff0c;用户注册之后可以发布关于美食的帖子&#xff0c;其他人可以回帖&#xff0c;评论&#xff0c;点赞回复和评论&#xff0c;分为楼主&#xff0c;第一楼&#xff0c;第二楼等。可以再个人中心查看我对别人的回复&#xff0c;以及别人对我的回复…
阅读更多...
学习黑客十余年，如何成为一名安全工程师？

学习黑客十余年，如何成为一名安全工程师？

1. 前言 说实话&#xff0c;一直到现在&#xff0c;我都认为绝大多数看我这篇文章的读者最后终究会放弃&#xff0c;原因很简单&#xff0c;自学终究是一种适合于极少数人的学习方法&#xff0c;而且非常非常慢&#xff0c;在这个过程中的变数过大&#xff0c;稍有不慎&#x…
阅读更多...
主成分分析（PCA）

主成分分析（PCA）

主成分分析是一种降维&#xff08;去除噪声和不重要信息&#xff09;方法&#xff0c;它能将多个指标转换为少数几个主成分&#xff0c;这些主成分是原始变量的线性组合&#xff0c;且彼此之间互不相关。 适用性&#xff1a;当研究的问题涉及到多变量且变量之间存在很强的相关…
阅读更多...
【LeetCode】2099. 找到和最大的长度为 K 的子序列

【LeetCode】2099. 找到和最大的长度为 K 的子序列

【LeetCode】2099. 找到和最大的长度为 K 的子序列 给你一个整数数组 nums 和一个整数 k 。你需要找到 nums 中长度为 k 的 子序列 &#xff0c;且这个子序列的 和最大 。 请你返回 任意 一个长度为 k 的整数子序列。 子序列 定义为从一个数组里删除一些元素后&#xff0c;不…
阅读更多...
BIT.1_常见指令以及权限理解

BIT.1_常见指令以及权限理解

目录使用 XShell 远程登录 Linux下载安装 XShell查看 Linux 主机 ip使用 XShell 登陆主机XShell 下的复制粘贴文件 内容数据 属性数据Linux目录结构相对/绝对路径Linux下基本指令01. ls 指令02. pwd命令03. cd 指令04. touch指令05.mkdir指令&#xff08;重要&#xff09;&am…
阅读更多...
基于Xlinx的时序分析与约束（4）----主时钟约束

基于Xlinx的时序分析与约束（4）----主时钟约束

主时钟约束语法 主时钟约束&#xff0c;就是我们对主时钟&#xff08;Primary Clock&#xff09;的时钟周期进行约束&#xff08;告诉综合工具布局布线的标准&#xff09;&#xff0c;这个约束是我们用的最多的约束了&#xff0c;也是最重要的约束。 主时钟必须与一个网表对象相…
阅读更多...
seo综合查询，怎么看网站在移动端权重高低

seo综合查询，怎么看网站在移动端权重高低

移动权重就是指在手机、IPAD等的流量&#xff0c;数值越大流量越多。 未来百度流量一定会更倾向于移动端&#xff0c;移动端搜索将是百度搜索引擎的主要阵地。这一点和用户上网习惯有关系&#xff0c;因为移动网络无处不在。 那么怎么看网站在移动端权重高低&#xff1f;最…
阅读更多...
Office选装 + Visio安装

Office选装 + Visio安装

一.Office选装 这里我以装Word、Excel和Powerpoint为例 第一步&#xff1a;下载office tool plus 下载地址&#xff1a;https://otp.landian.vip/zh-cn/ 打开网址后&#xff0c;点击红色的立即下载&#xff0c;进入文件存放页面&#xff1b; 第二步&#xff1a;选择其中一个下…
阅读更多...
STM32F103C8T6平衡车

STM32F103C8T6平衡车

链接&#xff1a;https://pan.baidu.com/s/1WJ9otyE9LuO6Kh5gyQ0Tug?pwd8888 提取码&#xff1a;8888 #define BIN2_Pin GPIO_PIN_12 #define BIN2_GPIO_Port GPIOB #define BIN1_Pin GPIO_PIN_13 #define BIN1_GPIO_Port GPIOB #define AIN1_Pin GPIO_PIN_14 #define AIN1_…
阅读更多...
CSS知识点1

CSS知识点1

CSS:层叠样式表 1.行内样式&#xff1a;<h1 style"background-color: aqua;">Hellocss</h1> 仅对当前标签有效 2.内部样式&#xff1a;写在title处 对当前页面有效 3.外部标签&#xff1a;<link rel"stylesheet" href"./js/main…
阅读更多...
干货分享丨超详细的200G QSFP56光模块知识

干货分享丨超详细的200G QSFP56光模块知识

随着数据中心的快速发展&#xff0c;在100G光模块不足以满足日益增长的网络升级要求而400G还未普及的情况下&#xff0c;200G QSFP56光模块成为了200G以太网部署的主流解决方案。接下来&#xff0c;就由易天光通信为你详细介绍一下200G QSFP56光模块。 200G QSFP56光模块是40G…
阅读更多...
供应Biotin-PEG-acid，Biotin-PEG-COOH，生物素-聚乙二醇-羧基

供应Biotin-PEG-acid，Biotin-PEG-COOH，生物素-聚乙二醇-羧基

含有生物素和羧酸的线性杂双功能PEG试剂化学试剂Biotin-PEG-acid /Biotin-PEG-COOH其英文名为&#xff0c;它所属分类为Biotin PEG Carboxylic acid PEG。 peg试剂的分子量均可定制&#xff0c;有&#xff1a;生物素-PEG1-羧基、Biotin-PEG2-COOH、生物素-peg3.4-羧基、Biotin…
阅读更多...
python代码~创意圣诞树

python代码~创意圣诞树

2022年圣诞节到来啦&#xff0c;很高兴这次我们又能一起度过~ 圣诞节(Christmas)本身是一个宗教节&#xff0c;用来庆祝耶稣的诞辰&#xff0c;因而又名耶诞节 Hope all your Christmas dreams come true! 　　 愿你所有的圣诞梦想都成真! 　　 Hope you enjoy the happiness o…
阅读更多...
Express 基本使用（简）

Express 基本使用（简）

前一篇内容讲到Express框架的安装以及对Express项目的目录文件有一定的认识了解之后&#xff0c;使用Express创建了最基本的一个Web服务器&#xff0c;接下来进行对Express框架的一些内容来做一个基本的使用&#xff1b; 创建 Web 服务器 node 或 nodemon 执行app.js文件&#…
阅读更多...
贪心法算法

贪心法算法

目录 一 算法简介 1&#xff09;算法案例引入 2&#xff09;算法思想 3&#xff09;算法概念 4&#xff09; 算法求解的问题的特征 5&#xff09;算法应用 二 算法常见问题 1&#xff09;活动安排问题&#xff08;区间调度问题&#xff09; 今年暑假不AC 2&#xff…
阅读更多...
【QT】信号与槽

【QT】信号与槽

信号与槽 信号(Signal) 与 槽(Slot) 是Qt中对象之间的通信方式&#xff0c;可以用一个简单的栗子说明&#xff1a;当我们想要开灯时&#xff0c;按下开关发出指令&#xff0c;这就是信号&#xff1b;而灯泡接收到电流变化&#xff0c;发出光亮&#xff0c;这就是响应(槽)。 我…
阅读更多...
通过cmd指令创建vue项目

通过cmd指令创建vue项目

通过cmd指令创建vue项目 基础材料&#xff1a; 已安装node.js 已安装 npm&#xff08;安装node.js后会自带安装npm&#xff09; 首先通过node –v和npm –v确保他们都安装了&#xff0c;能够看见版本号就表示ok 然后通过指令安装vue脚手架 npm install -g vue/cli5.0.8 安…
阅读更多...
QTableView表格控件区域选择-自绘选择区域

QTableView表格控件区域选择-自绘选择区域

一、概述 最近优化了一个小功能&#xff0c;主要是模仿excel相关的操作&#xff0c;觉得还挺不错的&#xff0c;因此在这里进行了整理&#xff0c;分享给有需要的朋友。今天主要是说一下区域选择这项功能&#xff0c;Qt自带的表格控件是具有区域选择功能的&#xff0c;但是他并…
阅读更多...
【Linux技术专题系列】「必备基础知识」一起探索（su、sudo等相关身份提权/身份切换机制）

【Linux技术专题系列】「必备基础知识」一起探索（su、sudo等相关身份提权/身份切换机制）

内容简介 Linux技术专题&#xff0c;主要介绍相关&#xff0c;针对于Linux开发和知识体系的必备开发技能以及基础常识&#xff0c;是开发者必备的知识体系和方法论。 什么是用户、用户组 Linux用户 Linux系统是一个多用户多任务的分时操作系统&#xff0c;任何一个要使用系统资…
阅读更多...
如何制作mp3音频文件？分享制作mp3的简单方法

如何制作mp3音频文件？分享制作mp3的简单方法

MP3 对每个人来说都不是一个陌生的名字&#xff0c;因为它是全球排名第一的主流音乐格式。听过上千首MP3歌曲&#xff0c;你知道自己可以制作MP3文件吗&#xff1f;如果答案是否定的&#xff0c;那么您很幸运能找到这篇文章&#xff0c;因为它将通过向您介绍一个免费且简单的解…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023