一算法简介

1）算法案例引入

2）算法思想

3）算法概念

4）算法求解的问题的特征

5）算法应用

二算法常见问题

1）活动安排问题（区间调度问题）

今年暑假不AC

2）区间覆盖问题

3）最优装载问题

4）多机调度问题

三算法典型应用

Huffman编码

如何找最优编码方案？

贪心过程

模拟退火

模拟退火算法：贪心+概率

模拟退火算法的主要步骤

模拟退火在算法竞赛中的典型应用

算法实践：

1）函数最值问题

模拟退火算法的缺点

2）最小圆覆盖

爬山法

A*搜索

附录：

一算法简介

1）算法案例引入

硬币问题

某人带着3种面值的硬币去购物，有1元、2元、5元的，硬币数量不限；

他需要支付M元，问怎么支付，才能使硬币数量最少？

代码：

#include <iostream>
using namespace std;
#define NUM 3
const int Value[NUM] = {5, 2, 1};
int main(){  
    int i, money;
    int ans[NUM]={0};
    cout << "输入总钱数：";
    cin >> money;
    for(i= 0; i < NUM; i++){       //求每种硬币的数量
        ans[i] = money/Value[i];
        money = money - ans[i]*Value[i];
    }
    for(i= 0; i < NUM; i++)
        cout<<Value[i]<<"元硬币数："<<ans[i]<<endl;
    return 0;
}

虽然每一步选硬币的操作，并没有从整体最优来考虑，而是只在当前步骤选取了局部最优，但是结果是全局最优的。

然而，局部最优并不总是能导致全局最优。

硬币问题，用贪心法，一定能得到最优解吗？

在硬币问题中，如果改换一下参数，就不一定能得到最优解。例如：硬币面值比较奇怪，是1、2、4、5、6元，支付9元，如果用贪心法，答案是6 + 2 + 1，需要3个硬币，而最优的5 + 4只需要2个硬币。

所以，在硬币问题中，用贪心法是否能得到最优，跟硬币的面值有关。如果是1、2、5这样的面值，贪心是有效的，而对于1、2、4、5、6这样的面值，贪心是无效的。

任意面值硬币问题的求解：动态规划。

2）算法思想

看一步走一步，而且只看一步；

在每一步，选当前最优的；

不回头，不改变已有的选择；

3）算法概念

把整个问题分解成多个步骤，在每个步骤都选取当前步骤的最优方案，直到所有步骤结束；在每一步都不考虑对后续步骤的影响，在后续步骤中也不再回头改变前面的选择。简单来说就是走一步看一步。

贪心法在解决问题的策略上目光短浅，只根据当前已有的信息就做出选择，而且一旦做出了选择，不管将来有什么结果，这个选择都不会改变。换言之，贪心法并不是从整体最优考虑，它所做出的选择只是在某种意义上的局部最优。

这种局部最优选择并不总能获得整体最优解，但通常能获得近似最优解。

4）算法求解的问题的特征

（1）最优子结构性质

当一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构性质，也称此问题满足最优性原理。

（2）贪心选择性质

所谓贪心选择性质是指问题的整体最优解可以通过一系列局部最优的选择，即贪心选择来得到。

贪心算法没有固定的算法框架，关键是如何选择贪心策略。贪心策略必须具备无后效性，即某个状态以后的过程不会影响到以前的状态，只与当前状态有关。

动态规划法通常以自底向上的方式求解各个子问题，而贪心法则通常以自顶向下的方式做出一系列的贪心选择。

5）算法应用

例如图论中的最小生成树算法，单源最短路径算法，Dijkstra算法

二算法常见问题

1）活动安排问题（区间调度问题）

今年暑假不AC

题目描述：

有很多电视节目，给出它们的起止时间。有些节目时间冲突。问能完整看完的电视节目最多有多少？

题目分析：

解题的关键在于选择什么贪心策略，才能安排尽量多的活动。由于活动有开始时间和结束时间，考虑三种贪心策略：

（1）最早开始时间。

（2）最早结束时间。

（3）用时最少。

分析三种贪心策略：

（1）最早开始时间：错误，因为如果一个活动迟迟不终止，后面的活动就无法开始。

（2）最早结束时间：合理，一个尽快终止的活动，可以容纳更多的后续活动。

（3）用时最少：错误。

对最早结束时间进行贪心，算法步骤如下：

1）把n个活动按结束时间排序

2）选择第一个介绍的活动，并删除与他时间相冲突的活动

3）重复步骤二，直到活动为空，每次选择剩下的活动中最早结束的那个活动，并删除与他时间冲突的活动。

分析上述贪心算法是否保证得到全局最优解：

1）符合最优子结构性质，选中的第一个活动，她一定在某个最优解中；同理，选中的第二个，第三个等也都在这个最优解中。

2）附和贪心选择性质。算法的每一步都使用了相同的贪心策略

代码：

struct node{
	int  start,endl
}record[maxn];
int cmp (const node&a,const node &b)
{
	return a.end<b.end;
}
for(i=0;i<n;i++)
	scanf("%d %d",&record[i].start,&record[i].endl);
qsort(record,n,sizeof(record,cmp));//按结束时间排序 
int count;
int lastend=-1;
for(i=0;i<n;i++)
{
	if(record[i].start>=lastend)//后一个起始时间大于等于前一个终止时间 
	{
		count++;
		lasted=record[i].end;//记录前一个活动的终止时间 
	}
}
printf("%d",count);

2）区间覆盖问题

题目描述：

给定一个长度为n的区间，再给出m条线段的左端点（起点）和右端点（终点）。问最少用多少条线段可以将整个区间完全覆盖。

题目分析：

贪心：尽量找出更长的线段。

解题步骤是：

（1）把每个线段按照左端点递增排序。

（2）设已经覆盖的区间是[L, R]，在剩下的线段中，找所有左端点小于等于R，且右端点最大的线段，把这个线段加入到已覆盖区间里，并更新已覆盖区间的[L, R]值。

（3）重复步骤（2），直到区间全部覆盖

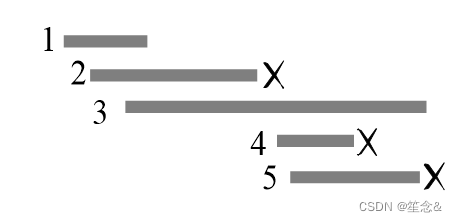
3）最优装载问题

题目描述：

有n种药水，体积都是V，浓度不同。把它们混合起来，得到浓度不大于w%的药水。问怎么混合，才能得到最大体积的药水？注意一种药水要么全用，要么都不用，不能只取一部分。

题目分析：

要求配置浓度不大于w%的药水，贪心思路：尽量找浓度小的药水。

先对药水按浓度从小到大排序，药水的浓度不大于w%就加入，如果药水的浓度大于w%，计算混合后总浓度，不大于w%就加入，否则结束判断。

4）多机调度问题

题目描述：

有n个独立的作业，由m台相同的机器进行加工。

作业i的处理时间为ti，每个作业可在任何一台机器上加工处理，但不能间断、拆分。

要求给出一种作业调度方案，在尽可能短的时间内，由m台机器加工处理完成这n个作业。

题目分析：

贪心策略：最长处理时间的作业优先，即把处理时间最长的作业分配给最先空闲的机器。让处理时间长的作业得到优先处理，从而在整体上获得尽可能短的处理时间。

1）如果n<=m，需要的时间就是n个作业当中最长的处理时间

2）如果n>m，首先将n个作业按处理时间从大到小排序，然后按顺序把作业分配给空闲的计算机

三算法典型应用

Huffman编码

Huffman编码是贪心思想的典型应用，是一个很有用的、很著名的算法。Huffman编码是“前缀”最优编码

例：给出一段字符串，它只包含A、B、C、D、E这5种字符。字符出现频率不同。

简单编码：

每个字符用3位二进制数表示，存储的总长度是：3*(3+9+6+15+19) = 156。

变长编码：出现次数多的字符用短码表示，出现少的用长码表示。

存储的总长度是：3*4 + 9*3 + 6*4 + 15*2 + 19*1 = 112。

第二种方法相当于对第一种方法，压缩比是：156/112=1.39。

编码算法的基本要求：编码后得到的二进制串，能唯一地进行解码还原。

第一种方法是正确的，每3位二进制数对应一个字符。

第二种方法，也是正确的，

例如"1100 111 10 0 1101"，

解码后唯一得到"ABDEC"。

胡乱设定编码方案，很可能错误，例如：

编码无法解码还原。例如"100"，是"A"、"BE"还是"DEE"呢？

错误的原因是，某个编码是另一个编码的前缀(prefix)，即这两个编码有包含关系，导致了混淆

如何找最优编码方案？

有没有比第二种编码方法更好的方法？

这引出了一个字符串存储的常见问题：给定一个字符串，如何编码，能使得编码后的总长度最小？即如何得到一个最优解？

Huffman编码是前缀编码算法中的最优算法。

Huffman编码是利用贪心思想构造二叉编码树的算法。

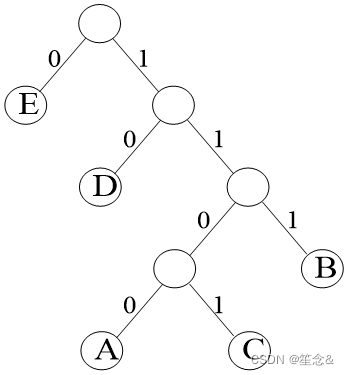
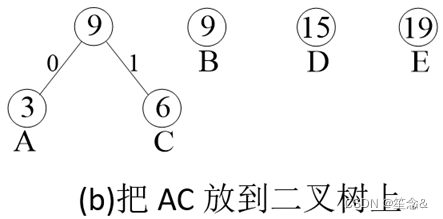
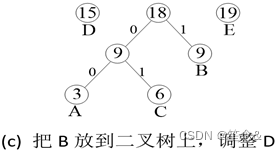
贪心过程

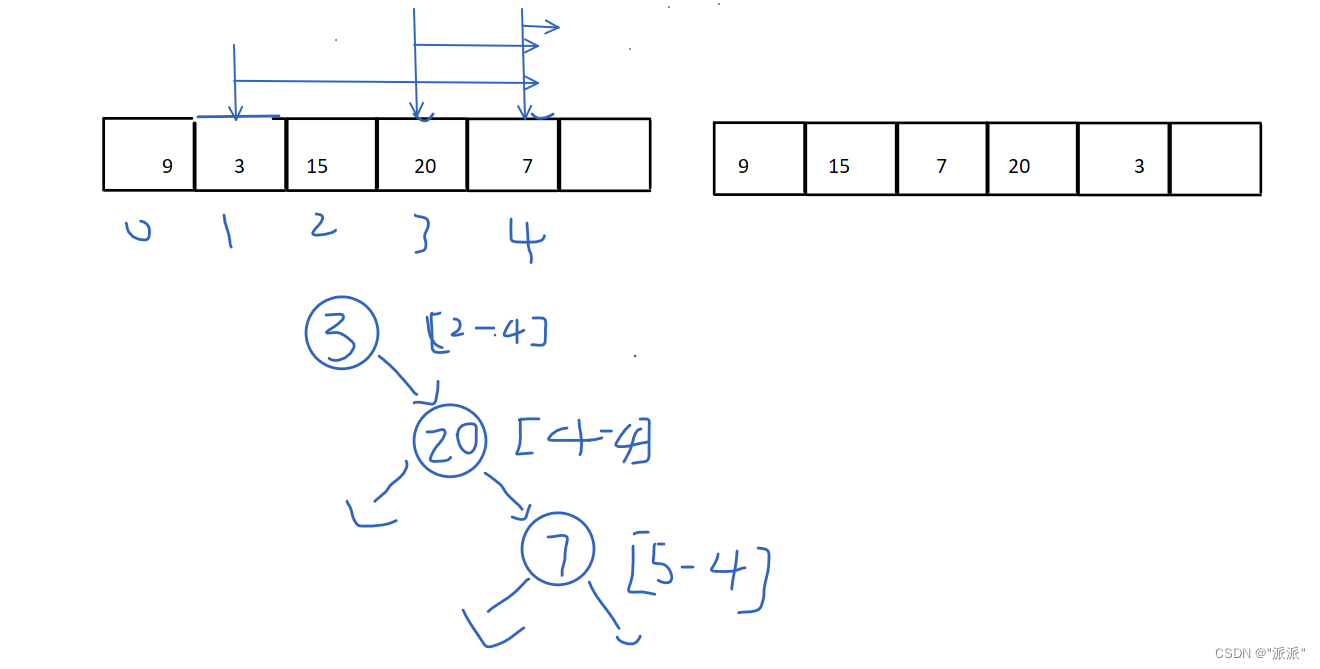
对所有字符按频次排序：

从最少的字符开始，用贪心思想安排在二叉树上。

例题：

输入一个字符串，分别用普通ASCII编码（每个字符8bit）和huffman编码，输出编码后的长度，并输出压缩比。

Sample Input：

AAAAABCD

Sample Output：

64 13 4.9

分析：

这一题正常的解题过程是：

首先统计字符出现的频次，

然后用huffman算法编码，

最后计算编码后的总长度。

不过，由于只需要输出编码总长度，而不要求输出每个字符的编码，所以可以跳过编码过程，利用上图所描述的huffman编码思想（圆圈内的数字是出现频次），直接计算编码的总长度

模拟退火

模拟退火算法基于这样一个物理原理：

一个高温物体降温到常温，温度越高时，降温的概率越大（降温更快），温度越低降温概率越小（降温更慢）。

模拟退火算法利用这样一种思想进行搜索，即进行多次降温（迭代），直到获得一个可行解

模拟退火算法：贪心+概率

下图中，A是局部最高点，B是全局最高点。

普通的贪心算法，如果当前状态在A附近，会一直爬山，最后停在局部最高点A，无法到达B。

模拟退火算法能跳出A，得到B。因为它不仅往上爬山，而且以一定概率接受比当前点更低的点，使程序有机会摆脱局部最优而到达全局最优。这个概率会随时间不断减小，从而最后能限制在最优解附近。

模拟退火算法的主要步骤

（1）设置一个初始的温度T。

（2）温度下降，状态转移。从当前温度，按降温系数下降到下一个温度。在新的温度，计算当前状态。

（3）如果温度降到设定的温度下界，程序停止。

伪代码如下：

eps = 1e-8;          //终止温度，接近于0，用于控制精度
T = 100;           //初始温度，应该是高温，以100度为例
delta = 0.98;     //降温系数，控制退火的快慢，小于1
g(x);            //状态x时的评价函数，例如物理意义上的能量
now, next;         //当前状态和新状态
while(T > eps){             //如果温度未降到eps
		g(next), g(now);      //计算能量。
		dE= g(next)-g(now);  //能量差
		if(dE >= 0)            //新状态更优，接受新状态
			now = next;
		else if(exp(dE/T)> rand()) 
                                  //如果新状态更差，在一定概率下接受它，e^(dE/T)
			now = next;
		T *= delta;          //降温，模拟退火过程
}

模拟退火在算法竞赛中的典型应用

函数最值问题

TSP旅行商问题

最小圆覆盖

最小球覆盖

算法实践：

1）函数最值问题

Strange fuction

函数F(x) = 6 * x^7+8*x^6+7*x^3+5*x^2-y*x

其中x的范围是0 <= x <=100。

输入y值，输出F(x)的最小值。

#include <bits/stdc++.h>
using namespace std;
const double eps = 1e-8;     //终止温度
double y;
double func(double x){       //计算函数值
	return 6*pow(x,7.0)+8*pow(x,6.0)+7*pow(x,3.0)+5*pow(x,2.0)-y*x;
}
double solve(){
  	double T = 100;         //初始温度
  	double delta = 0.98;   //降温系数
  	double x = 50.0;        //x的初始值
  	double now = func(x);  //计算初始函数值
  	double ans = now;       //返回值
  	while(T > eps){         //eps是终止温度
     	int f[2]={1,-1};
		double newx = x+f[rand()%2]*T;    //按概率改变x，随T的降温而减少
		if(newx >= 0 && newx <= 100){
	 		double next = func(newx);
			ans = min(ans,next);
			if(now - next > eps){x = newx; now = next;}     //更新x
		}
		T *= delta;
	}
    return ans;
}
int main(){
     int cas; scanf("%d",&cas);
	 while(cas--){
		scanf("%lf",&y);
		printf("%.4f\n",solve());
	}
}

模拟退火算法的缺点

模拟退火算法用起来非常简单方便，不过也有缺点。

它得到的是一个可行解，而不是精确解。

例如上面的例题，计算到4位小数点的精度就停止，实际上是一个可行解，所以算法的效率和要求的精度有关。

一般情况下，模拟退火算法的复杂度会比其它精确算法差。应用时需要仔细选择初始温度T、降温系数delta、终止温度eps等。

2）最小圆覆盖

给定n个点的平面坐标，求一个半径最小的圆，把n个点全部包围，部分点在圆上。

两点定圆或三点定圆

输入n个点的坐标，n < 500，求最小圆覆盖。

下面用模拟退火编程。

#include <bits/stdc++.h>
using namespace std;
#define eps 1e-8
const int maxn = 505;
int sgn(double x){
    if(fabs(x) < eps)  return 0;
    else return x<0?-1:1;
}
struct Point{
    double x, y;
};
double Distance(Point A, Point B){return hypot(A.x-B.x,A.y-B.y);}
//求三角形abc的外接圆的圆心：
Point circle_center(const Point a, const Point b, const Point c){
    Point center;
    double a1=b.x-a.x, b1=b.y-a.y, c1=(a1*a1+b1*b1)/2;
    double a2=c.x-a.x, b2=c.y-a.y, c2=(a2*a2+b2*b2)/2;
    double d =a1*b2-a2*b1;
    center.x =a.x+(c1*b2-c2*b1)/d;
    center.y =a.y+(a1*c2-a2*c1)/d;
    return center;
}
//求最小覆盖圆，返回圆心c，半径r：
void min_cover_circle(Point *p, int n, Point &c, double &r){
    double T = 100.0;      //初始温度
    double delta = 0.98;  //降温系数
    c = p[0];
    int pos;
    while (T > eps){       //eps是终止温度
        pos = 0; r=0;       //初始： p[0]是圆心，半径是0
        for(int i = 0; i <= n - 1; i++)  //找距圆心最远的点
            if (Distance(c, p[i]) > r){
                r = Distance(c, p[i]);     //距圆心最远的点，肯定在圆周上
                pos = i;
            }
        c.x += (p[pos].x - c.x) / r * T;  //逼近最后的解
        c.y += (p[pos].y - c.y) / r * T;
        T *= delta;
    }
}

int main(){
    int n;                //点的个数
    Point p[maxn];      //输入点
    Point c; double r;  //最小覆盖圆的圆心和半径
    while(~scanf("%d",&n) && n){
        for(int i=0;i<n;i++) scanf("%lf %lf",&p[i].x,&p[i].y);
        min_cover_circle(p,n,c,r);
        printf("%.2f %.2f %.2f\n",c.x,c.y,r);
    }
    return 0;
}

另外两种就不赘述，后续会介绍