网络结构

卷积层+池化层+全连接层

输入$448\ast 448$大小的图片
输出$7\ast 7\ast 30$的张量

30维张量包括20个对象的概率，2个bounding box的置信度及其位置（一个bounding box位置信息需要四个值，两个bounding box总需要8个值）

20个对象的概率即为条件概率，如果该网格中存在一个检测对象，那么该检测对象为类别A的概率：$p(P_A|exist\_objects)$

2个bounding box的置信度，其中置信度=p(exist_objects) * 该预测的bounding box与该对象的真实边框的IOU值

两个bounding box的置信度分别于20个类别的概率相乘，可得到分在在两个bounding box中的每一类的概率。

重点分析

bounding box相关内容

每一个网格给出两个bounding box信息，但一个对象只需要一个bounding box。为此，通过一定的个标准进行舍取。
输出的30维向量中，包含两个bounding box的置信度，该置信度反应出预测框与真实框IOU交并比。那么两个框IOU交并比，谁大就由谁负责预测一个对象，并且$p(exist\_objects)$为1，另一个bounding box的$p(exist\_objects)$为0。那么根据公式可知置信度其实就为IOU交并比值。

grid cell 与 bounding box

将图片分成$7\ast 7$的网格（grid cell）,每一个grid cell生成两个预测框bounding box，该预测框的中心点都落在该grid cell格子内部。每一个grid cell只能预测一个物体。

损失函数

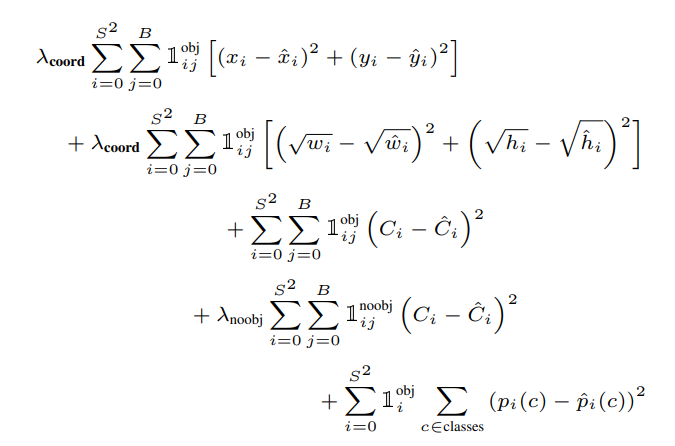
公式分析，其中$1_i^{obj}$表示网格$i$存在检测对象，$1_{ij}^{obj}$表示网格$i$的第$j$个bounding box存在检测对象，$1_{ij}^{nobj}$表示网格$i$的第$j$个bounding box不存在检测对象

第一行表示边框中心点的误差，grid cell中负责预测的bounding box框与真实框的误差

第二行表示预测框相对于真实框的宽和高的误差。其中开方旨在降低因为大小不同带来的敏感问题

第三行表示置信度误差，即边框内存在对象，$\overline{C_i}$越高越好

第四行也表示置信度误差，即边框内不存在对象，$\overline{C_i}$越低越好

最后一行表示对象分类误差