目录
二叉数遍历迭代法
1.1前序遍历
1.2中序遍历
1.3后续遍历
二叉树最小深度
二叉树所有路径
中序后序构造二叉树
验证二叉搜素树
二叉数遍历迭代法
1.1前序遍历
前序遍历顺序:根—左—右;
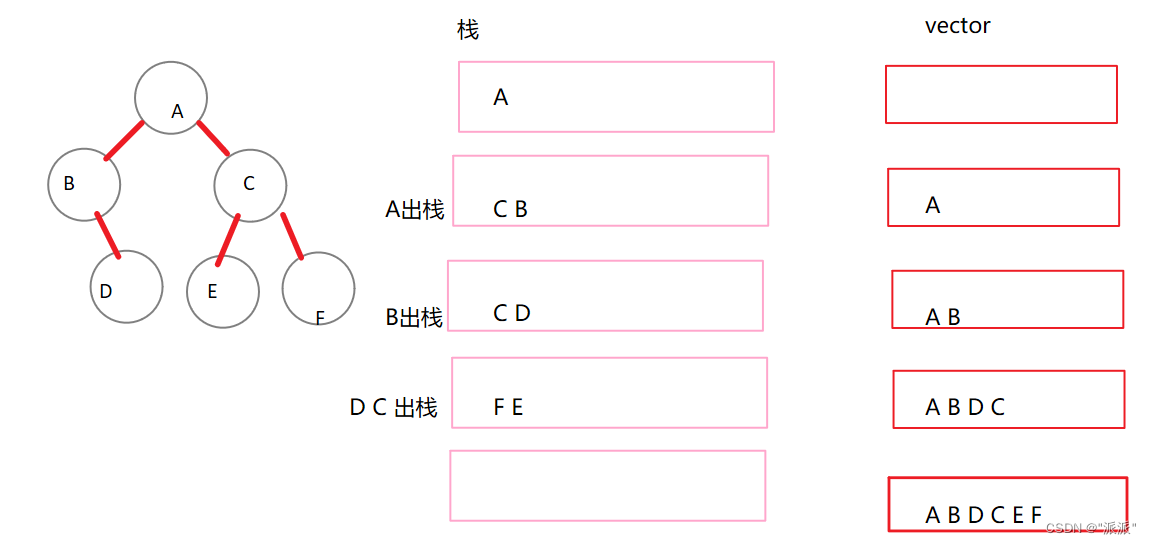
解法1:用栈来进行中间过程处理,结果存入vector中
思路:每次先处理中间的结点,先将根结点入栈,再将右孩子入栈,左孩子入栈。每次从栈顶拿数据,重复操作。
代码演示:
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
stack<TreeNode*> st;
vector<int> result;
if (root == NULL) return result;
st.push(root);
while (!st.empty())
{
TreeNode* node = st.top();
st.pop();
result.push_back(node->val);
if (node->right) st.push(node->right);
if (node->left) st.push(node->left);
}
return result;
}
};
解法2:中序遍历是先访问根结点,然后访问左子树。
我们可以直接把先访问的根结点直接存入vector中,然后去遍历它的左子树。重复上一次操作。当它的左子树为空时,则去遍历它的右子树。(右子树也按之前的方法,不为空则直接放入vector中,后去遍历它的左子树) 其中要把遍历过的结点放入栈中,当它的左子树为空时,栈顶元素就是该子树的根结点,可通过它去找到右子树,若其右子树也为空,也一样可以通过栈顶元素去找右子树。(访问栈顶元素后要将其出栈)

代码演示:
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
stack<TreeNode*> s;
vector<int> v;
TreeNode*cur=root;
while(cur||!s.empty())
{
while(cur)
{
s.push(cur);
v.push_back(cur->val);
cur=cur->left;
}
TreeNode* top=s.top();
s.pop();
cur=top->right;
}
return v;
}
};1.2中序遍历
中序遍历顺序:左—根—右
思路:与上面前序遍历的解法2类似,但由于访问左子树先于根结点,所以访问左子树时只需把其入栈,不用放入vector中,当其左子树为空时,那么此时栈中最后的元素可当作左结点,将其放入vector中,后通过栈顶元素找到其右子树,(把栈顶元素出栈),以同样的方法去遍历右子树。
代码实现:
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> v;
stack<TreeNode*> s;
TreeNode*cur=root;
while(cur||!s.empty())
{
while(cur)
{
s.push(cur);
cur=cur->left;
}
TreeNode* top=s.top();//其左子树为空
s.pop();
v.push_back(top->val);
cur=top->right; //去找右子树,以同样方法遍历右子树
}
return v;
}
};1.3后续遍历
后续遍历顺序:左—右—根
解法1:与前序遍历解法一类似,只要把入栈顺序更改下,再将放入vector中的数据反转一下即可。
代码实现:
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
stack<TreeNode*> st;
vector<int> result;
if (root == NULL)
return result;
st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
st.pop();
result.push_back(node->val);
if (node->left) st.push(node->left);
if (node->right) st.push(node->right);
}
reverse(result.begin(), result.end());
return result;
}
};
解法2:
与中序遍历解法类似,不过后序遍历的访问顺序是右子树先于根结点。
当cur一直往后遍历时,当其左子树为空时,此时栈中最后一个元素当成是根结点,此时有两种情况。
1.那个根结点的右子树为空,那么将根结点当成子树的左孩子,将其放入vector中,并将其出栈。
2.那个根结点此时右子树不为空,则以同样的方法遍历该根结点的右孩子。当遍历完返回后,回到这个根结点时,又会去遍历它的右子树,所以需要记录该根结点的右子树(不为空时)是否被访问过。

代码实现:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> v;
stack<TreeNode*> s;
TreeNode*cur=root;
TreeNode* pre;
while(cur||!s.empty())
{
while(cur)
{
s.push(cur);
cur=cur->left;
}
TreeNode* top=s.top();
if(top->right==nullptr||top->right==pre)//右子树为空或则已近访问过了
{
v.push_back(top->val);
s.pop();
pre=top;
}
else
{
cur=top->right;
}
}
return v;
}二叉树最小深度
最小深度是指根节点到最近叶子节点的最短路径上的节点数量
题目描述
class Solution {
public:
int minDepth(TreeNode* root) {
if(root==nullptr)
return 0;
int lefti=minDepth(root->left);
int righti=minDepth(root->right);
if(root->left==nullptr&&root->right!=nullptr)
lefti=righti;
if(root->right==nullptr&&root->left!=nullptr)
righti=lefti;
return 1+min(lefti,righti);
}
};迭代:
class Solution {
public:
int minDepth(TreeNode* root) {
if(root==nullptr)
return 0;
queue<TreeNode*> _q;
_q.push(root);
int count=0;
while(!_q.empty())
{
int size=_q.size();
count++;
int flag=0;
while(size--)
{
TreeNode* cur=_q.front();
_q.pop();
if(cur->left==nullptr&&cur->right==nullptr)
{
return count;
}
if(cur->left!=nullptr)
_q.push(cur->left);
if(cur->right!=nullptr)
_q.push(cur->right);
}
}
return count;
}
};二叉树所有路径
题目描述
代码:解法1
深度优先搜索
如果当前节点不是叶子节点,则在当前的路径末尾添加该节点,并继续递归遍历该节点的每一个孩子节点。
如果当前节点是叶子节点,则在当前路径末尾添加该节点后我们就得到了一条从根节点到叶子节点的路径,将该路径加入到答案即可。
class Solution {
public:
void _binary(string s,vector<string>& v,TreeNode* root)
{
if(root!=nullptr)
s+=to_string(root->val);
if(root->left==nullptr&&root->right==nullptr)
{
v.push_back(s);
return;
}
if(root->left)
_binary(s+"->",v,root->left);
if(root->right)
_binary(s+"->",v,root->right);
}
vector<string> binaryTreePaths(TreeNode* root) {
string str;
vector<string> v;
_binary(str,v,root);
return v;
}
};解法2:与解法1类似,用广度优先搜索来实现。不过用到了队列来辅助,来记录遍历的节点。其中结点值与->是成对出现的。 pair<TreeNode*,string> p(root,"")一起进行出入队列操作。每一个结点值有它对应的路劲,
class Solution {
public:
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> v;
queue< pair<TreeNode*,string> > q;
pair<TreeNode*,string> p(root,"");
q.push(p);
while(!q.empty())
{
string path = q.front().second ;
root = q.front().first;
q.pop();
path += to_string(root->val);
if(!root->left && !root->right)
{
v.push_back(path);
continue;
}
path += "->";
if(root->left)
{
p = {root->left,path};
q.push(p);
}
if(root->right)
{
p = {root->right,path};
q.push(p);
}
}
return v;
}
};相关题型:力扣112,113
中序后序构造二叉树
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
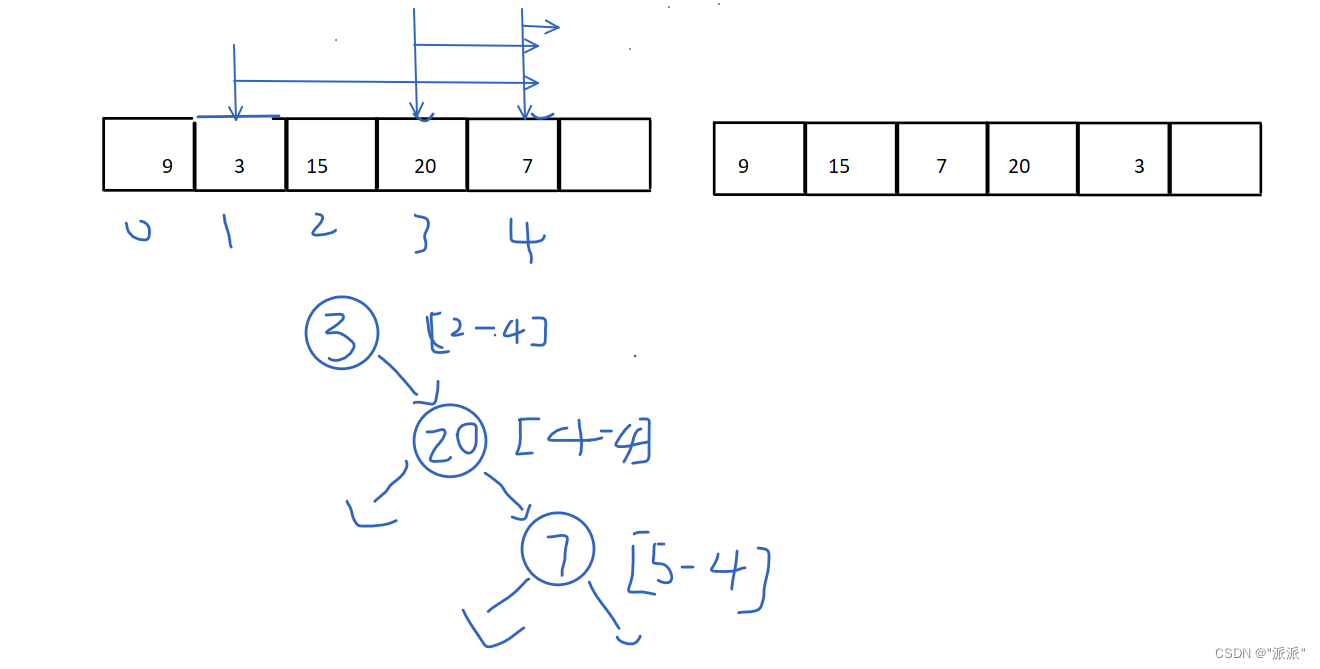
通过postorder数组最后面的元素,可以找到根结点,后面在inorder 数组里面找到该元素,在中序遍历的数组里,该元素前面的就是它的左子树,后面的是它的右子树。先找它的右子树,因为在inorder 数组里面元素顺序是左-右-根,离根结点近的是右子树。
代码:
class Solution {
public:
TreeNode* _bulidTree(vector<int>& inorder, vector<int>& postorder,
int& pre, int begin, int end)
{
if (begin > end)
return nullptr;
TreeNode* root = new TreeNode(postorder[pre]);
pre--;
int rooti = begin;
while (rooti <= end)
{
if (root->val == inorder[rooti])
break;
else
rooti++;
}
root->right = _bulidTree(inorder, postorder, pre, rooti + 1, end);
root->left = _bulidTree(inorder, postorder, pre, begin, rooti - 1);
return root;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
int begin, end, pre;
begin = 0;
end = pre = postorder.size() - 1;
return _bulidTree(inorder, postorder, pre, begin, end);
}
};相关题型:105
验证二叉搜素树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
解法1:根据二叉搜书树的性质,对其进行后续遍历,若是二叉搜索树,则后续遍历的结果是完全升序的。
解法2:与上面介绍的后序遍历第二种思路相似,要用一个变量去记录之上一个结点。
class Solution {
public:
bool isValidBST(TreeNode* root) {
stack<TreeNode*> st;
TreeNode* cur = root;
TreeNode* pre = NULL; // 记录前一个节点
while (cur != NULL || !st.empty()) {
while (cur)
{
st.push(cur);
cur = cur->left; // 左
}
cur = st.top(); // 中
st.pop();
if (pre != NULL && cur->val <= pre->val)
return false;
pre = cur; //保存前一个访问的结点
cur = cur->right; // 右
}
return true;
}
};相关题型:力扣530




![[思维模式-14]:《复盘》-2- “知”篇 - 复盘之道](https://img-blog.csdnimg.cn/d6f56334e34b49ffb508aa30c0e12337.png)






![[思维模式-13]:《复盘》-1- “知”篇 - 认识复盘](https://img-blog.csdnimg.cn/08f31da6b7904e6f9ee678d9c24c5f74.png)



