函数

形参不需要定义var，函数可以付给一个变量
函数就可以看作一个值，值就要用变量来指向。
function在一行的开头时，表达的是函数声明语句，而不是表达式，所以没有求值结果
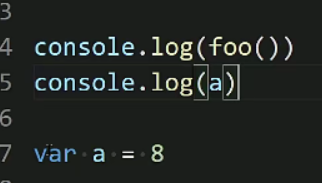
使用函数声明形式创建的函数function(){ } 它会在所有的代码执行之前就被创建，所以我们在可以函数声明前调用函数，使用函数表达式创建函数不会被声明提前。
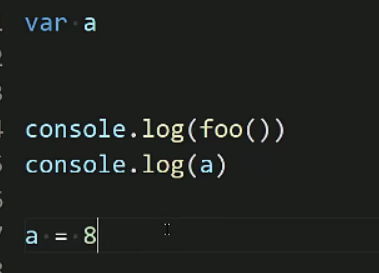
var的定义也可以实现提前，下面的打印的a是undefined，下面这个会将a的定义提前，但是赋值还是在原来的位置
下面就出现了let变量，let变量在定义前是不能被使用的，定义前的这部分区域也就叫做TDZ（temper dead zone暂时性死区），并且let定义的变量不能重复定义，第三let可以解决闭包问题。
1.let定义的变量在块级作用域内，var是在函数作用域2.let定义的变量不能重复定义（在控制台两次粘贴可以）3.let定义的变量没有将定义提升，但有TDZ行为，即该作用域内定义完成之前不能使用该变量

在这里插入图片描述

作用域

函数中的变量每次调用都会重新创建，定义在任意函数之外的变量称为全局变量(全局作用域)，如果在函数中没有用var定义变量，并且全局变量中有一个x，那么就是使用的全局变量的x。
定义在函数中的变量叫做局部作用域
函数还可以在其他函数中定义，这样就会产生多层次的局部作用域

全局作用域自动存在
其他作用域都是通过函数的运行产生的
函数不运行，是不会产生作用域的
函数运行多次，会产生多个作用域
函数运行完后，作用域往往会销毁掉(闭包)

例子

<script>
  //接受一个n，判断它是否是素数
  var isPrime = function (n) {
    for (var i = 2; i <= Math.sqrt(n); i++) {
      if (n % i == 0) {
        return false
      }
    }
    return true
  }
</script>

<script>
  //判断十进制数字的位数
  debugger
  var digitWidth = function (n) {
    var c = 0
    do {
      var digit = n % 10
      c++
      n = (n - digit) / 10
    } while (n > 0)
    return c
  }
  console.log(digitWidth(10))
</script>

<script>
  var chessBoard = function (size) {
    var a = ''
    var b = ''
    for (var i = 0; i < size; i++) {
      if (i % 2) {
        a += ' '
        b += '#'
      } else {
        a += '#'
        b += ' '
      }
    }
    var result = ''
    for (var i = 0; i < size; i++) {
      if (i % 2) {
        result += a
      } else {
        result += b
      }
      result += '\n'
    }
    return result
  }
  console.log(chessBoard(8))
</script>

这道题注意if括号里的顺序问题

<script>
  var fizzBuzz = function (n) {
    for (var i = 1; i < n; i++) {
      if (i % 3 == 0 && i % 5 == 0) {
        console.log('fizz buzz')
      } else if (i % 5 == 0) {
        console.log('buzz')
      } else if (i % 3 == 0) {
        console.log('fizz')
      } else {
        console.log(i)
      }
    }
  }
</script>

<script>
  //求一个正数的平方根(二分法)
  function sqrt(n) {
    var l = 0
    var r = n
    while (r - l > 0.000001) {
      var m = (l + r) / 2
      if (m * m == n) {
        return m
      } else if (m * m < n) {
        l = m
      } else if (m * m > n) {
        r = m
      }
    }
    return (l + r) / 2
  }
</script>

<script>
  //判断一个数是不是水仙花数
  function digitWidth(n) {
    var width = 0
    do {
      var digit = n % 10
      n = (n - digit) / 10
      width++
    } while (n > 0)
    return width
  }
  function power(x, n) {
    var exp = 1
    for (var i = 0; i < n; i++) {
      exp *= x
    }
    return exp
  }
  function isNarcissistic(n) {
    var width = digitWidth(n)
    var m = n
    var sum = 0

    do {
      var digit = m % 10
      sum += power(digit, width)
      m = (m - digit) / 10
    } while (m > 0)

    if (sum == n) {
      return true
    } else {
      return false
    }
  }

  for (var i = 1; i < 10000; i++) {
    if (isNarcissistic(i)) {
      console.log(i)
    }
  }
</script>

<script>
  //判断一个数是否是回文数字
  function isPalindrow(n) {
    var m = n
    var revert = 0
    while (m > 0) {
      var digit = m % 10
      revert = revert * 10 + digit
      m = (m - digit) / 10
    }
    if (revert == n) {
      return true
    } else {
      return false
    }
  }
</script>

<script>
  //判断一个数是否是完全数(一个数等于因式之和)
  function isCompleteNumber(n) {
    var sum = 1
    for (var i = 2; i <= Math.sqrt(n); i++) {
      if (n % i == 0) {
        var j = n / i
        if (i == j) {
          sum += i
        } else {
          sum += i + j
        }
      }
    }
    return n == sum
  }
</script>

调用栈

栈是后进先出
调用栈的两个语义：1.计算机内部用于存储函数返回位置，函数的局部变量的内存空间，叫做调用栈。2.函数间的相互调用的等待关系，叫调用栈

可选参数

如果函数参数少写了一个实参，那么那个实参就式undefined类型，浏览器就自动补全另一个参数

<script>
  function a() {
    console.log(arguments[0], arguments[5])
  }
  a(1, 2, 3, 4, 5, 6, 7, 8, 9)
</script>

通过arguments可以取出函数参数的值，arguments就看作一个数组即可
js还可以设置参数的默认值，这样在调用函数的时候可以使用默认参数

<script>
  function power(a, n = 2) {
    var result = 1
    for (var i = 1; i <= n; i++) {
      result *= a
    }
    return result
  }

  console.log(power(3))
</script>

闭包

一直没有销毁的作用域我们就叫做闭包，在js中返回一个函数，函数内用到了外层函数的变量，所以内层函数在，外层函数的变量就在，这样作用域就不会被销毁，形成了闭包

<script>
  debugger
  function wrapValue(n) {
    var localVariable = n;
    function get(){
      return localVariable
    }
    return get
  }

  var wrap1 = wrapValue(1)
  var wrap2 = wrapValue(2)
  console.log(wrap1())
  console.log(wrap2())
</script>

递归

结束条件，在该条件中，不递归
调用自己的时候认为自己已经被正确实现了，问题的更小规模可以直接调用自己求解
调用自身的时候一定要传入更小规模的参数/或者是更接近非递归条件的参数

<script>
  //输入n个数并倒叙输出：输入1个数a；输入n-1个数并倒叙输出；输出a
  function inputAndReverseOutput(n){
    if(n == 0){
      return
    }
    var a = prompt()
    inputAndReverseOutput(n-1)
    console.log(a)
  }
</script>

<script>
  //斐波那契额数列
  function fibonacci(n) {
    if (n == 1 || n == 2) {
      return 1
    } else {
      return fibonacci(n - 1) + fibonacci(n - 2)
    }
  }
  var n = Number(prompt())
  for (var i = 1; i <= n; i++) {
    console.log(fibonacci(i))
  }
</script>

<script>
  //汉诺塔,将放置于start位的顶部的n个盘移动到end位
  function hanoi(n, start, end) {
    if (n == 1) {
      console.log(start, '->', end)
      return
    }
    var mid = 6 - start - end//计算出中转位的编号
    hanoi(n - 1, start, mid)//将摆放在起点位置顶部的n-1个盘移到中转位上
    console.log(start, '->', end)//将摆放在起点位置唯一的一个盘移到终点位上
    haooi(n - 1, mid, end)//将摆放在中转位顶部的n-1个盘移到终点位上
  }
</script>