216. 组合总和 III

news2024/11/18 15:45:03

216. 组合总和 III

找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

只使用数字1到9
每个数字 最多使用一次

返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

示例 1:

输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。

示例 2:

输入: k = 3, n = 9
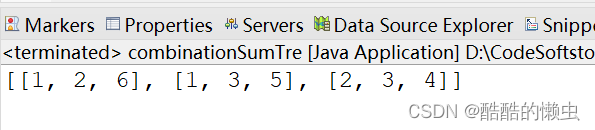
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。

示例 3:

输入: k = 4, n = 1
输出: []
解释: 不存在有效的组合。
在[1,9]范围内使用4个不同的数字，我们可以得到的最小和是1+2+3+4 = 10，因为10 > 1，没有有效的组合。

提示:

2 <= k <= 9
1 <= n <= 60

思路：（回溯）

注意点：

找到 k 个数相加的和为 n ，所以返回结果要同时满足以下条件：n == 0 && k == 0；
界限判断及剪枝：
- 当 k == 0 时说明还可以在加 0 个数，此前结果不为 n ，返回；
- 当最小的 k 个数相加都大于 n ，肯定找不到有效组合，返回。

代码：(Java)

import java.util.ArrayList;
import java.util.List;

public class combinationSumTre {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		int k = 3;
		int n = 9;
		System.out.println(combinationSum3(k,n));

	}
	public static List<List<Integer>> combinationSum3(int k, int n) {
		List<List<Integer>> combinations = new ArrayList<>();
		List<Integer> combination = new ArrayList<>();
		if(((1 + k) * k / 2) > n || n > 45){
			return combinations;
		}
		backtracking(combinations, combination, 1, k ,n);
		return combinations;
    }
	private static void backtracking(List<List<Integer>> combinations, List<Integer> combination, int start, int k, int n) {
		// TODO Auto-generated method stub
		if(n == 0 && k == 0) {
			combinations.add(new ArrayList<>(combination));
			return;
		}
		if(k == 0 || n < ((2 * start + k - 1) * k / 2)) {
			return;
		}
		for(int i = start; i <= 9; i++) {
			combination.add(i);
			backtracking(combinations, combination, i + 1, k - 1, n - i);//递归
			combination.remove(combination.size() - 1);//回溯
		}
	}
}