---

🐌个人主页： 🐌 叶落闲庭
💨我的专栏：💨
c语言
数据结构
javaEE
操作系统
Redis

石可破也，而不可夺坚；丹可磨也，而不可夺赤。

---

一、二叉树的中序遍历

1.1 题目描述

给定一个二叉树的根节点 root ，返回它的中序遍历 。

---

---

---

1.2 思路分析

返回二叉树的中序遍历，就是在遍历二叉树的时候，先访问二叉树的左子节点，然后访问二叉树的根节点，最后访问二叉树的右子节点，对于每个子节点，也是这样访问。
对于一个给定的二叉树，可以通过栈来实现它的中序遍历：

• 要求：返回一个集合，集合中的元素是二叉树中序遍历后的节点值
• 定义一个集合，用来作为返回值，当二叉树为空时，返回一个空集合
• 二叉树不为空，则定义一个栈，用来实现二叉树的中序遍历，定义一个节点指针cur，表示当前节点，当cur不为空或者栈不为空时，进入循环，在循环内再嵌套一个条件为cur不为空的循环，在嵌套的循环中将当前节点加入到栈中，并将当前节点指向当前节点的左子节点，直到将所有的左子节点均添加到栈中，内嵌循环结束，外部循环继续执行，将此时的栈顶元素弹出，并将弹出的节点值加入到集合中，将cur指向弹出的栈顶元素的右子节点，循环遍历，直到栈为空时退出循环，返回集合。

1.3 代码演示

public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        if (root == null) {
            return list;
        }
        //定义一个栈
        Stack<TreeNode> stack = new Stack<>();
        //定义当前节点指针
        TreeNode cur = root;
        while(cur != null || !stack.empty()) {
            while(cur != null) {
                stack.push(cur);
                cur = cur.left;
            }
            TreeNode top = stack.pop();
            list.add(top.val);
            cur = top.right;
        }
        return list;
    }

二、二叉树的最大深度

2.1 题目描述

给定一个二叉树 root ，返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

---

---

---

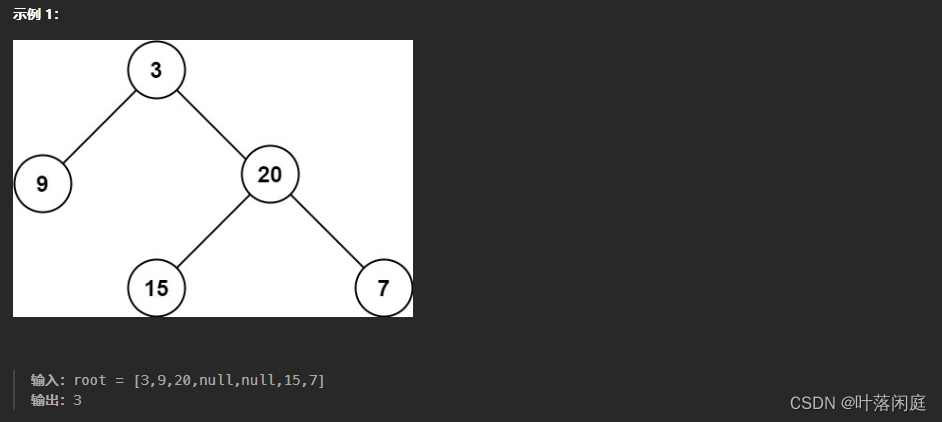
2.2 思路分析

根据题目分析，可以对二叉树进行层序遍历（最广深度优先），每遍历一层，深度数加1，当遍历到最后一层，此时的深度数就是这个二叉树的最大深度，对于二叉树的层序遍历，可以采用队列的方式实现：

• 当二叉树为空时：返回0
• 当二叉树非空，定义一个整型变量表示要返回的深度数，创建队列，并将根节点加入到队列中，当队列不为空时，开始对二叉树的每一层进行遍历，内嵌循环当队列的大小大于0时，开始内嵌循环，弹出队首元素，并记录这个节点，判断弹出的节点是否有左右子节点，若有将左右子节点加入队列，然后队列的大小自减继续内嵌循环的执行，当内嵌循环结束时，标志着第一层遍历结束，此时要将深度数自增1，开始第二层遍历，直到整个队列为空时，循环结束，返回深度数。

2.3 代码演示

public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        //定义要返回的深度数
        int result = 0;
        //创建队列
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        queue.offer(root);
        while(!queue.isEmpty()) {
            //根据队列的大小决定内层循环
            int size = queue.size();
            while(size > 0) {
                //弹出队首元素
                TreeNode top = queue.poll();
                //判断队首元素是否存在左右子元素
                if(top.left != null) {
                    //将左子元素添加到队列中
                    queue.offer(top.left);
                }
                if(top.right != null) {
                    //将右子元素添加到队列中
                    queue.offer(top.right);
                }
                //遍历结束size自减1
                size--;
            }
            //每层循环结束返回的深度数自增1
            result++;
        }
        return result;
    }

三、翻转二叉树

3.1 题目描述

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

---

---

---

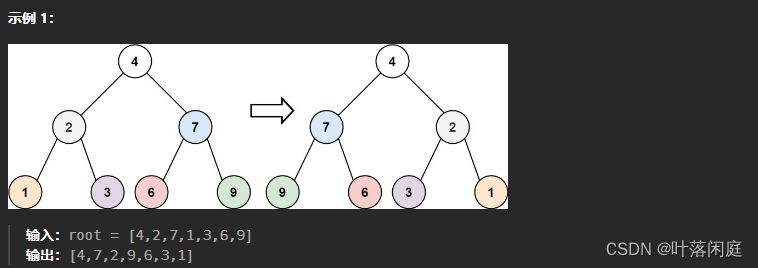
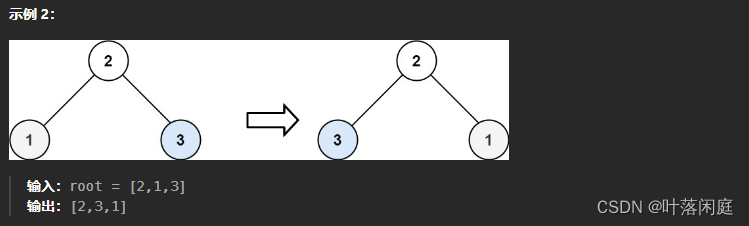
3.2 思路分析

将一棵二叉树进行翻转得到新的二叉树，可以通过队列实现，每次向队列中添加元素，弹出时交换该元素左右子节点的位置，遍历每一个节点：

• 当二叉树为空时：返回空
• 当二叉树不为空，创建一个队列，将根节点加入队中，当队列不为空时，开始外部循环，定义一个整型表示队列的大小，当队列的大小大于0时，开始内部循环，在内部循环中，先将队首元素弹出，并定义一个变量记录弹出的节点，然后判断该节点是否有左右子节点，若有则添加到队列中，然后交换弹出元素的左右子节点的位置，size自减1，若队列中无元素则开始遍历第二层，第二层队列的大小为2.大于0，则开始内部循环，同样弹出队首元素，并判断是否存在左右子节点，若存在就加入到队中，然后交换弹出的队首元素的左右子节点的位置，size自减1,之后为1，继续内部循环，仍弹出队首元素并判断是否有左右子节点，若有则添加到队列中，然后交换队首元素左右子节点的位置，size自减1，跳出内部循环，开始第三层遍历，直到外部循环判断条件的队列为空时整个循环结束，返回root根节点。

3.3 代码演示

public TreeNode invertTree(TreeNode root) {
        //非空判断
        if(root == null) {
            return null;
        }
        //创建一个队列
        Queue<TreeNode> queue = new LinkedList<>();
        //将初始根节点添加到队列中
        queue.offer(root);
        while(!queue.isEmpty()) {
            //拿到队列此时的大小，开始遍历
            int size = queue.size();
            while(size > 0) {
                //将队首元素弹出
                TreeNode top = queue.poll();
                //判断队首元素是否有左右子元素
                if(top.left != null) {
                    //将左元素入队
                    queue.offer(top.left);
                }
                if(top.right != null) {
                    //将右元素入队
                    queue.offer(top.right);
                }
                //交换队首元素左右子元素的位置
                TreeNode temp = top.left;
                top.left = top.right;
                top.right = temp;
                //size自减继续判断子元素是否有子元素
                size--;
            }
        }
        return root;
    }

四、对称二叉树

4.1 题目描述

给你一个二叉树的根节点root ， 检查它是否轴对称。

---

---

---

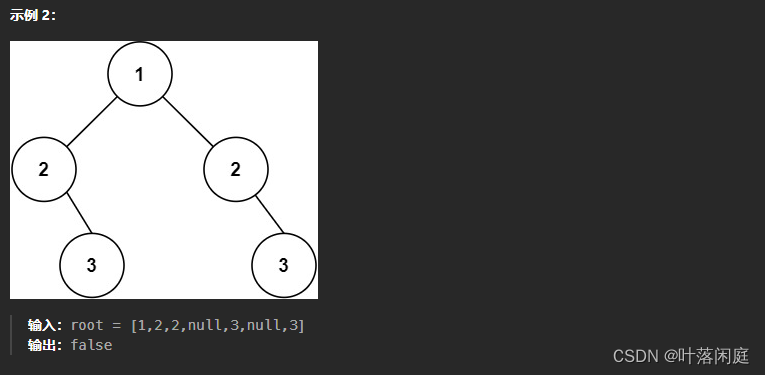
4.2 思路分析

判断二叉树的左右子节点是否关于根节点轴对称，可以通过递归判断（比较简单），也可以通过队列对这个二叉树进行遍历，每遍历一个节点就判断它的左右子节点是否相等从而判断出是否关于根节点轴对称：

• 1.递归：
• • 当根为null时，表示二叉树为空，此时应返回true
• • 当根不为null时，返回递归函数，递归函数的参数为根的左子节点和根的右子节点。递归函数中判断若两个参数均为空则返回true，若只有一个参数为空则返回false，若两个参数的值不相等，同样返回false，最后函数的返回值为回调两次递归函数并将这两个递归函数左与（即&&），两个函数的参数分别为（左左，右右）和（左右，右左）。
• 2. 队列：
• • 当根节点为空或者根的左为空同时根的右为空时，返回true
• • 创建队列，将根的左右子元素加入队列中，当队列不为空时，弹出两个元素，若两个元素均为空，则直接进行下一次循环判断，还是循环遍历从队列中弹出两个元素判断它们的值是否相等，若不相等，直接返回false，若某个节点为空，直接返回false,若两个节点都不为空，则向队列中添加左的左，右的右，左的右，右的左，再次循环判断，若能跳出循环，表示这个二叉树的左右子节点就是一根为轴的对称二叉树。

4.3 代码演示

• 递归：

public boolean isSymmetric(TreeNode root) {
     //递归思想
     if(root == null) {
         return true;
     }
     return dfs(root.left,root.right);
}   

public boolean dfs(TreeNode left,TreeNode right) {
        if(left == null && right == null) {
            return true;
        }
        if (left == null || right == null) {
            return false;
        }
        if (left.val != right.val) {
            return false;
        }
        return dfs(left.left,right.right) && dfs(left.right,right.left);
    }

• 队列：

public boolean isSymmetric(TreeNode root) {
        if(root == null || (root.left == null && root.right == null)) {
            return true;
        }
        //创建队列
        Queue<TreeNode> queue = new LinkedList<>();
        //将二叉树的左右子元素放入队列中
        queue.offer(root.left);
        queue.offer(root.right);
        while(queue.size() > 0) {
            TreeNode left = queue.poll();
            TreeNode right = queue.poll();
            if(left == null && right == null) {
                continue;
            }
            if (left == null || right == null) {
                return false;
            }
            if (left.val != right.val) {
                return false;
            }
            queue.offer(left.left);
            queue.offer(right.right);
            queue.offer(left.right);
            queue.offer(right.left);
        }
        return true;
    }