等差数列的划分

力扣链接

• 子数组 ⇒ dp[i]的含义: yinums[i] 为结尾的所有子数组中的 等差数列数组最多的个数
• 子数组⇒ 状态转移方程: 根据最后一个元素的构成
  
  
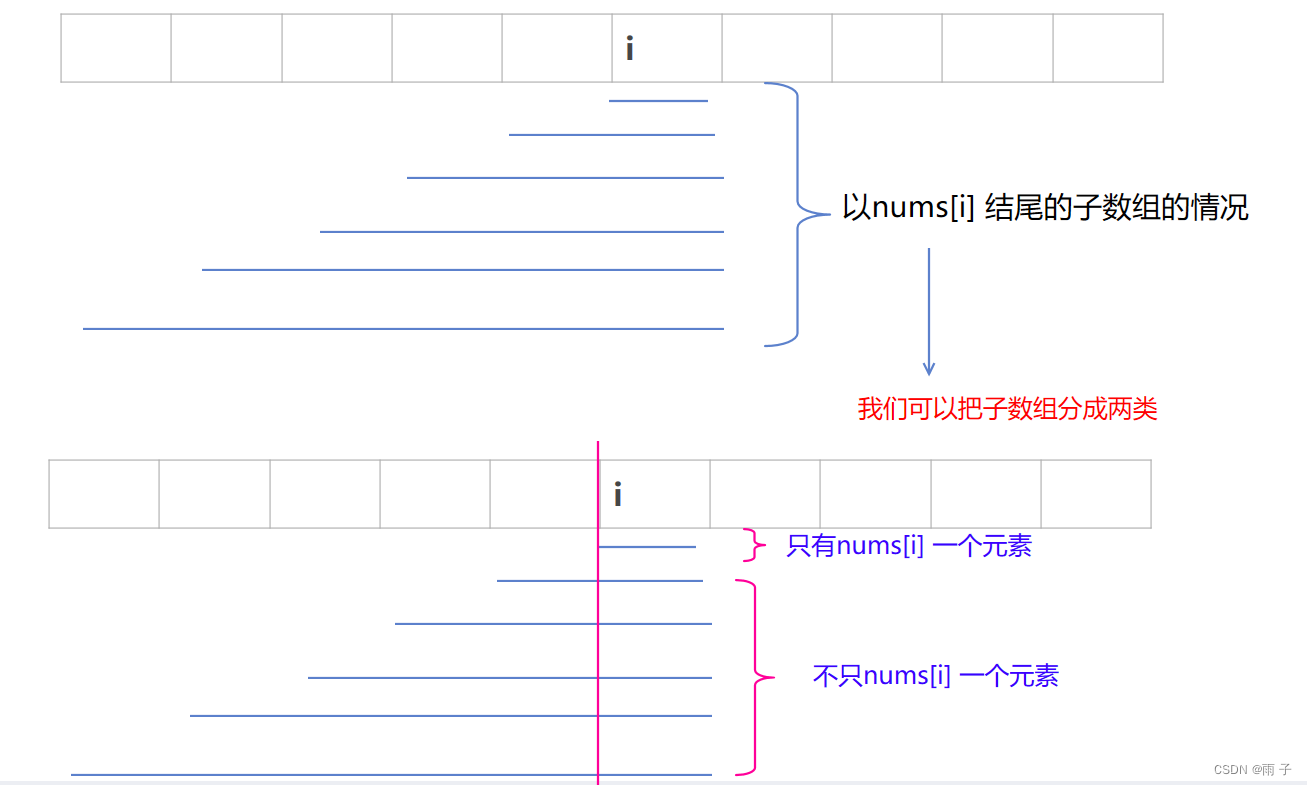
• 初始化: 涉及到 i-1, i-2 ⇒ 所以要初始化dp[0] 和 dp[1]
  都初始化为 0 ⇒ 1. 等差数列数组要三个元素及以上, dp[0] = dp[1] = 0; 2. 少考虑两种状态
• 遍历方向: 从前往后
• 返回结果: 返回数组 nums 中所有为等差数组的 子数组 个数 ⇒ 累加dp表

class Solution {
public:
    int numberOfArithmeticSlices(vector<int>& nums) 
    {
        int n = nums.size();

        // 建表 + 初始化
        vector<int> dp(n);

        int res = 0;
        for(int i = 2; i < n; i++)
        {
            if(nums[i-1] * 2 == nums[i] + nums[i-2])
                dp[i] = dp[i-1] + 1;

            res += dp[i];
        }

        return res;
    }
};

---

最长递增子序列

力扣链接

• 子序列 ⇒ dp[i]的含义: 以nums[i] 为结尾的 所有子序列中 最长递增子序列的长度
• 子序列 ⇒ 状态转移方程: 根据最后一个元素的构成
  
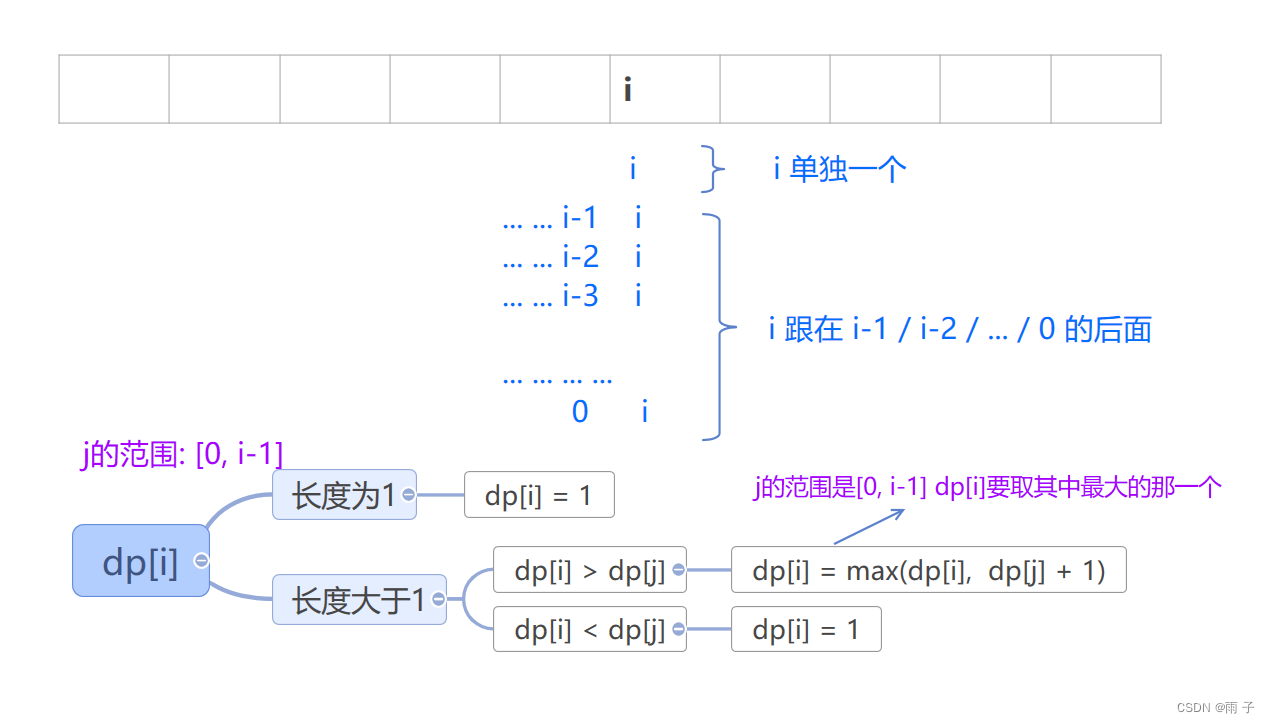
• 初始化: 全都初始化为 1
• 遍历方向: 从前往后
• 返回结果: dp表中的最大值

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) 
    {
        int n = nums.size();

        // 建表 + 初始化
        vector<int> dp(n, 1);

        int res = 1;
        for(int i = 1; i < n; i++)
        {
            for(int j = 0; j < i; j++)
            {
                if(nums[i] > nums[j])
                    dp[i] = max(dp[i], dp[j] + 1);
            }

            res = max(res, dp[i]);
        }

        return res;
    }

};

---

仰望星空, 脚踏实地!