题目描述
给出一张 n 行 m 列仅由黑白方格组成的黑白图片(行从上到下 1 到 n 编号,列从左到右 1 到 m 编号)。如下图是一张由 17 行 18 列方格构成的黑白图片,图片中的任意一个方格要么是白色,要么是黑色。
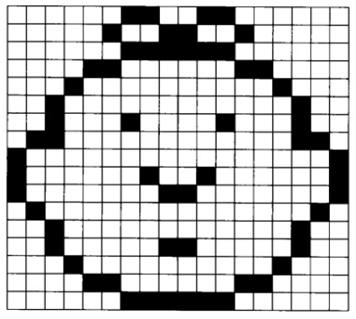
仔细观察这张黑白图片我们可以发现,图中共有 60 个黑色方格(连续的黑色方格不能算成一个),黑色方格最多的行是第 3 行和第 17 行,都为 6 个,黑色方格最少的行是第 5行、第 6 行、第 9 行、第 12 行、第 13 行、第 15 行,都为 2 个。
请编写程序统计黑白图片中黑色方格的总数,黑色方格数目最多的行的行号及黑色方格数目最少的行的行号。
输入
输入共 n+1 行。
第 1 行是两个整数 n 和 m(1≤n, m≤100),分别表示黑白图片的行数和列数,两个整数间用空格分隔。
第 2 行到第 n+1 行,描述了图片中每个方格的颜色,黑色用整数 0 表示,白色用整数 1表示。每行为 m 个用空格分隔的 0 或 1,其中第 i+1 行第 j 列的整数为 Aij(1≤i≤n,1≤j≤m,Aij=0 或者 Aij=1),表示图片第 i 行第 j 列位置的方格颜色。
输出
输出共 1 行,包含 3 个整数。分别表示输入文件所表示的黑白图片中黑色方格的总数,黑色方格数目最多的行的行号及黑色方格数目最少的行的行号。注意,如果黑色方格最多的行有多行一样,则输出行号最小的,同样,如果黑色方格最少的行有多行一样,也是输出行号最小的。
样例输入
6 6
1 1 1 1 1 1
1 0 1 0 0 1
1 0 1 1 0 1
1 0 1 0 1 1
1 0 1 0 0 1
1 1 1 1 1 1样例输出
10 2 1提示
【样例解释】
输入的黑白图片的大小为 6 行 6 列,第 1 行 0 个黑色方格,第 2 行 3 个黑色方格,第 3 行 2 个黑色方格,第 4 行 2 个黑色方格,第 5 行 3 个黑色方格,第 6 行 0 个黑色方格。所以 总共有 10 个黑色方格,黑色方格最多且行号最小的行是第 2 行,黑色方格最少且行号最小 的行是第 1 行。
【数据范围约定】
所有的输入数据保证 1≤n, m≤100。
来源
慈溪竞赛-2013
C++:
#include<bits/stdc++.h>
using namespace std;
int main(){
int a,b,hei=0,hmax=1,hmin=1,hang[1005]={};
cin>>a>>b;
char c[1005][1005];
for(int i=1;i<=a;i++){
for(int j=1;j<=b;j++){
cin>>c[i][j];
if(c[i][j]=='0'){
hei++;
hang[i]++;
}
}
if(hang[i]>hang[hmax]){
hmax=i;
}
if(hang[i]<hang[hmin]){
hmin=i;
}
}
cout<<hei<<" "<<hmax<<" "<<hmin;
return 0;
}