目录

题目：

示例：

分析：

代码：

---

题目：

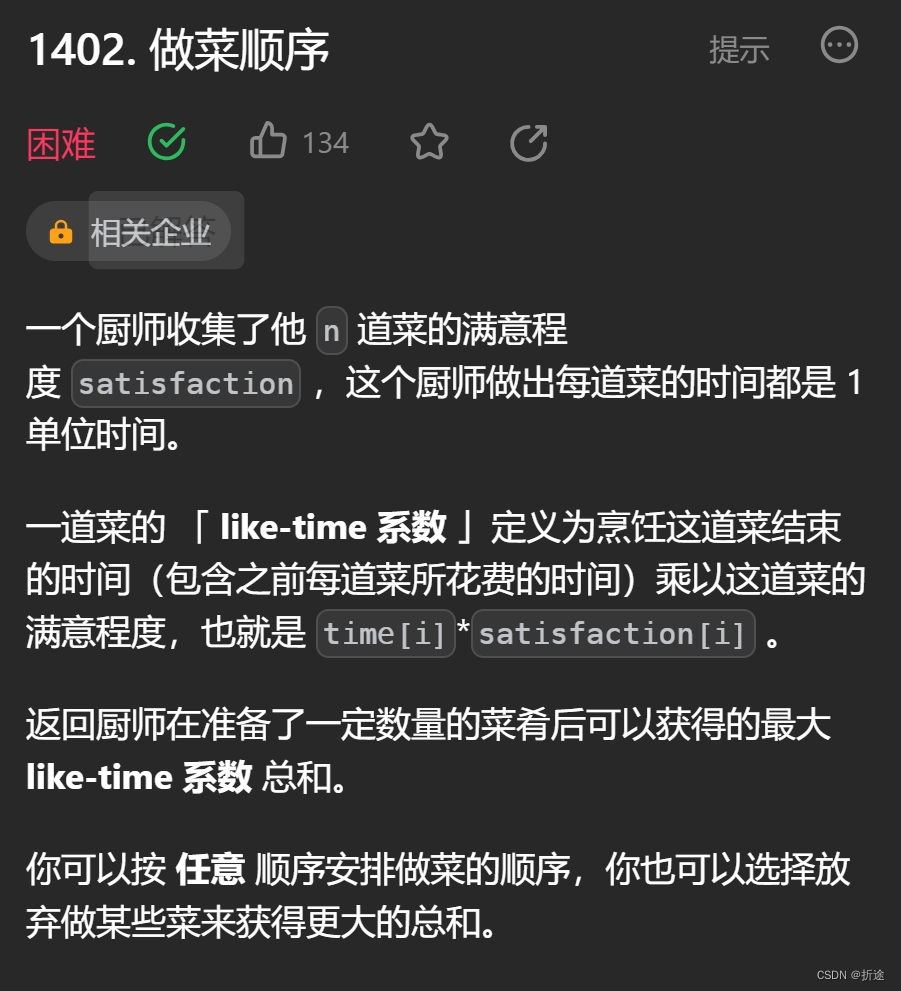
示例：

分析：

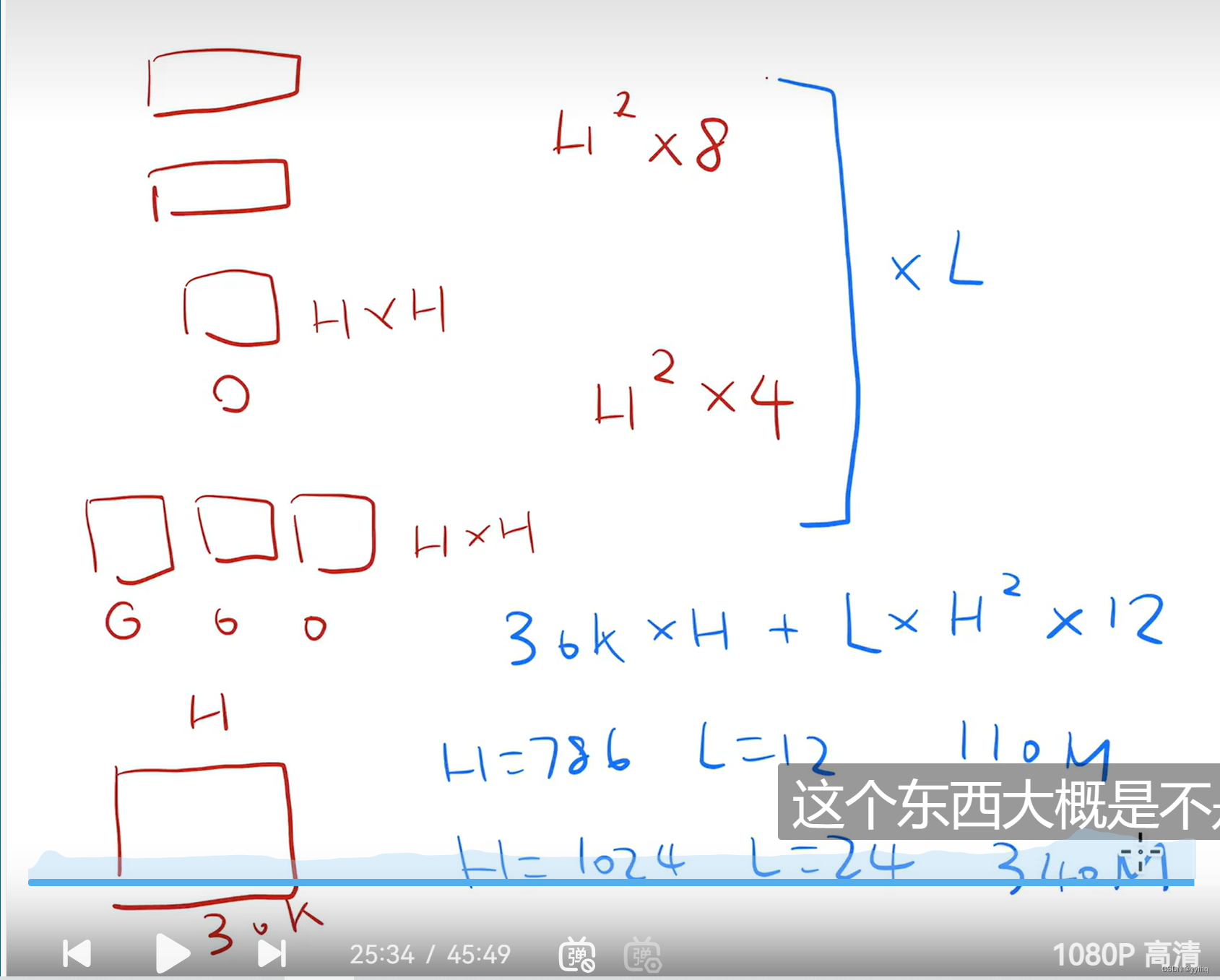
给我们一个数组表示每个菜的满意度，我们可以指定做哪些菜以及做的顺序，需要我们凑到一个系数的最大值，系数的公式为 菜的满意度 * 轮到做完这盘菜所耗的时间包括等待时间。

我们可以知道，决定这个系数大小的有两个因素，第一个是满意度，另一个其实是做菜的顺序，越是后面做的菜，第二个因素就越大，系数也就越大。

所以我们定下主基调了，满意度越大的菜我们就放到越后面去做，因此我们可以先对满意度进行排序。做菜的顺序我们就定下来了，剩下的问题就是选择做哪些菜。

比较直观的选择就是我们只选择满意度为正数的菜，因为如果选择了负数，那么会导致总体的满意度减少。

但是事实是有时候我们选择满意度为负数的菜反而会让总体的满意度上升，因为如果我们先做了负数的菜，后面再做满意度高的菜，则会使得等待时间变久，这样子满意度系数也会更大。

如果满意度为正，我们就必须选择要做这盘菜，重点在于我们应该如何挑选满意度为负数的菜。

一盘菜能贡献的满意度系数为满意度乘上等待时间，那么是不是就说明在一盘菜之前每多做一盘菜，那么这盘菜的满意度系数就会多加上这盘菜的满意度，转换成数学式子就是  i * ( j + 1 ) = i * j + i 。

我们逆向思考一下，我们一开始说满意度越高的菜我们越后面做，这个是没问题的，但是不利于我们做这道题，我们可以先假设我做满意度最高的菜，如果后面的菜我需要做了，我再反悔一下，我改成后面的菜变成第一个做的菜，而一开始先做的满意度最高的菜我改成第二个做的，这时我只需要将系数总和再加上满意度最高的菜的满意度就可以完成反悔的操作。

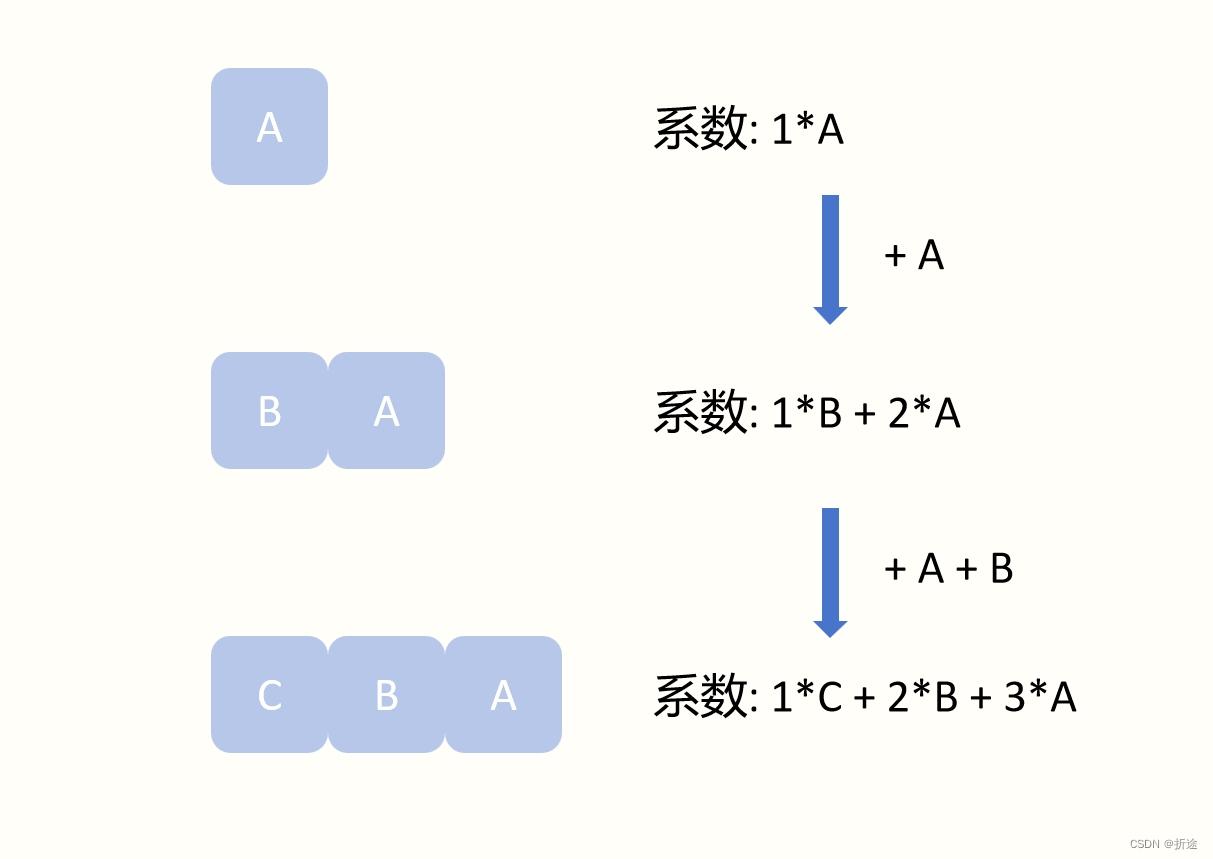
 也就是说，我之后每做一盘菜，那么我们的系数之和就会加上之前已经做过的菜的满意度之和了，这也就是前缀和。

因此如果遇到了满意度为负数的菜，只要这个菜的满意度加上前缀和大于0了，那么总的满意度系数还是会增加的，我们就可以去做这盘菜。

这样做菜的顺序和做菜的选择我们都搞定了，这道题也就迎刃而解了。

代码：

class Solution {
public:
    int maxSatisfaction(vector<int>& satisfaction) {
        int res=0;
        //前缀和
        int cache=0;
        int n=satisfaction.size();
        //从大到小排序
        sort(satisfaction.begin(),satisfaction.end(),[](auto &a,auto &b){return a>b;});
        for(int i=0;i<n;++i){
            //如果是正数,则肯定是正收益,那么直接加上
            //如果是负数,如果扣掉前缀和之后仍有盈余,那么也加上
            if(satisfaction[i]>=0||-1*satisfaction[i]<cache){
                cache+=satisfaction[i];
                res+=cache;
            }
        }
        return res;
    }
};