系列前文:【经典 PageRank 】01/2 PageRank的基本原理-CSDN博客
一、说明
并非所有连接都同样重要!
该算法由 Sergey 和 Lawrence 开发,用于在 Google 搜索中对网页进行排名。基本原则是重要或值得信赖的网页更有可能链接到其他重要网页。例如,来自信誉良好的网站的链接比来自不太知名的博客的链接具有更大的权重。
特征向量在理解 PageRank 算法的理论中发挥着基础作用。PageRank 和特征向量之间的联系可以在马尔可夫链或计算图及其稳态行为的背景下得到最好的理解。
二、特征向量和特征值
对于给定的方阵A和非零向量v,如果向量v满足方程A*v = λ*v ,则它是A的特征向量。这里,λ是称为特征值的标量,对应于特征向量v。从概念上讲,特征向量和特征向量是成对的值,其中特征向量在向量空间的某个基上具有向量变换的方向,特征值描述变换的大小。
2.1 网页排名
让我们将网络视为马尔可夫链,其中网页是节点或状态,页面之间的超链接作为方向边表示从一个页面转到另一页面的概率。当我们将此马尔可夫链表示为矩阵(称为转移矩阵)时,PageRank 算法的目标是找到一个稳态向量,其中概率总和为 1 或者没有进一步变化或收敛。查找页面排名的表达式由下式给出:
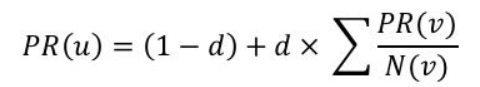
其中u:当前网页,d:阻尼因子,PR( v) :页面v的页面排名,N(v) :从v发出的链接数量
在 PageRank 的背景下,主导特征向量(对应于最大特征值的特征向量,在随机矩阵的情况下为 1)代表马尔可夫链的稳态分布。这种稳态分布就是我们试图计算的 PageRank 分数:系统中所有网页的概率分布,其中出现在页面上的概率不再随着进一步的转换而变化。
幂迭代方法涉及将向量(初始 PageRank 分数)重复乘以转移矩阵,本质上近似于该主特征向量。随着时间的推移,这个过程将会收敛,得到的向量将与矩阵的主特征向量成正比,从而给出网页的 PageRank 分数。
收敛背后的原因是,随着每次相乘(或转变),主要特征值的影响会增加,而其他特征值的影响会减小,特别是当引入阻尼因子时。最终,这导致向量与主特征向量成比例。
2.2 执行算法
- 将所有条目的页面排名得分矩阵初始化为 PR = 1/N。
- 表示网页- 如前所述,网络被想象为有向计算图。
- 阻尼因子- 引入来模拟随机网络冲浪者的行为,因为冲浪者大部分时间都会以概率d跟踪链接,但也会以(1-d)的概率移动到随机页面。
- 迭代- 使用上述表达式计算页面排名,直到它们收敛。
- 标准化- 经过几次迭代后,PageRank 值被标准化为总和为 1,以检查最大特征值 1。
def PageRank(transition_matrix, d, max_iterations, conv_thres):
'''
Arguments:
transition_matrix: a matrix or numpy array representing the probabilities of going from one page to another
d: damping factor
max_iterations: number of iterations
conv_thres: convergence threshold
Return: ranks of each webpage, as columns of the transition matrix
'''
#total number of web pages
N = transition_matrix.shape[0]
#Intializing the transition matrix with equal probabilities
PR = np.ones(N)/N
for _ in range(max_iterations):
PR_new = (1-d)/N + d*np.matmul(transition_matrix,PR)
#normalizing the rank scores
PR_norm = np.linalg.norm(PR_new - PR, 1)
#covergence constraint
if PR_norm <= conv_thres:
return PR_new
PR = PR_new
return PR 现在,让我们编写一个脚本,将转换矩阵可视化为马尔可夫链,其中网页作为状态或节点,超链接作为从一个页面移动到另一页面的概率。
def markov_chain(transition_matrix):
# Create a directed graph.
G = nx.DiGraph()
# Nodes represent pages. Assume node labels are 0, 1, 2, ... for simplicity.
num_nodes = transition_matrix.shape[0]
G.add_nodes_from(range(num_nodes))
# Iterate through the transition matrix to create edges.
for i in range(num_nodes):
for j in range(num_nodes):
if transition_matrix[i, j] > 0: # Add edge if there's a non-zero transition probability.
G.add_edge(i, j, weight=transition_matrix[i, j])
# Visualize the graph.
pos = nx.spring_layout(G)
nx.draw_networkx_nodes(G, pos)
nx.draw_networkx_labels(G, pos)
nx.draw_networkx_edge_labels(G, pos, edge_labels={(u, v): f"{d['weight']:.2f}" for u, v, d in G.edges(data=True)})
nx.draw_networkx_edges(G, pos)
plt.title("Markov Chain from Transition Matrix")
plt.axis("off")
plt.show()三、实验代码
这是 GitHub 存储库链接:ashu1069/PageRank (github.com),由 python 脚本和 Jupyter Notebook 组成。该脚本包含使用自定义输入的驱动程序代码,其余部分在自述文件中进行了解释。
本质上,PageRank 值代表从网络链接结构导出的转换矩阵的主要特征向量。特征向量和特征值的数学为我们提供了计算这些值的理论基础和实用方法(幂迭代)。
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
def PageRank(transition_matrix, d, max_iterations, conv_thres):
'''
Arguments:
transition_matrix: a matrix or numpy array representing the probabilities of going from one page to another
d: damping factor
max_iterations: number of iterations
conv_thres: convergence threshold
Return: ranks of each webpage, as columns of the transition matrix
'''
#total number of web pages
N = transition_matrix.shape[0]
#Intializing the transition matrix with equal probabilities
PR = np.ones(N)/N
for _ in range(max_iterations):
PR_new = (1-d)/N + d*np.matmul(transition_matrix,PR)
#normalizing the rank scores
PR_norm = np.linalg.norm(PR_new - PR, 1)
#covergence constraint
if PR_norm <= conv_thres:
return PR_new
PR = PR_new
return PR
def markov_chain(transition_matrix):
# Create a directed graph.
G = nx.DiGraph()
# Nodes represent pages. Assume node labels are 0, 1, 2, ... for simplicity.
num_nodes = transition_matrix.shape[0]
G.add_nodes_from(range(num_nodes))
# Iterate through the transition matrix to create edges.
for i in range(num_nodes):
for j in range(num_nodes):
if transition_matrix[i, j] > 0: # Add edge if there's a non-zero transition probability.
G.add_edge(i, j, weight=transition_matrix[i, j])
# Visualize the graph.
pos = nx.spring_layout(G)
nx.draw_networkx_nodes(G, pos)
nx.draw_networkx_labels(G, pos)
nx.draw_networkx_edge_labels(G, pos, edge_labels={(u, v): f"{d['weight']:.2f}" for u, v, d in G.edges(data=True)})
nx.draw_networkx_edges(G, pos)
plt.title("Markov Chain from Transition Matrix")
plt.axis("off")
plt.show()
if __name__ == '__main__':
transition_matrix = np.array([
[0.1,0.5,0.4],
[0.2,0,0.2],
[0,0.3,0.3]
])
d = 0.85
max_iterations = 1000
conv_thres = 1e-6
PR = PageRank(transition_matrix, d, max_iterations, conv_thres)
print(f'PageRanks:{PR}')
markov_chain(transition_matrix)参考资料:
搜索引擎的剖析 (stanford.edu)
阿舒托什·库马尔