1 )回顾 WebGL 三种面的适应场景
- TRIANGLES 单独三角形
- TRIANGLE_STRIP 三角带
- TRIANGLE_FAN 三角扇
- 备注
- 在实际的引擎开发中,TRIANGLES 是用得最多的
- TRIANGLES 的优势是可以绘制任意模型,缺点是比较费点
2 )适合 TRIANGLES 单独三角形的的模型

- 比如上述这个不规则图形
3 )TRIANGLE_STRIP 和TRIANGLE_FAN 的优点和缺点
- TRIANGLE_STRIP 和TRIANGLE_FAN 的优点是相邻的三角形可以共用一条边,比较省点
- 然而其缺点也太明显,因为它们只适合绘制具备相应特点的模型
- 适合TRIANGLE_STRIP三角带的模型如下

- 适合TRIANGLE_FAN三角扇的模型如下

- 扩展:
- three.js 使用的绘制面的方式就是TRIANGLES,可以在其 WebGLRenderer 对象的源码的 renderBufferImmediate 方法中查看
_gl.drawArrays(_gl.TRIANGLES, 0, object.count);
- three.js 使用的绘制面的方式就是TRIANGLES,可以在其 WebGLRenderer 对象的源码的 renderBufferImmediate 方法中查看
4 )图形转面的基本步骤
- 在three.js 里有一个图形几何体ShapeGeometry,可以把图形变成面。

- 只要有数学支撑,就可以实现这种效果
5 )使用TRIANGLES 独立三角形的方式,将图形转成面
-
原理
- 使用的方法叫做“砍角”
- 其原理就是从起点将多边形中符合特定条件的角逐个砍掉,然后保存到一个集合里
- 直到把多边形砍得只剩下一个三角形为止。
- 这时候集合里的所有三角形就是我们想要的独立三角形。
-
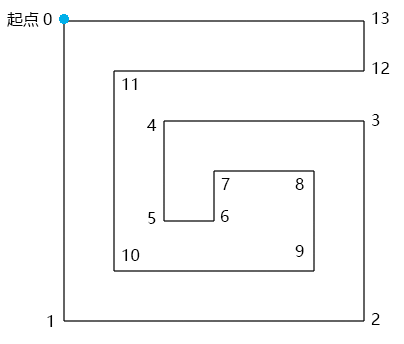
举个例子
-
已知:逆时针绘图的路径G
-
求:将其变成下方网格的方法
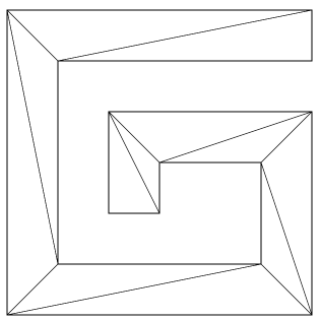
- 求解步骤
- 1)寻找满足以下条件的 ▲ABC
- ▲ABC 的顶点索引位置连续,如:012、123、234
- 比如,012时,A是0,B是1,C是2
- 点C在向量AB的正开半平面里,可以理解为你站在A点,面朝B点,点C要在你的左手边
- ▲ABC 中没有包含 路径G 中的其它顶点
- 2)当找到 ▲ABC 后,就将点B从路径的顶点集合中删掉,并将ABC三个点存入集合中,然后继续往后找。
- 3)当路径的定点集合只剩下3个点时,就结束。
- 4)由所有满足条件的 ▲ABC 构成的集合就是我们要求的独立三角形集合。
- 1)寻找满足以下条件的 ▲ABC
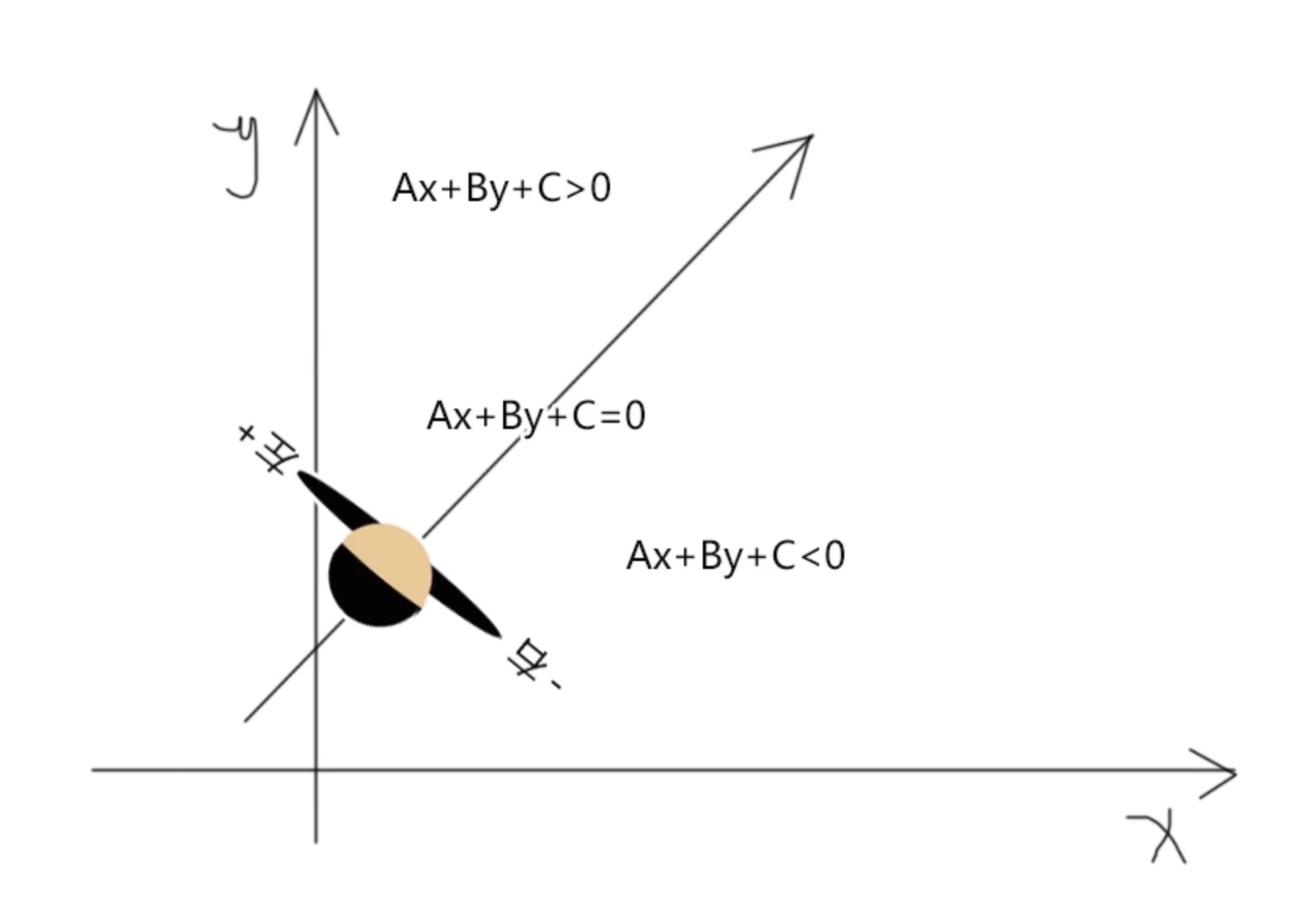
- 在上述坐标系示例中,可辅助我们找到C点
- A是起点,B是第二个点,C则是第三个点,用这个方法,可以看到C点是否在向量AB(A->B)的左手边
- 砍角的精髓就在于不断消耗B,让图形可砍,逐渐砍完,比如B点是5时满足条件,5被干掉,下一轮砍角就可组 4,6,7 这个三角形
- 每一轮都是按照顺序(不一定是升序,因为可能从最后一个点x,0,1这样组)找三个点组成一个三角形,判断这个三角形是否符合被砍的标准
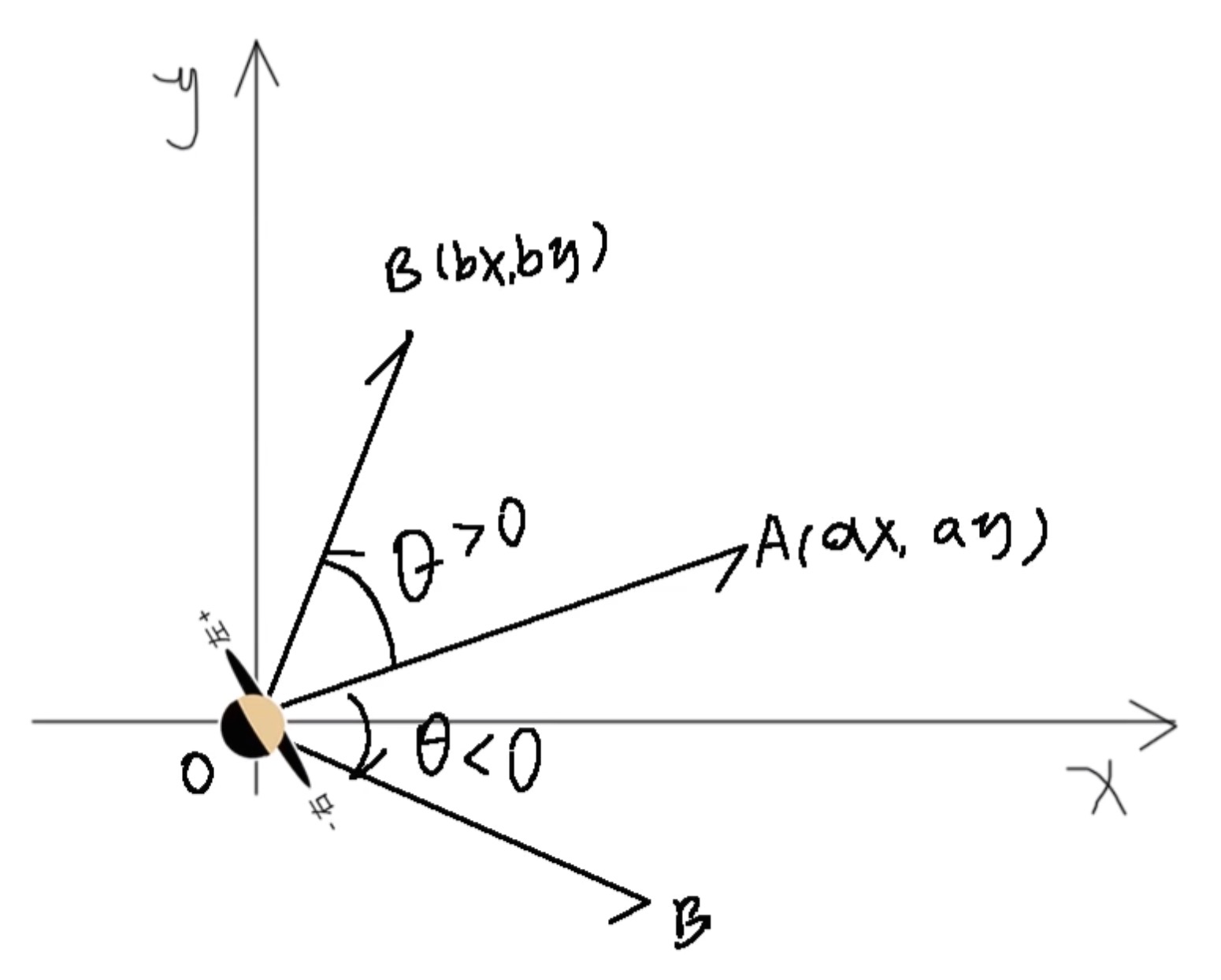
- 上面这个图形, 进一步理解如何判断一个点,比如B,在一个向量OA的左侧还是右侧
- 从 OA 转到 OB 需要 θ \theta θ 度,如果 这个角度大于零,则B在OA的左侧,反之,则在右侧
- 如何判断 这个
θ
\theta
θ 是 大于零 还是 小于零, 有一个算法可以使用:
- s i n θ ∗ ∣ O A ∣ ∗ ∣ O B ∣ = a x ∗ b y − a y ∗ b x sin \theta * |OA| * |OB| = ax * by - ay * bx sinθ∗∣OA∣∗∣OB∣=ax∗by−ay∗bx
- 在这个公式中,|OA|, |OB| 都是绝对值,都是 >=0 的,所以,只要后面的 a x ∗ b y − a y ∗ b x > 0 ax * by - ay * bx > 0 ax∗by−ay∗bx>0, 则 s i n θ > 0 sin \theta > 0 sinθ>0, θ > 0 \theta > 0 θ>0
- 这样就可判断出一个点在向量的哪一侧了
图形转面的实现
1 )绘制路径G
- 路径G的顶点数据
const pathData = [ 0, 0, 600, 0, 600, 100, 100, 100, 100, 500, 500, 500, 500, 300, 300, 300, 300, 400, 200, 400, 200, 200, 600, 200, 600, 600, 0, 600 ];- 这一些数据是CSS的顶点数据,走的是CSS的坐标系
- 画CSS的时候,需要逆时针绘图
- 在CSS坐标系,水平的是 x轴(向右为正),垂直的是 y轴(向下为正), 原点在左上角

- 在上图中,就是数据对应的图形,原点 (0, 0) 对应左上角,逆时针绘制出来的
- 在pathData里两个数字为一组,分别代表顶点的x位和y位
- pathData里的数据是我以像素为单位画出来的,在实际项目协作中,UI给我们的svg文件可能也是以像素为单位画出来的,这个我们要做好心理准备
- 因为,webgl画布的宽和高永远都是两个单位
- 所以,我们要将上面的点画到webgl 画布中,就需要做一个数据映射
2 )在webgl 中绘制正方形
-
从pathData 数据中我们可以看出,路径G的宽高都是600,是一个正方形。
-
所以,我可以将路径G映射到webgl 画布的一个正方形中。
-
这个正方形的高度我可以暂且定为1,那么其宽度就应该是高度除以canvas画布的宽高比。
//宽高比 const ratio = canvas.width / canvas.height; // 正方形高度 这里 1 实际上是整个canvas画布高度的一半 const rectH = 1.0; // 正方形宽度 (这里是由宽高比计算出来的) 在webgl坐标系上宽度上一个单位和高度上一个单位可能是不一样的,是根据canvas画布来走的 const rectW = rectH / ratio;
3 )正方形的定位,把正方形放在webgl画布的中心
-
获取正方形尺寸的一半,然后求出其x、y方向的两个极值即可。
//正方形宽高的一半 const [halfRectW, halfRectH] = [rectW / 2, rectH / 2]; //两个极点 const minX = -halfRectW; const minY = -halfRectH; const maxX = halfRectW; const maxY = halfRectH;
4 )利用之前的Poly对象绘制正方形,测试一下效果
// 这个 Poly 对象的实现参考前面webgl博文
const rect = new Poly({
gl,
vertices: [
minX, maxY,
minX, minY,
maxX, minY,
maxX, maxY,
],
});
rect.draw();

- 先画了4个点,效果没问题之后,就可以把数据在这个正方形里做映射了
5 )建立x轴和y轴比例尺
const scaleX = ScaleLinear(0, minX, 600, maxX);
const scaleY = ScaleLinear(0, minY, 600, maxY);
function ScaleLinear(ax, ay, bx, by) {
const delta = {
x: bx - ax,
y: by - ay,
};
const k = delta.y / delta.x;
const b = ay - ax * k;
return function (x) {
return k * x + b;
};
}
- ScaleLinear 这个方法的实现参考下文中的全部代码,是对点斜式做了一个封装,内部参数是两种坐标数据的极小值和极大值
ScaleLinear( 0, minX, 600, maxX );- 参数第一列是 css 数据; 第二列是 webgl 数据
- 参数第一行是 两种坐标数据的极小值; 第二行是 两种坐标数据的极大值
- ScaleLinear(ax, ay, bx, by) 方法使用的就是点斜式,用于将x轴和y轴上的数据像素数据映射成 webgl数据
- ax 像素数据的极小值
- ay webgl数据的极小值
- bx 像素数据的极大值
- by webgl数据的极大值
6 )将路径G中的像素数据解析为 webgl 数据
const glData = [];
for (let i = 0; i < pathData.length; i += 2) {
// 把每个点做一个解析,并存入集合中
glData.push(scaleX(pathData[i]), scaleY(pathData[i + 1]));
}
const path = new Poly({
gl,
vertices: glData,
types: ["POINTS", "LINE_LOOP"],
});
path.draw();
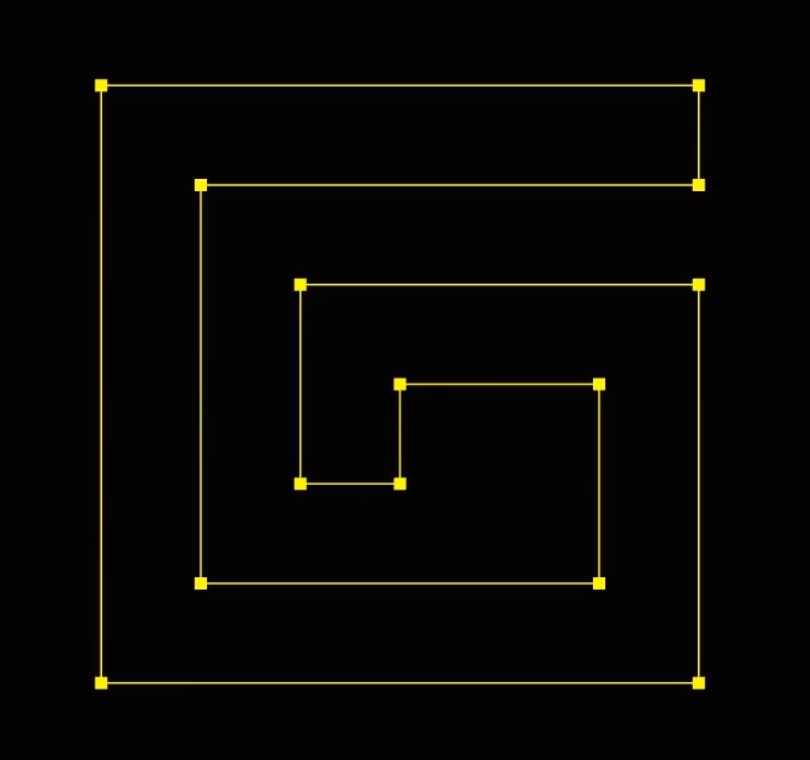
7 )将图形网格化,把图形变成面

-
建立了一个ShapeGeo 对象,用于将图形网格化
const shapeGeo = new ShapeGeo(glData) -
ShapeGeo.js
export default class ShapeGeo { constructor(pathData = []) { this.pathData = pathData; // 路径数据 平铺展开 this.geoData = []; // 将路径数据 转换成 对象型数组 方便操作 this.triangles = []; // 存储的三角形集合 this.vertices = []; // 平铺展开的 独立三角形数据,后面会交给缓冲区进行渲染 this.parsePath(); // 将 pathData 转换成 geoData this.update(); // 更新方法,默认执行 } update() { this.vertices = []; this.triangles = []; this.findTriangle(0); // 寻找独立三角形 this.upadateVertices() // 从独立三角形区域解析出 vertices } parsePath() { this.geoData = []; const { pathData, geoData } = this for (let i = 0; i < pathData.length; i += 2) { geoData.push({ x: pathData[i], y: pathData[i + 1] }) } } findTriangle(i) { const { geoData, triangles } = this; const len = geoData.length; if (geoData.length <= 3) { triangles.push([...geoData]); } else { // 对位置做了一个加工,因为如果从最后一个点开始找,最后一个点的下一个肯定是第一个,这里对顶点长度进行取余操作,循环进行 const [i0, i1, i2] = [ i % len, (i + 1) % len, (i + 2) % len ]; const triangle = [ geoData[i0], geoData[i1], geoData[i2], ]; // 判断找的三角形是否符合条件:在左手边 && 在三角形中是否有点 if (this.cross(triangle) > 0 && !this.includePoint(triangle)) { triangles.push(triangle); // 存储三角形 geoData.splice(i1, 1); // 移除 B点 (第二个点) } this.findTriangle(i1); // 接着再从第二个点开始寻找, 这里即便第二个点被删了,之前的i2也会是这里的i1 } } includePoint(triangle) { // 遍历所有顶点 for (let ele of this.geoData) { // 判断当前三角形是否包含当前点,如果否 if (!triangle.includes(ele)) { // 判断其他点是否在这个三角形之中 if (this.inTriangle(ele, triangle)) { return true; } } } return false; } inTriangle(p0, triangle) { let inPoly = true; // 遍历三角形点 for (let i = 0; i < 3; i++) { const j = (i + 1) % 3; // j 是下一个点,这里 余3运算 和上面一样的原理 const [p1, p2] = [triangle[i], triangle[j]]; // p0 点是否在三角形每一条边的 右侧 或 左侧 if (this.cross([p0, p1, p2]) < 0) { inPoly = false; break } } return inPoly; } // 这个就是这面讲到的 θ > 0的原理中,只要右边 > 0了,θ 就 > 0 cross([p0, p1, p2]) { const [ax, ay, bx, by] = [ p1.x - p0.x, p1.y - p0.y, p2.x - p0.x, p2.y - p0.y, ]; return ax * by - bx * ay; } upadateVertices() { const arr = [] this.triangles.forEach(triangle => { for (let { x, y } of triangle) { arr.push(x, y) } }) this.vertices = arr } } -
属性
- pathData 平展开的路径数据
- geoData 由路径数据pathData 转成的对象型数组
- triangles 三角形集合,对象型数组
- vertices 平展开的对立三角形顶点集合
-
方法
- update() 更新方法,基于pathData 生成vertices
- parsePath() 基于路径数据pathData 转成对象型数组
- findTriangle(i) 寻找符合条件的三角形
- i 顶点在geoData 中的索引位置,表示从哪里开始寻找三角形
- includePoint(triangle) 判断三角形中是否有其它顶点
- inTriangle(p0, triangle) 判断一个顶点是否在三角形中
- cross([p0, p1, p2]) 以p0为基点,对二维向量p0p1、p0p2做叉乘运算
- upadateVertices() 基于对象数组geoData 生成平展开的 vertices 数据
-
绘制G形面
const face = new Poly({ gl, vertices: shapeGeo.vertices, types: ["TRIANGLES"], }); face.draw();
核心代码
<canvas id="canvas"></canvas>
<!-- 顶点着色器 -->
<script id="vertexShader" type="x-shader/x-vertex">
attribute vec4 a_Position;
void main() {
gl_Position = a_Position;
gl_PointSize = 10.0;
}
</script>
<!-- 片元着色器 -->
<script id="fragmentShader" type="x-shader/x-fragment">
void main(){
gl_FragColor = vec4(1,1,0,1);
}
</script>
<script type="module">
import { initShaders, ScaleLinear } from "./utils/utils.js";
import Poly from "../utils/Poly.js";
import ShapeGeo from "../utils/ShapeGeo.js";
const canvas = document.querySelector("#canvas");
canvas.width = window.innerWidth;
canvas.height = window.innerHeight;
// 获取着色器文本
const vsSource = document.querySelector("#vertexShader").innerText;
const fsSource = document.querySelector("#fragmentShader").innerText;
//三维画笔
const gl = canvas.getContext("webgl");
//初始化着色器
initShaders(gl, vsSource, fsSource);
//声明颜色 rgba
gl.clearColor(0, 0, 0, 1);
//刷底色
gl.clear(gl.COLOR_BUFFER_BIT);
//路径G-逆时针
const pathData = [
0, 0,
0, 600,
600, 600,
600, 200,
200, 200,
200, 400,
300, 400,
300, 300,
500, 300,
500, 500,
100, 500,
100, 100,
600, 100,
600, 0,
];
//宽高比
const ratio = canvas.width / canvas.height;
//正方形高度
const rectH = 1.0;
//正方形宽度
const rectW = rectH / ratio;
//正方形宽高的一半
const [halfRectW, halfRectH] = [rectW / 2, rectH / 2];
//两个极点
const minX = -halfRectW;
const minY = -halfRectH;
const maxX = halfRectW;
const maxY = halfRectH;
//正方形
const rect = new Poly({
gl,
vertices: [
minX, maxY,
minX, minY,
maxX, minY,
maxX, maxY,
],
});
rect.draw();
//建立比例尺
const scaleX = ScaleLinear(
0, minX,
600, maxX
);
const scaleY = ScaleLinear(
0, maxY,
600, minY
);
//将路径G中的像素数据解析为webgl数据
const glData = [];
for (let i = 0; i < pathData.length; i += 2) {
glData.push(scaleX(pathData[i]), scaleY(pathData[i + 1]));
}
const path = new Poly({
gl,
vertices: glData,
types: ["POINTS", "LINE_LOOP"],
});
path.draw();
const shapeGeo = new ShapeGeo(glData)
const face = new Poly({
gl,
vertices: shapeGeo.vertices,
types: ["TRIANGLES"],
});
face.draw();
</script>