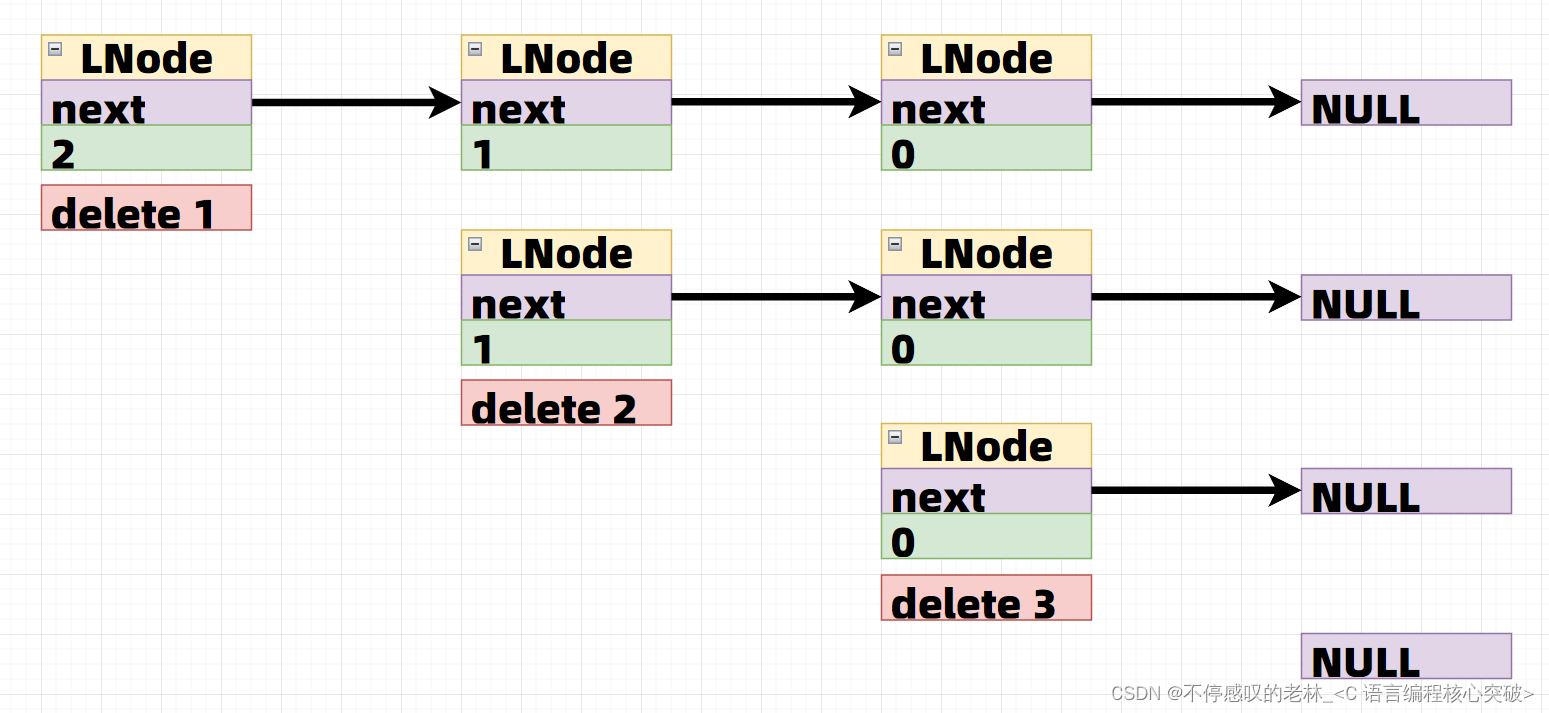
将一个 二叉搜索树 就地转化为一个 已排序的双向循环链表
对于双向循环列表，你可以将左右孩子指针作为双向循环链表的前驱和后继指针，第一个节点的前驱是最后一个节点，最后一个节点的后继是第一个节点
特别地，我们希望可以 就地 完成转换操作。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继。还需要返回链表中最小元素的指针
示例 1：
输入：root = [4,2,5,1,3]

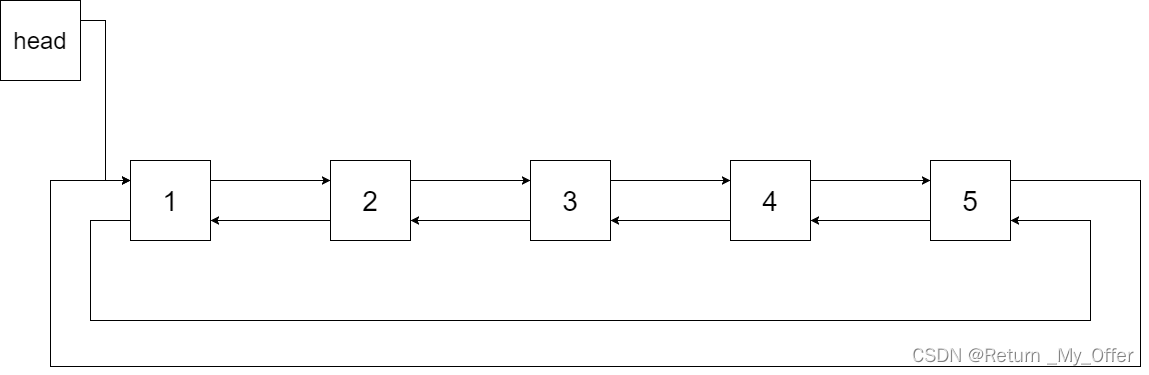
输出：[1,2,3,4,5]
解释：下图显示了转化后的二叉搜索树，实线表示后继关系，虚线表示前驱关系

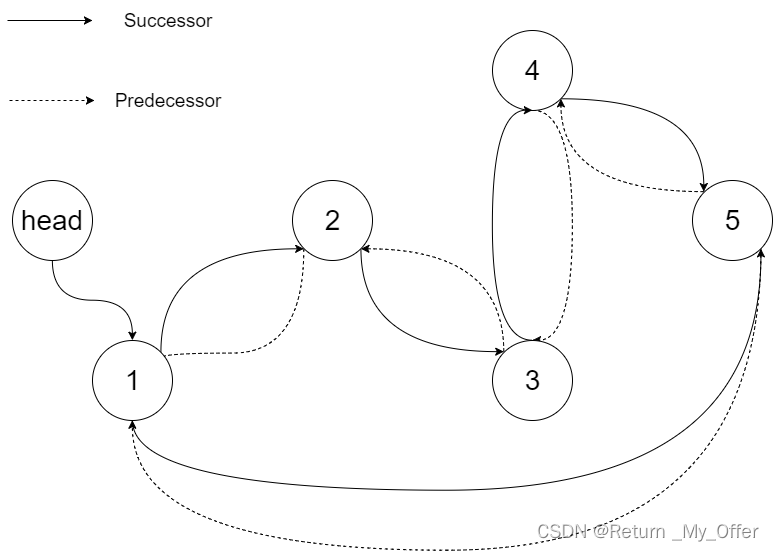
示例 2：
输入：root = [2,1,3]
输出：[1,2,3]
示例 3：
输入：root = []
输出：[]
解释：输入是空树，所以输出也是空链表
示例 4：
输入：root = [1]
输出：[1]
如何遍历树
遍历树的一般策略有两种：
深度优先搜索 (DFS) 在这种策略中，我们将 深度 作为优先级，因此我们从根节点开始，一路搜索到某个叶子节点，然后返回根节点寻找另一条分支。DFS 策略可以进一步区分为 前序，中序 和 后序，这取决于根节点、左节点和右节点之间的相对顺序
广度优先搜索 (BFS) 我们按照高度的顺序，从上到下扫描整棵树 高层级的节点会比低层级的节点先被访问 在下面的图像中，节点按照你访问它们的顺序进行编号，请按照 1-2-3-4-5 的顺序比较不同的策略

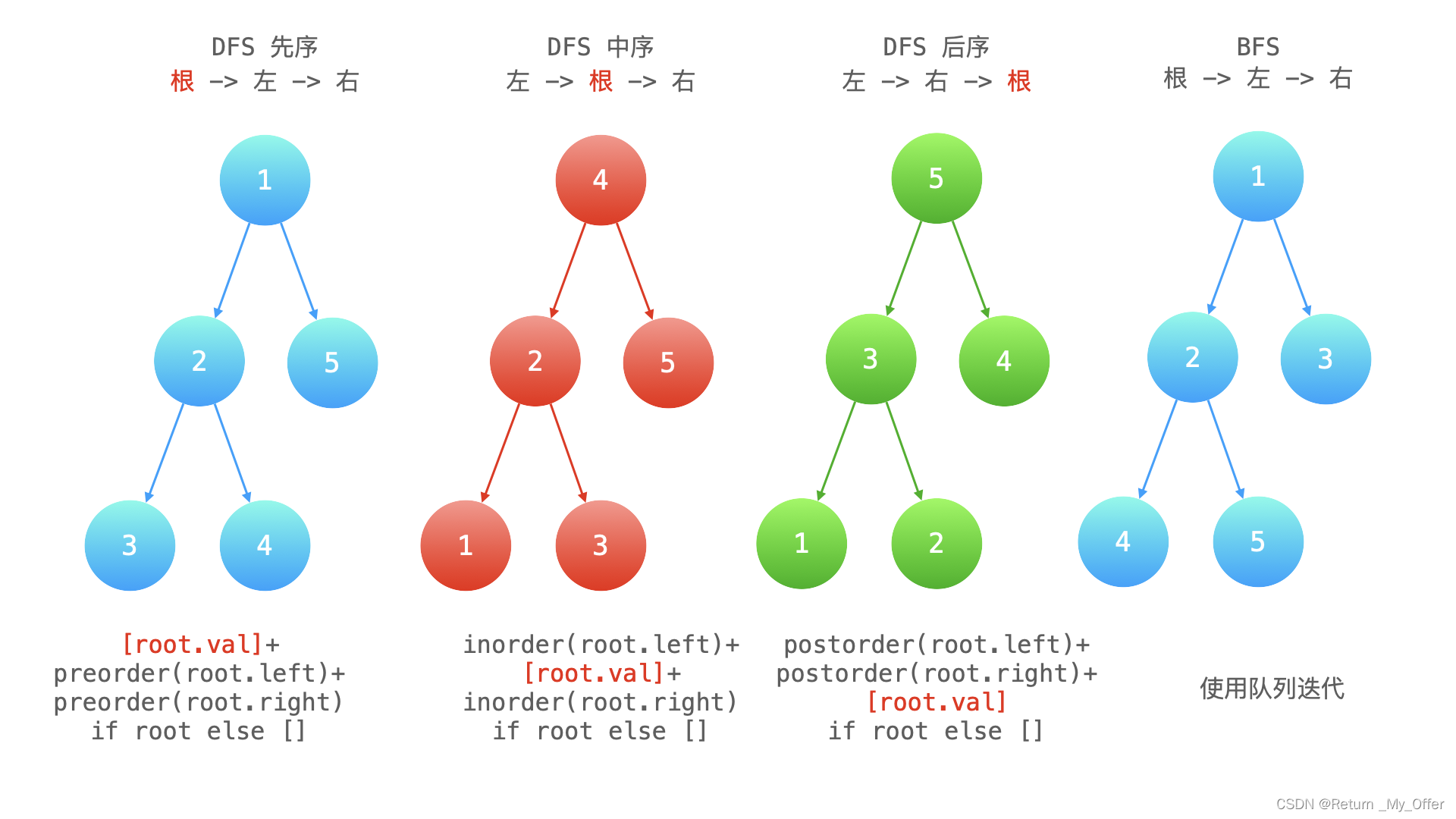
这个问题是以教科书递归方式实现 DFS 中序遍历，因为它要求就地（in-place）操作

方法：递归

算法 标准的中序递归遵循 左 -> 节点 -> 右 的顺序，其中 左 和 右 部分是递归调用，而 节点 是所有处理过程的执行场所。 处理在这里基本上是将前一个节点与当前节点相连，并记录到目前为止新双向链表中的最大节点，亦即最后一个节点
再多一个细节：需要保留第一个，即最小的节点，以封闭双向链表的环。 这是算法的步骤：
初始化 first 和 last 节点为 null
调用标准的中序递归 helper(root) ：
如果节点不为 null：
调用左子树的递归 helper(node.left)
如果 last 节点不为 null，将 last 和当前 node 节点连接起来
若 else，则初始化 first 节点
将当前节点标记为最后一个节点：last = node
调用右子树的递归 helper(node.right)
将首尾两个节点连接起来，封闭 DLL 环，然后返回 first 节点

/*
// Definition for a Node.
struct Node {
    int val;
    struct Node* left;
    struct Node* right;
};
*/
void helper(struct Node*node,struct Node**first,struct Node**last)
{
    if(node){
        helper(node->left,first,last);
        if(*last){
            (*last)->right=node;
            node->left=*last;
            }
        else{
            *first=node;
        }
        *last=node;
        helper(node->right,first,last);
    }
}
struct Node* treeToDoublyList(struct Node *root) {
    struct Node*first=NULL;
    struct Node*last=NULL;
    if(root==NULL)
    {
        return root;
    }
    else
    {
        helper(root,&first,&last);
        last->right=first;
        first->left=last;
    }
    return first;
}