Leetcode 第 360 场周赛题解

题目1：2833. 距离原点最远的点

思路

贪心。

要使得到达的距离原点最远的点，就看 left 和 right 谁大，将 left 和 right 作为矢量相加，再往同方向加上 underline。

答案即为 abs(left - right) + underline。

代码

/*
 * @lc app=leetcode.cn id=2833 lang=cpp
 *
 * [2833] 距离原点最远的点
 */

// @lc code=start
class Solution
{
public:
    int furthestDistanceFromOrigin(string moves)
    {
        int left = 0, right = 0, underline = 0;
        for (char &c : moves)
        {
            if (c == 'L')
                left++;
            else if (c == 'R')
                right++;
            else
                underline++;
        }
        return abs(left - right) + underline;
    }
};
// @lc code=end

复杂度分析

时间复杂度：O(n)，其中 n 是字符串 moves 的长度。

空间复杂度：O(1)。

题目2：2834. 找出美丽数组的最小和

思路

贪心。

从最小正整数 1 开始枚举，设当前数为 num，如果 nums 里没有 target - num，就说明可以添加 num，依次填满直到有 n 个数即可。

用集合 nums 存储数据保证唯一性。

class Solution
{
private:
    const int MOD = 1e9 + 7;

public:
    int minimumPossibleSum(int n, int target)
    {
        set<int> nums;
        nums.insert(1);
        int num = 2;
        while (nums.size() < n)
        {
            if (!nums.count(target - num))
                nums.insert(num);
            num++;
        }
        return accumulate(nums.begin(), nums.end(), 0LL) % MOD;
    }
};

结果超时了：

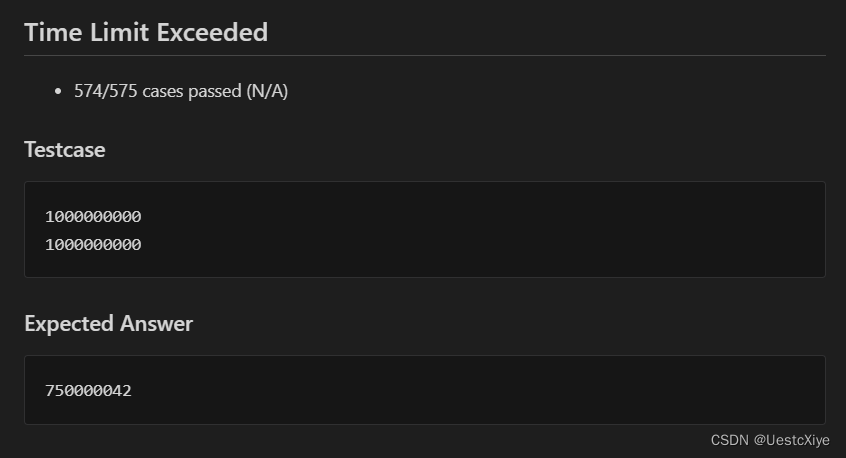
我们发现了规律，对于 [1, target−1] 内的数字：

1. 1 和 target-1 只能选其中一个，为了使美丽数组的总和最小，我们选1。
2. 2 和 target-2 只能选其中一个，为了使美丽数组的总和最小，我们选2。
3. …
4. 一直到 ⌊target/2⌋，无论 target 是奇数还是偶数，它都可以选。

设 m = min(n, ⌊target/2⌋)，我们选择1~m，总和为 m(m+1)/2。

此时还剩下 n-m个数，只能从 target 开始往后选，一直到 target+n-m-1。

代码

/*
 * @lc app=leetcode.cn id=2834 lang=cpp
 *
 * [2834] 找出美丽数组的最小和
 */

// @lc code=start
// class Solution
// {
// private:
//     const int MOD = 1e9 + 7;

// public:
//     int minimumPossibleSum(int n, int target)
//     {
//         set<int> nums;
//         nums.insert(1);
//         int num = 2;
//         while (nums.size() < n)
//         {
//             if (!nums.count(target - num))
//                 nums.insert(num);
//             num++;
//         }
//         return accumulate(nums.begin(), nums.end(), 0LL) % MOD;
//     }
// };

class Solution
{
private:
    const int MOD = 1e9 + 7;

public:
    int minimumPossibleSum(int n, int target)
    {
        long long m = min(target / 2, n);
        return (cal(1, m) + cal(target, target + n - m - 1)) % MOD;
    }
    // 辅函数 - 返回 [left, right] 区间内元素和
    long long cal(int left, int right)
    {
        long long sum = 0;
        for (int i = left; i <= right; i++)
            sum += i;
        return sum;
    }
};
// @lc code=end

复杂度分析

时间复杂度：O(1)。

空间复杂度：O(1)。

题目3：2835. 使子序列的和等于目标的最少操作次数

思路

贪心。

因为每个数最终都能拆成 1，只有当 sum(nums) < target 时才会无解，返回 -1。

剩下的都是有解的情况：

枚举 target 所有为 1 二进制位 i，令 x = 1 << i。

1. 先看 nums 中所有小于 x 的数之和是否大于等于 x，如果是，我们可以用这些数拼出一个 x，那么这个二进制位可以跳过。
2. 否则看 nums 里是否恰好有 x，如果是，那么这个二进制位也可以跳过。
3. 否则只能看 nums 里下一个比 x 大的数，执行若干次操作，拆分得到 x。

贪心的思想体现在：只看 nums 里下一个比 x 大的数，这样的数最接近 x，可以用最少的操作拆分得到 x。

从 target 的低位到高位贪心，将数组 nums 从大到小排序，先消耗较小的元素，拆分得到的数一定比原来的数要小，而且是以递减的顺序添加的，直接插入数组的末尾，不会改变数组递减的性质。

小细节：在y > x那里，为什么每次只push一个y呢，按理说会拆成两个。这是因为一个拆成两个一个会添加到原来的数组中，另一个要么等于x，被使用，要么大于x，要继续被拆，本次不会被添加到原有的数组中。

代码

/*
 * @lc app=leetcode.cn id=2835 lang=cpp
 *
 * [2835] 使子序列的和等于目标的最少操作次数
 */

// @lc code=start
class Solution
{
public:
    int minOperations(vector<int> &nums, int target)
    {
        // 排除无解的情况
        if (accumulate(nums.begin(), nums.end(), 0LL) < target)
            return -1;
        // nums 从大到小排序
        sort(nums.begin(), nums.end(), greater<int>());
        int step = 0;
        // t 表示比当前二进制位小的所有数之和
        long long t = 0;
        for (int i = 0; i < 32; i++)
        {
            // 如果 target 的第 i 位是 1
            if (target >> i & 01)
            {
                int x = 1 << i;
                // 不断把比当前二进制位小的数加到 t 里
                while (!nums.empty() && nums.back() < x && t < x)
                {
                    t += nums.back();
                    nums.pop_back();
                }
                // 比当前二进制位小的数之和已经大于等于当前二进制位，这一位不用操作
                if (t >= x)
                    t -= x;
                // 刚好找到需要的数，也不用操作
                else if (nums.back() == x)
                    nums.pop_back();
                else
                {
                    // 看下一个更大的数，用它拆出当前二进制位
                    int y = nums.back();
                    nums.pop_back();
                    while (y > x)
                    {
                        y >>= 1;
                        // 注意：只有这里会往 nums 的尾部添加数
                        // 由于添加的数都小于原来的尾部，而且是以递减的顺序添加的
                        // 所以 nums 递减的性质不改变
                        nums.push_back(y);
                        step++;
                    }
                }
            }
        }
        return step;
    }
};
// @lc code=end

复杂度分析

时间复杂度：O(nlogn+log(target))，其中 n 是数组 nums 的长度。

空间复杂度：O(log(target))。

题目4：

超出能力范围。

题解：【模板】树上倍增（Python/Java/C++/Go）