2.1.1BFS中的Flood Fill和最短路模型

1.池塘计数

农夫约翰有一片 $N * M$ 的矩形土地。

最近，由于降雨的原因，部分土地被水淹没了。

现在用一个字符矩阵来表示他的土地。

每个单元格内，如果包含雨水，则用”W”表示，如果不含雨水，则用”.”表示。

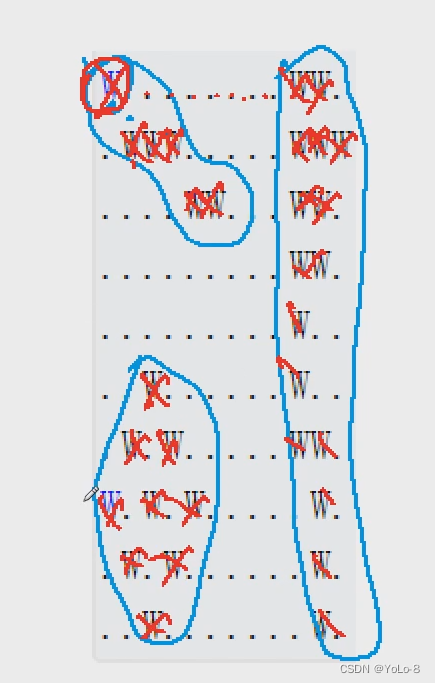
现在，约翰想知道他的土地中形成了多少片池塘。

每组相连的积水单元格集合可以看作是一片池塘。

每个单元格视为与其上、下、左、右、左上、右上、左下、右下八个邻近单元格相连。

请你输出共有多少片池塘，即矩阵中共有多少片相连的”W”块。

输入格式
第一行包含两个整数 $N$ 和 $M$ 。

接下来 $N$ 行，每行包含 $M$ 个字符，字符为”W”或”.”，用以表示矩形土地的积水状况，字符之间没有空格。

输出格式
输出一个整数，表示池塘数目。

数据范围
$1 \leq N, M \leq 1000$

输入样例：

10 12
W........WW.
.WWW.....WWW
....WW...WW.
.........WW.
.........W..
..W......W..
.W.W.....WW.
W.W.W.....W.
.W.W......W.
..W.......W.

输出样例：

1.1题解

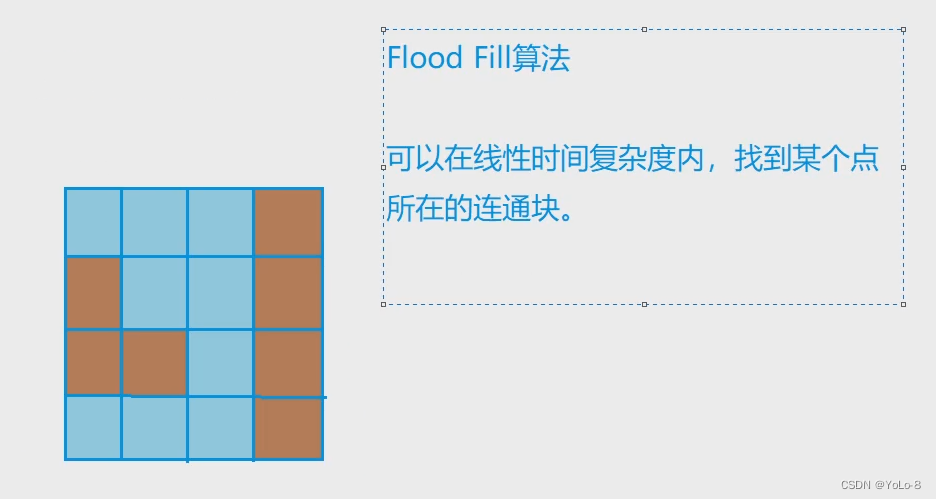
在这里插入图片描述

在这里插入图片描述
bfs

遍历单元格，同时用一个标记数组记录（标记）每个单元格是否被访问过。

在遍历单元格过程中，如果当前单元格是水，并且没有被访问过，水域数量+1，并且对该单元格进行bfs。

bfs 函数：从当前单元格开始，访问并标记和他同一片水域的单元格。

1.2代码实现

#include<iostream>
#include<algorithm>
#include<cstring>

#define x first
#define y second

using namespace std;

//储存下标
typedef pair<int,int> PII;
const int N = 1010,M = N * N;

int n,m;
char g[N][N];
PII q[M];
bool st[N][N]; //判重数组

void bfs(int sx,int sy)
{
    //模拟队列
    int hh = 0,tt = 0;
    q[0] = {sx,sy};
    st[sx][sy] = true;
    
    while(hh <= tt)
    {
        PII t = q[hh++];//取出队头
        //判断8连通，一般使用双重循环
        for(int i = t.x - 1;i <= t.x + 1;i++)
            for(int j = t.y - 1;j <= t.y + 1;j++)
            {
                if(i == t.x && j == t.y)    continue;
                if(i < 0 || i >= n || j < 0 || j >= m)  continue;
                if(g[i][j] == '.' || st[i][j])  continue;
                
                q[++ tt] = {i,j};
                st[i][j] = true;
            }
    }
}


int main()
{
    scanf("%d%d",&n,&m);
    for(int i = 0;i < n;i++)    scanf("%s",g[i]);
    
    int cnt = 0;
    for(int i = 0;i < n;i++)    
        for(int j = 0;j < m;j++)
            if(g[i][j] == 'W' && !st[i][j])
            {
                bfs(i,j);
                cnt++;
            }
    
    printf("%d",cnt);
    
    return 0;
}

2.城堡问题

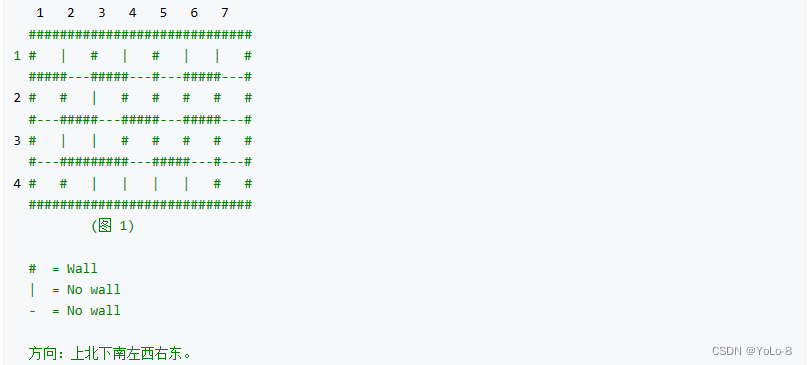
在这里插入图片描述
图1是一个城堡的地形图。

请你编写一个程序，计算城堡一共有多少房间，最大的房间有多大。

城堡被分割成 $m * n$ 个方格区域，每个方格区域可以有 $04$ 面墙。

注意：墙体厚度忽略不计。

输入格式
第一行包含两个整数 $m$ 和 $n$ ，分别表示城堡南北方向的长度和东西方向的长度。

接下来 $m$ 行，每行包含 $n$ 个整数，每个整数都表示平面图对应位置的方块的墙的特征。

每个方块中墙的特征由数字 $P$ 来描述，我们用 $1$ 表示西墙， $2$ 表示北墙， $4$ 表示东墙， $8$ 表示南墙， $P$ 为该方块包含墙的数字之和。

例如，如果一个方块的 $P$ 为 $3$ ，则 $3 = 1 + 2$ ，该方块包含西墙和北墙。

城堡的内墙被计算两次，方块 $(1, 1)$ 的南墙同时也是方块 $(2, 1)$ 的北墙。

输入的数据保证城堡至少有两个房间。

输出格式
共两行，第一行输出房间总数，第二行输出最大房间的面积（方块数）。

数据范围
$1 \leq m, n \leq 50,$
$0 \leq P \leq 15$
输入样例：

4 7 
11 6 11 6 3 10 6 
7 9 6 13 5 15 5 
1 10 12 7 13 7 5 
13 11 10 8 10 12 13

输出样例：

5
9

2.1题解

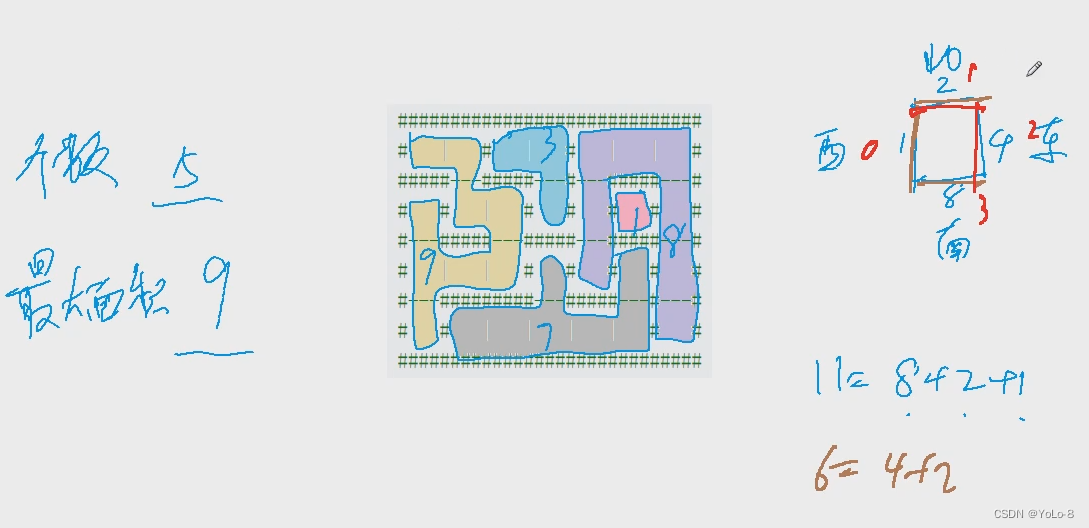
在这里插入图片描述

不过本题中:
西墙表示:1,北墙表示:2,东墙表示:4,南墙表示:8
可以看出依次是 $2^{0},2^{1},2^{2},2^{3}$
所以可以用二进制来表示墙的分布情况.
例如: $0101)_{2}$ 表示南,北边无墙,东,西边有墙

2.2代码实现

#include<iostream>
#include<algorithm>
#include<cstring>

#define x first
#define y second

using namespace std;

typedef pair<int,int> PII;

const int N = 55,M = N * N;

int n,m;
int g[N][N];
PII q[M];
bool st[N][N];

int bfs(int sx,int sy)
{
    //标记一下方向
    int dx[4] = {0,-1,0,1},dy[4] = {-1,0,1,0};
    
    int hh = 0,tt = 0;
    int area = 0;
    q[0] = {sx,sy};
    st[sx][sy] = true;
    
    while(hh <= tt)
    {
        PII t = q[hh++];
        area++;
        //遍历四个方向
        for(int i = 0; i < 4;i++)
        {
            int a = t.x + dx[i],b = t.y + dy[i];
            if(a < 0 || a >= n || b < 0 || b >= m)  continue;
            if(st[a][b])    continue;
            if(g[t.x][t.y] >> i & 1)    continue;
            
            q[++ tt] = {a,b};
            st[a][b] = true;
        }
    }
    
    return area;
}

int main()
{
    cin >> n >> m;
    for(int i = 0;i < n;i++)
        for(int j = 0;j < m;j++)
            cin >> g[i][j];
            
    int cnt = 0,area = 0;
    for(int i = 0;i < n;i++)
        for(int j = 0;j < m;j++)
            if(!st[i][j])
            {
                area = max(area,bfs(i,j));
                cnt++;
            }
            
    cout << cnt << endl;
    cout << area << endl;
    return 0;
}

3.山峰和山谷

FGD小朋友特别喜欢爬山，在爬山的时候他就在研究山峰和山谷。

为了能够对旅程有一个安排，他想知道山峰和山谷的数量。

给定一个地图，为FGD想要旅行的区域，地图被分为 $n \times n$ 的网格，每个格子 $(i, j)$ 的高度 $w (i, j)$ 是给定的。

若两个格子有公共顶点，那么它们就是相邻的格子，如与 $(i, j)$ 相邻的格子有 $(i - 1, j - 1), (i - 1, j), (i - 1, j + 1), (i, j - 1), (i, j + 1), (i + 1, j - 1), (i + 1, j), (i + 1, j + 1)$ 。

我们定义一个格子的集合 $S$ 为山峰（山谷）当且仅当：

$S$ 的所有格子都有相同的高度。
$S$ 的所有格子都连通。
对于 $s$ 属于 $S$ ，与 $s$ 相邻的 $s^{'}$ 不属于 $S$ ，都有 $w_{s}>w_{s^{'}}$ （山峰），或者 $w_{s}<w_{s^{'}}$ （山谷）。
如果周围不存在相邻区域，则同时将其视为山峰和山谷。

你的任务是，对于给定的地图，求出山峰和山谷的数量，如果所有格子都有相同的高度，那么整个地图即是山峰，又是山谷。

输入格式
第一行包含一个正整数 $n$ ，表示地图的大小。

接下来一个 $n \times n$ 的矩阵，表示地图上每个格子的高度 $w$ 。

输出格式
共一行，包含两个整数，表示山峰和山谷的数量。

数据范围
$1 \leq n \leq 1000,$
$0≤w≤10^{9}$

输入样例1：

输出样例1：

2 1

输入样例2：

输出样例2：

3 3

样例解释
样例1：

样例2：

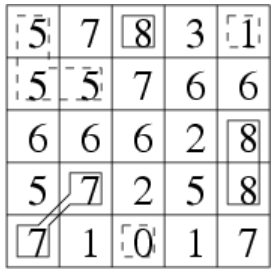
3.1题解

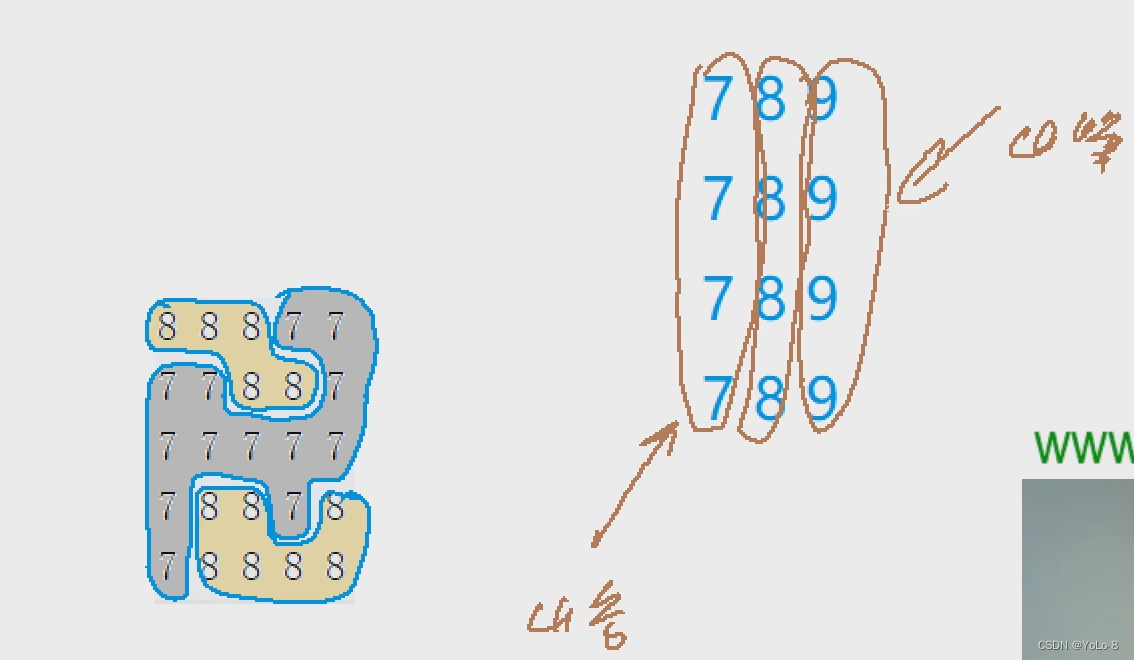
在这里插入图片描述

3.2代码

#include<cstring>
#include<iostream>
#include<algorithm>

#define x first
#define y second

using namespace std;

typedef pair<int,int> PII;

const int N = 1010,M = N * N;

int n;
int h[N][N];
PII q[M];
bool st[N][N];


//引用，在此传进去的参数是引用
void bfs(int sx,int sy,bool& has_higher,bool& has_lower)
{
    int hh = 0,tt = 0;
    q[0] = {sx,sy};
    st[sx][sy] = true;
    
    while(hh <= tt)
    {
        PII t = q[hh++];
        //八连接，使用双重循环
        for(int i = t.x - 1;i <= t.x + 1;i++)
            for(int j = t.y - 1;j <= t.y + 1;j++)
            {
                if(i == t.x && j == t.y) continue;//把中间格子扣掉
                if(i < 0 || i >= n || j < 0 || j >= n)  continue;
                if(h[i][j] != h[t.x][t.y])  //山脉的边界
                {
                    if(h[i][j] > h[t.x][t.y])   has_higher = true;
                    else has_lower = true;
                }
                else if(!st[i][j])
                {
                    q[++ tt] = {i,j};
                    st[i][j] = true;
                }
            }
    }
}
int main()
{
    scanf("%d",&n);
    
    for(int i = 0;i < n;i++)
        for(int j = 0;j < n;j++)
            scanf("%d",&h[i][j]);
            
    int peak = 0,valley = 0;
    for(int i = 0;i < n;i++)
        for(int j = 0;j < n;j++)
            if(!st[i][j])
            {
                bool has_higher = false,has_lower = false;
                //使用传引用的方式
                bfs(i,j,has_higher,has_lower);
                if(!has_higher) peak++;
                //注意在此不能单纯的使用else，因为有可能即是山峰又是山谷
                if(!has_lower)  valley++;
            }
            
    printf("%d %d\n",peak,valley);
    
    return 0;
}

4.迷宫问题

给定一个 $n \times n$ 的二维数组，如下所示：

int maze[5][5] = {

0, 1, 0, 0, 0,

0, 1, 0, 1, 0,

0, 0, 0, 0, 0,

0, 1, 1, 1, 0,

0, 0, 0, 1, 0,

};

它表示一个迷宫，其中的 $1$ 表示墙壁， $0$ 表示可以走的路，只能横着走或竖着走，不能斜着走，要求编程序找出从左上角到右下角的最短路线。

数据保证至少存在一条从左上角走到右下角的路径。

输入格式
第一行包含整数 $n$ 。

接下来 $n$ 行，每行包含 $n$ 个整数 $0$ 或 $1$ ，表示迷宫。

输出格式
输出从左上角到右下角的最短路线，如果答案不唯一，输出任意一条路径均可。

按顺序，每行输出一个路径中经过的单元格的坐标，左上角坐标为 $(0, 0)$ ，右下角坐标为 $(n - 1, n - 1)$ 。

数据范围
$0 \leq n \leq 1000$
输入样例：

输出样例：

4.1题解

这道题是844题的扩展我们这道题是想让我们将最短的路进行输出
我们的做法是用 $p re [] []$ 数组来记录当前结点前驱结点是哪个点以便我们输出它最短路径的坐标点我们倒着寻找最短路径从 $(n - 1, n - 1)$ 开始
这样的话更新完 $p re$ 数组 $(0, 0)$ 就有它的前驱结点了这样就能正着将 $p re$ 数组中输出对应的路径了
关键和844的不同点就是如何维护 $p re$ 这个记录路径的数组以及你如何将这个数组数组也是有学问的

4.2代码

#include<cstring>
#include<algorithm>
#include<iostream>

#define x first
#define y second

using namespace std;

typedef pair<int,int> PII;

const int N = 1010,M = N * N;

int n;
int g[N][N];
PII q[M];
PII pre[N][N];  //记录路径

void bfs(int sx,int sy)
{
    //四个方向，上右下左
    int dx[4] = {-1,0,1,0},dy[4] = {0,1,0,-1};
    int hh = 0,tt = 0;
    q[0] = {sx,sy};
    
    memset(pre,-1,sizeof pre);
    pre[sx][sy] = {0,0};
    while(hh <= tt)
    {
        PII t = q[hh ++];
        
        for(int i = 0;i < 4;i++)
        {
            int a = t.x + dx[i],b = t.y + dy[i];
            if(a < 0 || a >= n || b < 0 || b >= n)  continue;
            if(g[a][b]) continue;
            if(pre[a][b].x != -1)   continue;
            
            q[++ tt] = {a,b};
            pre[a][b] = t;
        }
    }
}
int main()
{
    scanf("%d",&n);
    
    for(int i = 0;i < n;i++)
        for(int j = 0;j < n;j++)
            scanf("%d",&g[i][j]);
    //反向搜        
    bfs(n - 1,n - 1);
    
    PII end(0,0);
    
    while(true)
    {
        printf("%d %d\n",end.x,end.y);
        if(end.x == n - 1 && end.y == n - 1)    break;
        end = pre[end.x][end.y];
    }
    
    return 0;
    
}

5.武士风度的牛

农民 $J o hn$ 有很多牛，他想交易其中一头被 $Do n$ 称为 $T h eK ni g h t$ 的牛。

这头牛有一个独一无二的超能力，在农场里像 $K ni g h t$ 一样地跳（就是我们熟悉的象棋中马的走法）。

虽然这头神奇的牛不能跳到树上和石头上，但是它可以在牧场上随意跳，我们把牧场用一个 $x ， y$ 的坐标图来表示。

这头神奇的牛像其它牛一样喜欢吃草，给你一张地图，上面标注了 $T h eK ni g h t$ 的开始位置，树、灌木、石头以及其它障碍的位置，除此之外还有一捆草。

现在你的任务是，确定 $T h eK ni g h t$ 要想吃到草，至少需要跳多少次。

$T h eK ni g h t$ 的位置用 K 来标记，障碍的位置用 * 来标记，草的位置用 H 来标记。

这里有一个地图的例子：

             11 | . . . . . . . . . .
             10 | . . . . * . . . . . 
              9 | . . . . . . . . . . 
              8 | . . . * . * . . . . 
              7 | . . . . . . . * . . 
              6 | . . * . . * . . . H 
              5 | * . . . . . . . . . 
              4 | . . . * . . . * . . 
              3 | . K . . . . . . . . 
              2 | . . . * . . . . . * 
              1 | . . * . . . . * . . 
              0 ----------------------
                                    1 
                0 1 2 3 4 5 6 7 8 9 0

$T h eK ni g h t$ 可以按照下图中的 $A, B, C, D \dots$ 这条路径用 $5$ 次跳到草的地方（有可能其它路线的长度也是 $5$ ）:

             11 | . . . . . . . . . .
             10 | . . . . * . . . . .
              9 | . . . . . . . . . .
              8 | . . . * . * . . . .
              7 | . . . . . . . * . .
              6 | . . * . . * . . . F<
              5 | * . B . . . . . . .
              4 | . . . * C . . * E .
              3 | .>A . . . . D . . .
              2 | . . . * . . . . . *
              1 | . . * . . . . * . .
              0 ----------------------
                                    1
                0 1 2 3 4 5 6 7 8 9 0

注意：数据保证一定有解。

输入格式
第 $1$ 行：两个数，表示农场的列数 $C$ 和行数 $R$ 。

第 $2.. R + 1$ 行: 每行一个由 $C$ 个字符组成的字符串，共同描绘出牧场地图。

输出格式
一个整数，表示跳跃的最小次数。

数据范围
$1 \leq R, C \leq 150$
输入样例：

10 11
..........
....*.....
..........
...*.*....
.......*..
..*..*...H
*.........
...*...*..
.K........
...*.....*
..*....*..

输出样例：

5.1题解

广度优先搜索
一般来说走迷宫,最少步数这种题目,都是广度优先搜索.记住读入上面的有梗,然后修改一下一般走路方式就好了.

5.2代码实现

#include<cstring>
#include<iostream>
#include<algorithm>

#define x first
#define y second

using namespace std;

typedef pair<int,int> PII;
const int N = 155,M = N * N;

int n,m;
char g[N][N];
PII q[M];
int dist[N][N];//存储最短路

int bfs()
{
    int dx[8] = {-2,-1,1,2,2,1,-1,-2};
    int dy[8] = {1,2,2,1,-1,-2,-2,-1};
    int sx,sy;
    //寻找起点
    for(int i = 0;i < n;i++)
        for(int j = 0;j < m;j++)
            if(g[i][j] == 'K')
                sx = i,sy = j;
                
    int hh = 0,tt = 0;
    q[0] = {sx,sy};
    
    memset(dist,-1,sizeof dist);
    dist[sx][sy] = 0;
    
    while(hh <= tt)
    {
        auto t = q[hh ++];
        
        for(int i = 0;i < 8;i++)
        {
            int a = t.x + dx[i], b = t.y + dy[i];
            if(a < 0 || a >= n || b < 0 || b >= m) continue;//不在范围内
            if(g[a][b] == '*')  continue;//是障碍物
            if(dist[a][b] != -1)    continue;//不是第一次被访问
            if(g[a][b] == 'H')  return dist[t.x][t.y] + 1;
            
            dist[a][b] = dist[t.x][t.y] + 1;
            q[++ tt] = {a,b};
        }
    }
    
    return -1;
}
int main()
{
    cin >> m >> n;
    
    for(int i = 0;i < n;i++)    cin >> g [i];
    
    cout << bfs() <<endl;
    
    return 0;
    
}

6.抓住那头牛

农夫知道一头牛的位置，想要抓住它。

农夫和牛都位于数轴上，农夫起始位于点 $N$ ，牛位于点 $K$ 。

农夫有两种移动方式：

从 $X$ 移动到 $X - 1$ 或 $X + 1$ ，每次移动花费一分钟
从 $X$ 移动到 $2 * X$ ，每次移动花费一分钟

假设牛没有意识到农夫的行动，站在原地不动。

农夫最少要花多少时间才能抓住牛？

输入格式
共一行，包含两个整数 $N$ 和 $K$ 。

输出格式
输出一个整数，表示抓到牛所花费的最少时间。

数据范围
$0≤N,K≤10^{5}$
输入样例：

5 17

输出样例：

5.1题解

看完题目以后，农夫不就是向右移动{-1,1，当前位置}这三种情况吗，
于是就普通至极，至于范围的话，
如果 $k==1e^{5},n>50000$ 时，实际上最短步数一定只有两种情况：

如果 $n - 50000 < k - n$ 时，就会后退到 $50000$ 再 $* 2$
否则就一直 $+ 1$ 到 $k$

范围就是 $0<=n<=1e^{5}$

5.2代码

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1e5 + 10;

int n, k;
int q[N];
int dist[N];

int bfs()
{
    memset(dist, -1, sizeof dist);
    dist[n] = 0;
    q[0] = n;

    int hh = 0, tt = 0;

    while (hh <= tt)
    {
        int t = q[hh ++ ];

        if (t == k) return dist[k];

        if (t + 1 < N && dist[t + 1] == -1)
        {
            dist[t + 1] = dist[t] + 1;
            q[ ++ tt] = t + 1;
        }
        if (t - 1 >= 0 && dist[t - 1] == -1)
        {
            dist[t - 1] = dist[t] + 1;
            q[ ++ tt] = t - 1;
        }
        if (t * 2 < N && dist[t * 2] == -1)
        {
            dist[t * 2] = dist[t] + 1;
            q[ ++ tt] = t * 2;
        }
    }

    return -1;
}

int main()
{
    cin >> n >> k;

    cout << bfs() << endl;

    return 0;
}