遗传算法求解旅行商问题（含python源代码）

前言

编码初始化种群

计算适应度

选择

交叉

变异

完整代码

总结

前言

这次的算法有一点不能确定是否正确，希望有大佬能够批评指正。

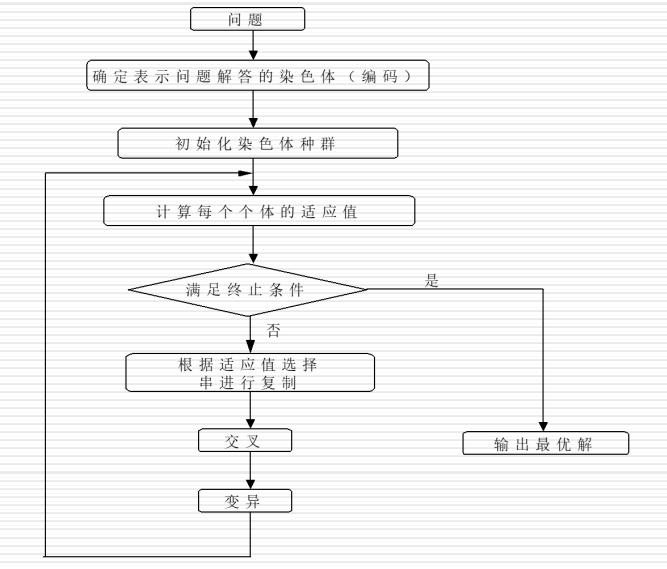
遗传算法的一般步骤

编码初始化种群

种群（population）指同一时间生活在一定自然区域内，同种生物的所有个体。

所以种群是由个体组成的，所以先需要得到个体，然后再随机产生一定数目的个体。

在本算法中个体采用的是实数编码。

先对城市的位置进行初始化，采用的是用列表来表示城市的坐标，可以单个定义，也可以随机生成。

先生成一串有序的数字用来表示城市的编号，再每次随机进行打乱后储存到pop列表中，pop表示种群，里面装着的是列表用来表示个体。（个体表示城市的编号，种群表示编号打乱后个体的集合）

群体规模太小，不能提供足够的采样点,以致算法性能很差，易陷入局部最优解。

群体规模太大，尽管可以增加优化信息,阻止早熟收敛的发生,但无疑会增加计算量,造成收敛时间太长,表现为收敛速度缓慢。

City_Map = 100 * np.random.rand(20, 2)  # 随机产生20个城市（20行2列，数值乘以100)
DNA_SIZE = len(City_Map)  # 编码长度（返回行的个数)
POP_SIZE = 100  # 种群大小
# 生成初代种群pop
pop = []
list = list(range(DNA_SIZE))  # 生成[0,DNA_SIZE)的列表
for i in range(POP_SIZE):  # POP_SIZE是指种群大小，在程序中是一个固定的值(打乱POP_SIZE次之后把结果储存到pop列表中
    random.shuffle(list)  # 随机打乱list，进行初始化操作
    l = list.copy()  # 把list中的数据拷贝到l中
    pop.append(l)  # 将l添加到pop列表中

计算适应度

适应度函数值只能是正值，越大越好。

DNA表示个体，根据个体的值（表示城市的编号）来计算距离。

旅行商问题要求距离越短越好，所以距离越大越不满足要求，故而可以通过对距离求倒数来表示适应度。

在最后减去适应度最小的值，可以保证适应度都为正值。（如果有负数，减去一个更小的负数，会变成正值）

def distance(DNA):  # 根据DNA的路线计算距离
    dis = 0
    temp = City_Map[DNA[0]]
    for i in DNA[1:]:
        # sqrt(pow(x-x0,2)+pow(y-y0,2))
        dis = dis + ((City_Map[i][0] - temp[0]) ** 2 + (City_Map[i][1] - temp[1]) ** 2) ** 0.5
        temp = City_Map[i]
    return dis + ((temp[0] - City_Map[DNA[0]][0]) ** 2 + (temp[1] - City_Map[DNA[0]][1]) ** 2) ** 0.5


def getfitness(pop):  # 计算种群适应度，这里适应度用距离的倒数表示
    temp = []
    for i in range(len(pop)):
        temp.append(1 / (distance(pop[i])))
    # 减去最小值是为了防止适应度出现负值
    return temp - np.min(temp)

选择

选择操作也称为复制（ reproduction）操作：从当前群体中按照一定概率选出优良的个体，使它们有机会作为父代繁殖下一代子孙。
判断个体优良与否的准则是各个个体的适应度值：个体适应度越高，其被选择的机会就越多。

在程序中个体的选择方法采用的是轮盘赌的方法：

按个体的选择概率产生一个轮盘，轮盘每个区的角度与个体的选择概率成比例。
产生一个随机数，它落入转盘的哪个区域就选择相应的个体交叉
适应度的小的个体也有可能被选中。

def select(pop, fitness):  # 根据适应度选择，以赌轮盘的形式，适应度越大的个体被选中的概率越大
    # print(fitness)
    s = fitness.sum()
    # np.random.choice(a,size,replace,p=None)随机抽取样本a,表示范围，replace=True被抽中后仍有机会被再次抽中，p没抽中的概率
    temp = np.random.choice(np.arange(len(pop)), size=POP_SIZE, replace=True, p=(fitness / s))
    p = []
    for i in temp:
        p.append(pop[i])

    return p

交叉

程序中交叉采用部分匹配交叉，如果直接采用两点交叉会导致一个个体中出现两个重复的城市。

部分匹配交叉保证了每个染色体中的基因仅出现一次，通过该交叉策略在一个染色体中不会出现重复的基因，所以部分匹配交叉经常用于旅行商（TSP）或其他排序问题编码。部分匹配交叉类似于两点交叉，通过随机选择两个交叉点确定交叉区域。执行交叉后一般会得到两个无效的染色体，个别基因会出现重复的情况，为了修复染色体，可以在交叉区域内建立每个染色体的匹配关系，然后在交叉区域外对重复基因应用此匹配关系就可以消除冲突。

交叉概率太大时,种群中个体更新很快,会造成高适应度值的个体很快被破坏掉;

概率太小时,交叉操作很少进行,从而会使搜索停滞不前,造成算法的不收敛。

def crossmuta(pop, CROSS_RATE):  # 交叉变异
    new_pop = []
    for i in range(len(pop)):  # 遍历种群中的每一个个体，将该个体作为父代
        n = np.random.rand()
        if n >= CROSS_RATE:  # 大于交叉概率时不发生变异，该子代直接进入下一代
            temp = pop[i].copy()
            new_pop.append(temp)  # 直接进行拷贝

        if n < CROSS_RATE:  # 小于交叉概率时发生变异
            list1 = pop[i].copy()
            list2 = pop[np.random.randint(POP_SIZE)].copy()  # 选取种群中另一个个体进行交叉(随机选择)
            status = True
            while status:  # 产生2个不相等的节点，中间部分作为交叉段，采用部分匹配交叉(直到k1<k2的时候才会跳出循环)
                k1 = random.randint(0, len(list1) - 1)
                k2 = random.randint(0, len(list2) - 1)
                if k1 < k2:
                    status = False

            k11 = k1  # 保存切片起始的下标

            # 先对部分片段进行切片，把切片出来的内容进行交换（完全交换)
            fragment1 = list1[k1: k2]
            fragment2 = list2[k1: k2]

            list1[k1: k2] = fragment2
            list2[k1: k2] = fragment1

            del list1[k1: k2]  # 删除list1中[k1,k2)的内容
            left1 = list1

            # 进行部分匹配的交叉
            offspring1 = []#后代
            #对left1中的每一个位置pos遍历
            for pos in left1:
                #检查它是否存在于frag2中
                if pos in fragment2:
                    #从fragment1中找到对应的基因
                    pos = fragment1[fragment2.index(pos)]
                    #直到基因不再fragment2中为止（遍历fragment2，确保每一个基因都和pos不同)
                    while pos in fragment2:
                        pos = fragment1[fragment2.index(pos)]
                    offspring1.append(pos)
                    continue
                #如何pos不存在fragment2中，那么就直接将其添加到新的后代中
                offspring1.append(pos)
            # 插入新片段
            for i in range(0, len(fragment2)):
                offspring1.insert(k11, fragment2[i])
                k11 += 1
            temp = offspring1.copy()

            mutation(temp, MUTA_RATE)  # 进行变异

            new_pop.append(temp)  # 把部分匹配交叉后形成的合法个体加入到下一代种群

    return new_pop

变异

互换变异：随机选取染色体的两个基因进行简单互换。
采用随机的形式，在[0,DNA_SIZE)的范围内生成两个下标（确保两个位置不一致），在将两个位置上面的值进行交换。

变异概率太小则很难产生新模式,变异概率太大则会使遗传算法成为随机搜索算法。

def mutation(DNA, MUTA_RATE):  # 进行变异
    # 两点变异
    if np.random.rand() < MUTA_RATE:  # 以MUTA_RATE的概率进行变异
        mutate_point1 = np.random.randint(0, DNA_SIZE)  # 随机产生一个实数，代表要变异基因的位置
        mutate_point2 = np.random.randint(0, DNA_SIZE)  # 随机产生一个实数，代表要变异基因的位置
        while (mutate_point1 == mutate_point2):  # 保证2个所选位置不相等
            mutate_point2 = np.random.randint(0, DNA_SIZE)  #如果相等将mutate_point2重新进行随机生成位置
        DNA[mutate_point1], DNA[mutate_point2] = DNA[mutate_point2], DNA[mutate_point1]  # 2个所选位置进行互换

逆转变异：在个体码串中随机选择两点（逆转点），然后将两点之间的基因值以逆向排序插入到原位置中。

随机生成两个下标，如x1，x2（确保x1<x2），对列表进行[x1,x2)的切片，在原始的列表中删除切片的部分，将切片的部分翻转之后添加到原始的位置。

def mutation(DNA, MUTA_RATE):  # 进行变异
    # 逆转变异
    if np.random.rand() < MUTA_RATE:  # 以MUTA_RATE的概率进行变异
        status = True
        while status:  # 产生2个不相等的节点，中间部分作为交叉段，采用部分匹配交叉(直到mutate_point1<mutate_point2的时候才会跳出循环)
            mutate_point1 = np.random.randint(0, DNA_SIZE)  # 随机产生一个实数，代表要变异基因片段的起始的位置
            mutate_point2 = np.random.randint(0, DNA_SIZE)  # 随机产生一个实数，代表要变异基因片段的结束的位置
            if mutate_point1 < mutate_point2:
                status = False

        k1 = mutate_point1  # 保存切片起始的下标
        temp = DNA[mutate_point1:mutate_point2]  # 把需要逆转的片段先提取出来
        del DNA[mutate_point1:mutate_point2]  # 先暂时删除这段片段
        temp.reverse()  # 反转基因序列
        # 插入翻转后的新片段
        for i in range(0, len(temp)):
            DNA.insert(k1, temp[i])
            k1 += 1

插入变异：在个体码串中随机选择一个码，然后将此码插入随机选择的插入点中间。

随机生成两个实数，这次不是交换，是插入的方式，也就是插入点之后的元素的位置都会发生改变。

def mutation(DNA, MUTA_RATE):  # 进行变异
    #插入变异
    if np.random.rand() < MUTA_RATE:  # 以MUTA_RATE的概率进行变异
        mutate_point1 = np.random.randint(0, DNA_SIZE)  # 随机产生一个实数，代表要变异基因的位置（选中一个基因）
        mutate_point2 = np.random.randint(0, DNA_SIZE)  # 随机产生一个实数，代表要变异基因的位置（插入点）
        while (mutate_point1 == mutate_point2):  # 保证2个所选位置不相等
            mutate_point2 = np.random.randint(0, DNA_SIZE)

        temp=DNA[mutate_point1]#先保存mutate_point1对应的值
        del DNA[mutate_point1]#删除mutate_point1对应的值
        DNA.insert(mutate_point2,temp)#重新插入到列表中

完整代码

import time
import numpy as np
import random
import matplotlib.pyplot as plt

# 各个城市的坐标
City_Map = 100 * np.random.rand(10, 2)  # 随机产生20个城市（20行2列，数值乘以100)

DNA_SIZE = len(City_Map)  # 编码长度（返回行的个数)
POP_SIZE = 100  # 种群大小
CROSS_RATE = 0.85  # 交叉率
MUTA_RATE = 0.15  # 变异率
Iterations = 500  # 迭代次数


def distance(DNA):  # 根据DNA的路线计算距离
    dis = 0
    temp = City_Map[DNA[0]]
    for i in DNA[1:]:
        # sqrt(pow(x-x0,2)+pow(y-y0,2))
        dis = dis + ((City_Map[i][0] - temp[0]) ** 2 + (City_Map[i][1] - temp[1]) ** 2) ** 0.5
        temp = City_Map[i]
    return dis + ((temp[0] - City_Map[DNA[0]][0]) ** 2 + (temp[1] - City_Map[DNA[0]][1]) ** 2) ** 0.5


def getfitness(pop):  # 计算种群适应度，这里适应度用距离的倒数表示
    temp = []
    for i in range(len(pop)):
        temp.append(1 / (distance(pop[i])))
    # 减去最小值是为了防止适应度出现负值
    return temp - np.min(temp)


def select(pop, fitness):  # 根据适应度选择，以赌轮盘的形式，适应度越大的个体被选中的概率越大
    # print(fitness)
    s = fitness.sum()
    # np.random.choice(a,size,replace,p=None)随机抽取样本a,表示范围，replace=True被抽中后仍有机会被再次抽中，p没抽中的概率
    temp = np.random.choice(np.arange(len(pop)), size=POP_SIZE, replace=True, p=(fitness / s))
    p = []
    for i in temp:
        p.append(pop[i])

    return p


def mutation(DNA, MUTA_RATE):  # 进行变异
    # 两点变异
    if np.random.rand() < MUTA_RATE:  # 以MUTA_RATE的概率进行变异
        mutate_point1 = np.random.randint(0, DNA_SIZE)  # 随机产生一个实数，代表要变异基因的位置
        mutate_point2 = np.random.randint(0, DNA_SIZE)  # 随机产生一个实数，代表要变异基因的位置
        while (mutate_point1 == mutate_point2):  # 保证2个所选位置不相等
            mutate_point2 = np.random.randint(0, DNA_SIZE)  #如果相等将mutate_point2重新进行随机生成位置
        DNA[mutate_point1], DNA[mutate_point2] = DNA[mutate_point2], DNA[mutate_point1]  # 2个所选位置进行互换
    

def crossmuta(pop, CROSS_RATE):  # 交叉变异
    new_pop = []
    for i in range(len(pop)):  # 遍历种群中的每一个个体，将该个体作为父代
        n = np.random.rand()
        if n >= CROSS_RATE:  # 大于交叉概率时不发生变异，该子代直接进入下一代
            temp = pop[i].copy()
            new_pop.append(temp)  # 直接进行拷贝

        if n < CROSS_RATE:  # 小于交叉概率时发生变异
            list1 = pop[i].copy()
            list2 = pop[np.random.randint(POP_SIZE)].copy()  # 选取种群中另一个个体进行交叉(随机选择)
            status = True
            while status:  # 产生2个不相等的节点，中间部分作为交叉段，采用部分匹配交叉(直到k1<k2的时候才会跳出循环)
                k1 = random.randint(0, len(list1) - 1)
                k2 = random.randint(0, len(list2) - 1)
                if k1 < k2:
                    status = False

            k11 = k1  # 保存切片起始的下标

            # 先对部分片段进行切片，把切片出来的内容进行交换（完全交换)
            fragment1 = list1[k1: k2]
            fragment2 = list2[k1: k2]

            list1[k1: k2] = fragment2
            list2[k1: k2] = fragment1

            del list1[k1: k2]  # 删除list1中[k1,k2)的内容
            left1 = list1

            # 进行部分匹配的交叉
            offspring1 = []#后代
            #对left1中的每一个位置pos遍历
            for pos in left1:
                #检查它是否存在于frag2中
                if pos in fragment2:
                    #从fragment1中找到对应的基因
                    pos = fragment1[fragment2.index(pos)]
                    #直到基因不再fragment2中为止（遍历fragment2，确保每一个基因都和pos不同)
                    while pos in fragment2:
                        pos = fragment1[fragment2.index(pos)]
                    offspring1.append(pos)
                    continue
                #如何pos不存在fragment2中，那么就直接将其添加到新的后代中
                offspring1.append(pos)
            # 插入新片段
            for i in range(0, len(fragment2)):
                offspring1.insert(k11, fragment2[i])
                k11 += 1
            temp = offspring1.copy()

            mutation(temp, MUTA_RATE)  # 进行变异

            new_pop.append(temp)  # 把部分匹配交叉后形成的合法个体加入到下一代种群

    return new_pop


def print_info(pop):  # 用于输出结果
    fitness = getfitness(pop)
    maxfitness = np.argmax(fitness)  # 得到种群中最大适应度个体的索引
    # 打印结果
    print("最优的基因型：", pop[maxfitness])
    print("最短距离：", distance(pop[maxfitness]))
    # 按最优结果顺序把地图上的点加入到best_map列表中
    best_map = []
    for i in pop[maxfitness]:
        best_map.append(City_Map[i])
    best_map.append(City_Map[pop[maxfitness][0]])
    X = np.array((best_map))[:, 0]
    Y = np.array((best_map))[:, 1]
    # 绘制地图以及路线
    plt.figure()
    plt.rcParams['font.sans-serif'] = ['SimHei']
    plt.scatter(X, Y)
    for dot in range(len(X) - 1):
        plt.annotate(pop[maxfitness][dot], xy=(X[dot], Y[dot]), xytext=(X[dot], Y[dot]))
    plt.annotate('start', xy=(X[0], Y[0]), xytext=(X[0] + 1, Y[0]))
    plt.plot(X, Y)


if __name__ == "__main__":  # 主循环
    # 生成初代种群pop
    pop = []
    list = list(range(DNA_SIZE))  # 生成[0,DNA_SIZE)的列表
    for i in range(POP_SIZE):  # POP_SIZE是指种群大小，在程序中是一个固定的值(打乱POP_SIZE次之后把结果储存到pop列表中
        random.shuffle(list)  # 随机打乱list，进行初始化操作
        l = list.copy()  # 把list中的数据拷贝到l中
        pop.append(l)  # 将l添加到pop列表中
    best_dis = []
    # 最好适应度
    #goodFitness = 0
    # 最差适应度（如果进行归一化处理之后，适应度都减去最小值，那么他的最差适应度不都就是0了)
    #chaFitness = 0
    # 总体适应度
    #sumFitness = 0
    # 所有数量
    #sumCount = 0
    # 平均适应度
    #averageFitness = 0

    # 获取当前时间(算法开始时间)
    start_time = time.time()

    # 进行选择，交叉，变异，并把每代的最优个体保存在best_dis中
    for i in range(Iterations):  # 迭代N代
        pop = crossmuta(pop, CROSS_RATE)  # CROSS_RATE交叉率
        fitness = getfitness(pop)  # 得到适应度种群的适应度
        # 更新最差适应度
        # print(np.min(fitness))
        tmpfitness = np.max(fitness)

        # 更新最好适应度
        #if tmpfitness > goodFitness:
        #    goodFitness = tmpfitness
        # print(goodFitness)

        # 记录所有适应度的值
        #sumFitness = np.sum(fitness) + sumFitness
        # 记录所有适应度的个数
        #sumCount = sumCount + np.size(fitness)

        maxfitness = np.argmax(fitness)  # 返回数值最大的索引
        best_dis.append(distance(pop[maxfitness]))
        pop = select(pop, fitness)  # 选择生成新的种群（适应度最大的)
        print("iteration", i)

    #averageFitness = sumFitness / sumCount
    # 获取当前时间(算法结束时间)
    end_time = time.time()

    print_info(pop)  # 打印信息

    print('逐代的最小距离：', best_dis)
    #print(f'最好适应度：{goodFitness:.4f}')
    #print(f'最差适应度：{chaFitness:.4f}')
    #print(f'平均适应度：{averageFitness:.4f}')
    print(f'程序运行时间：{(end_time - start_time):.4f}秒')
    #print(pop)


# 画图
plt.figure()
plt.plot(range(Iterations), best_dis)
plt.show()
plt.close()

参考信息

遗传算法入门详解 - 知乎 (zhihu.com)https://zhuanlan.zhihu.com/p/100337680遗传算法python进阶理解+论文复现（纯干货，附前人总结引路）_python神经网络遗传算法_不想秃头的夜猫子的博客-CSDN博客https://blog.csdn.net/golden_knife/article/details/128510731通俗易懂地解释遗传算法 - 知乎 (zhihu.com)https://zhuanlan.zhihu.com/p/136393730遗传算法解决旅行商问题（详细解释+代码分享） - 知乎 (zhihu.com)https://zhuanlan.zhihu.com/p/344588977用遗传算法求解旅行商问题_中国旅行商问题,34个省会-CSDN博客https://blog.csdn.net/breeze_blows/article/details/102992997遗传算法（三）——适应度与选择_遗传算法适应度函数-CSDN博客https://blog.csdn.net/weixin_30239361/article/details/101540896

总结

这个最好适应度，最差适应度以及平均适应度的概念没完全掌握，不知道是不是这一个意思，所以在程序中注释了，大家可以根据自己的理解来添加。

遗传算法的思路是“适者生存，优胜劣汰”，模拟生物的进化，以一个初始生物群体为起点，经过竞争后，一部分个体被淘汰而无法再进入这个循环圈，而另一部分则胜出成为种群。对于算法的选择的个体，适应度高的并不一定进入种群，只是进入种群的可能性比较大；而适应度低的个体并不一定被淘汰，只是进入种群的可能性比较小，这个也是与生物进化论相挂钩的。