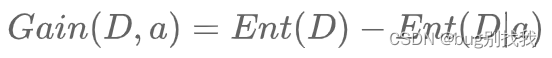坦维·佩努穆迪

一、说明
MNIST (“修改后的国家标准与技术研究所”)是事实上的计算机视觉“hello world”数据集。自 1999 年发布以来,这个经典的手写图像数据集一直作为分类算法基准测试的基础。随着新的机器学习技术的出现,MNIST 仍然是研究人员和学习者的可靠资源。
最终目标是从数万张手写图像的数据集中正确识别数字。

图片来源:维基百科
我们现在将尝试从头开始使用KNN(K 最近邻)算法对数字进行分类。
在此之前,我们先来了解一下KNN到底是什么!
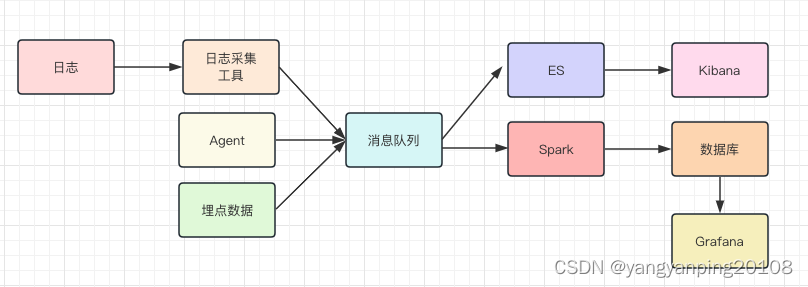
二、如何读取Mnist?
读取Mnist可以用tensorflow完成,也可以用numpy完成。如下:
def load_data(path):
with np.load(path) as f:
x_train, y_train = f['x_train'], f['y_train']
x_test, y_test = f['x_test'], f['y_test']
return (x_train, y_train), (x_test, y_test)
(x_train, y_train), (x_test, y_test) = load_data('../input/mnist-numpy/mnist.npz')三、什么是KNN?
K 最近邻可用于分类和回归。K 最近邻是一种简单的算法,它存储所有可用案例并根据相似性度量对新案例进行分类。
KNN是一种基于实例的学习或惰性学习,其中函数仅在本地进行近似,并且所有计算都推迟到分类。KNN 算法是所有机器学习算法中最简单的算法之一。
它是一种非参数算法,不需要训练数据来进行推理,因此与参数学习算法相比,训练速度要快得多,而推理速度要慢得多,原因显而易见。
四、KNN 到底是如何工作的?
我们通过一个简单的例子来理解这个算法。
以下是红色圆圈 (RC)和绿色方块 (GS)的分布:

您打算找出蓝星 (BS) 的等级。BS 可以是 RC 或 GS,仅此而已。KNN 算法中的“K”是我们希望投票的最近邻居。假设 K = 3。因此,我们现在将以 BS 为中心制作一个圆,其大小仅包含平面上的三个数据点。更多详情请参考下图:
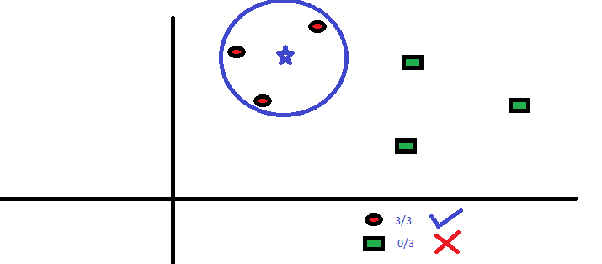
离SB最近的3个点都是RC。因此,根据我们的智能置信水平,我们可以说 bs 应该属于 RC 类别。在这里,选择变得非常明显,因为最近邻居的所有 3 票都投给了 RC。在此算法中,参数K的选择至关重要。接下来,我们将了解得出最有效的K需要考虑哪些因素。
注: KNN 的一些假设 —
- 当您有 2 个类时,请选择奇数 K 值以避免平局。即,如果新数据点位于两个类之间,则它无法决定选择哪一个。
- K 不能是类数的倍数
- 如果 K 非常小(过拟合),如果您有很多数据点 (n) 将不准确
- 如果 K 很大(Underfit),K 一定不能等于数据点的数量 n
五、我们如何选择因子K?
首先,让我们尝试了解 K 对算法到底有什么影响。如果我们看到最后一个例子,假设所有 6 个训练观察值保持不变,使用给定的 K 值,我们可以为每个类别划分边界。

正如您所看到的,训练样本在 K=1 时的错误率始终为零。这是因为与任何训练数据点最接近的点就是其本身。因此,当 K=1 时,预测总是准确的。如果验证误差曲线相似,我们选择的 K 将为 1。
以下是不同 K 值的验证误差曲线:

这让故事变得更加清晰。当 K=1 时,我们过度拟合了边界。因此,错误率最初下降并达到最小值。在最小值点之后,它会随着 K 的增加而增加。为了获得 K 的最佳值,您可以将训练和验证与初始数据集分开。现在绘制验证误差曲线以获得 K 的最佳值。这个 K 值应该用于所有预测,这与肘部方法类似。
六、KNN 的伪代码
任何人都可以按照下面给出的伪代码步骤来实现 KNN 模型。
- 加载数据
- 初始化k的值
- 要获得预测类别,请从 1 迭代到训练数据点总数
- 计算测试数据与每行训练数据之间的距离。在这里,我们将使用欧几里德距离作为距离度量,因为它是最流行的方法。其他可以使用的度量有切比雪夫、余弦等。
- 根据距离值对计算出的距离进行升序排序
- 从排序数组中获取前 k 行
- 获取这些行中最常见的类别
- 返回预测的类别
七、KNN 的变体
在传统提出的 KNN 中,正如我们所见,我们对所有类别和距离给予相同的权重,这是您应该了解的 KNN 的变体!
7.1 距离加权 KNN
在距离加权 KNN 中,您基本上更多地强调更接近测试值的值,更少地强调远离测试值的值,并类似地为每个值分配权重。

其中 wk 是 —
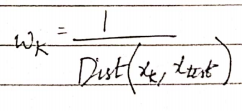
7.2 加权距离函数
由于我们在传统 KNN 中为所有特征赋予了相同的权重,因此我们尝试在此变体中为每个特征分配不同的权重。重要的特征将具有较大的权重,而不太重要的特征将具有较低的权重,而最不重要的特征将具有0或接近0的权重。

八、测量距离的方法
- 闵可夫斯基距离
- 曼哈顿距离
- 欧氏距离
- 汉明距离
- 余弦距离
当数据具有高维度时,曼哈顿距离通常优于更常见的欧几里得距离。汉明距离用于衡量分类变量之间的距离,余弦距离度量主要用于查找两个数据点之间的相似程度,明可夫斯基是欧几里德距离和曼哈顿距离在较低级别上的推广。
有关这方面的更多信息,请查看 —机器学习中使用的不同类型的距离度量。
九、从头开始实施
您最初需要导入的库:
import numpy as np
import operator
from operator import itemgetter让我们首先定义一个返回两点之间的欧几里得距离的函数:
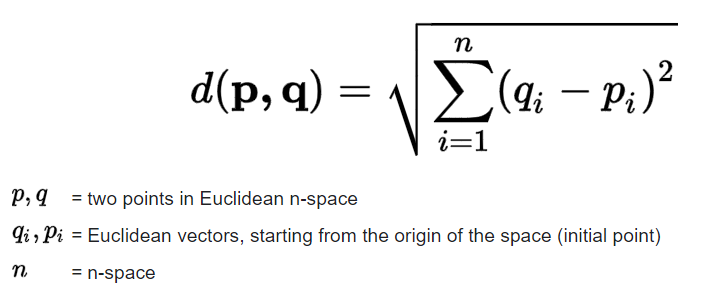
图片来源:Science Direct — 欧几里得距离公式
def euc_dist(x1, x2):
return np.sqrt(np.sum((x1-x2)**2))现在,让我们编写一个类“KNN”并为“K”值初始化一个实例:
class KNN:
def __init__(self, K=3):
self.K = K让我们在类中添加另一个函数来初始化实例以拟合我们的训练集 — X-train 和 y-train:
class KNN:
def __init__(self, K=3):
self.K = K
def fit(self, x_train, y_train):
self.X_train = x_train
self.Y_train = y_train现在让我们将预测函数添加到此类中:
def predict(self, X_test):
predictions = []
for i in range(len(X_test)):
dist = np.array([euc_dist(X_test[i], x_t) for x_t in
self.X_train])
dist_sorted = dist.argsort()[:self.K]
neigh_count = {}
for idx in dist_sorted:
if self.Y_train[idx] in neigh_count:
neigh_count[self.Y_train[idx]] += 1
else:
neigh_count[self.Y_train[idx]] = 1
sorted_neigh_count = sorted(neigh_count.items(),
key=operator.itemgetter(1), reverse=True)
predictions.append(sorted_neigh_count[0][0])
return predictions哇!这是很多代码!让我们逐行理解这一点——
我们初始化了一个列表来存储我们的预测,然后运行一个循环来计算每个测试示例到每个相应训练示例的欧几里德距离,并将所有这些距离存储在 NumPy 数组中,之后我们返回第一个 K- 的索引对距离值进行排序,然后我们创建了一个字典,其中类标签作为键,它们的出现作为每个键的值。
然后,我们将每个计数附加到每个键值对的 neigh_count 字典中,之后,我们将键值对从最常出现的值到最少出现的值进行排序,其中,我们最常出现的值将是我们对每个训练示例的预测。然后我们返回了预测。
这就是从头开始实现 KNN 的全部内容,现在让我们在 MNIST 数据集上测试我们的模型!
from sklearn.datasets import load_digits
mnist = load_digits()
print(mnist.data.shape)
Out:
(1797, 64)
X = mnist.data
y = mnist.target将我们的数据分为训练和测试:
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=123)
print(X_train.shape, y_train.shape)
print(X_test.shape, y_test.shape)
Out:
(1347, 64) (1347,)
(450, 64) (450,)
print(np.unique(y_train,return_counts=True))
print(np.unique(y_test,return_counts=True))
Out:
(array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]), array([127, 140, 136, 143, 129, 134, 133, 138, 129, 138])) (array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]), array([51, 42, 41, 40, 52, 48, 48, 41, 45, 42]))将数据分为测试和训练就足够了吗?真的有帮助吗?
通常建议使用交叉验证来分割我们的数据-
在交叉验证中,我们没有将数据拆分为两部分,而是将其拆分为 3 部分(或K取决于K 折交叉验证中的 K 值)。训练数据、交叉验证数据和测试数据。在这里,我们使用训练数据来查找最近邻居,我们使用交叉验证数据来找到“K”的最佳值(这里是 K 个邻居),最后我们在完全看不见的测试数据上测试我们的模型。这个测试数据就相当于未来未见过的数据点。
让我们导入更多辅助函数来评估 Sklearn 中的模型:
from sklearn.metrics import precision_recall_fscore_support
from sklearn.metrics import accuracy_score使用从 3 到 100 的所有可能的 K 值(奇数)训练我们的模型:
kVals = np.arange(3,100,2)
accuracies = []
for k in kVals:
model = KNN(K = k)
model.fit(X_train, y_train)
pred = model.predict(X_test)
acc = accuracy_score(y_test, pred)
accuracies.append(acc)
print("K = "+str(k)+"; Accuracy: "+str(acc))
Out:
K = 3; Accuracy: 0.9755555555555555
K = 5; Accuracy: 0.9755555555555555
K = 7; Accuracy: 0.9755555555555555
K = 9; Accuracy: 0.9755555555555555
K = 11; Accuracy: 0.9733333333333334
K = 13; Accuracy: 0.9711111111111111
K = 15; Accuracy: 0.9688888888888889
K = 17; Accuracy: 0.9666666666666667
K = 19; Accuracy: 0.9666666666666667
K = 21; Accuracy: 0.9666666666666667
K = 23; Accuracy: 0.9644444444444444
K = 25; Accuracy: 0.9644444444444444
K = 27; Accuracy: 0.9666666666666667
K = 29; Accuracy: 0.9622222222222222
K = 31; Accuracy: 0.96
K = 33; Accuracy: 0.96
K = 35; Accuracy: 0.9577777777777777
K = 37; Accuracy: 0.9577777777777777
K = 39; Accuracy: 0.9577777777777777
K = 41; Accuracy: 0.9555555555555556
K = 43; Accuracy: 0.9511111111111111
K = 45; Accuracy: 0.9488888888888889
K = 47; Accuracy: 0.9444444444444444
K = 49; Accuracy: 0.9444444444444444
K = 51; Accuracy: 0.9377777777777778
K = 53; Accuracy: 0.9355555555555556
K = 55; Accuracy: 0.9333333333333333
K = 57; Accuracy: 0.9333333333333333
K = 59; Accuracy: 0.9311111111111111
K = 61; Accuracy: 0.9333333333333333
K = 63; Accuracy: 0.9333333333333333
K = 65; Accuracy: 0.9311111111111111
K = 67; Accuracy: 0.9288888888888889
K = 69; Accuracy: 0.9266666666666666
K = 71; Accuracy: 0.9288888888888889
K = 73; Accuracy: 0.9311111111111111
K = 75; Accuracy: 0.9288888888888889
K = 77; Accuracy: 0.9266666666666666
K = 79; Accuracy: 0.92
K = 81; Accuracy: 0.9222222222222223
K = 83; Accuracy: 0.9222222222222223
K = 85; Accuracy: 0.92
K = 87; Accuracy: 0.9177777777777778
K = 89; Accuracy: 0.9177777777777778
K = 91; Accuracy: 0.9111111111111111
K = 93; Accuracy: 0.9111111111111111
K = 95; Accuracy: 0.9088888888888889
K = 97; Accuracy: 0.9088888888888889
K = 99; Accuracy: 0.9066666666666666该模型在 K=3 时最准确:
max_index = accuracies.index(max(accuracies))
print(max_index)
Out:
0绘制我们的准确性:
from matplotlib import pyplot as plt
plt.plot(kVals, accuracies)
plt.xlabel("K Value")
plt.ylabel("Accuracy")
Out:
Text(0, 0.5, 'Accuracy')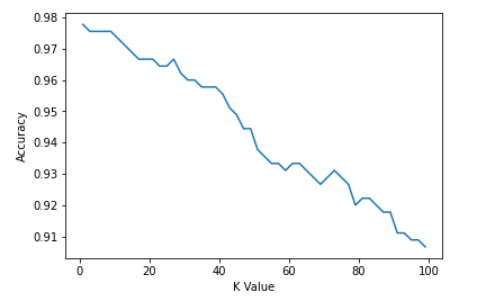
检查精确率、召回率和 F 分数(以获得最准确的 K 值):
model = KNN(K = 3)
model.fit(X_train, y_train)
pred = model.predict(X_train)
precision, recall, fscore, _ = precision_recall_fscore_support(y_train, pred)
print("Precision \n", precision)
print("\nRecall \n", recall)
print("\nF-score \n", fscore)
Out:
Precision
[1. 0.9929078 1. 1. 1. 1.
0.98518519 1. 0.9921875 0.99275362]
Recall
[1. 1. 1. 1. 1. 0.99253731
1. 0.99275362 0.98449612 0.99275362]
F-score
[1. 0.99644128 1. 1. 1. 0.99625468
0.99253731 0.99636364 0.98832685 0.99275362]在测试集上对经过训练的模型进行推理:
model = KNN(K = 3)
model.fit(X_train, y_train)
pred = model.predict(X_test)
acc = accuracy_score(y_test, pred)
precision, recall, fscore, _ = precision_recall_fscore_support(y_test, pred)
print("Precision \n", precision)
print("\nRecall \n", recall)
print("\nF-score \n", fscore)
Out:
Precision
[1. 0.89361702 1. 0.93023256 0.98113208 1.
1. 1. 1. 0.95 ]
Recall
[1. 1. 0.97560976 1. 1. 0.95833333
1. 1. 0.91111111 0.9047619 ]
F-score
[1. 0.94382022 0.98765432 0.96385542 0.99047619 0.9787234
1. 1. 0.95348837 0.92682927]
print(acc) #testing accuracy
Out:
0.9755555555555555 我知道一下子要吸收很多东西!但你坚持到了最后!对此表示敬意!不要忘记查看我即将发表的文章!