Manacher 算法，俗称马拉车算法，是一种解决最长回文子串问题的算法。

---

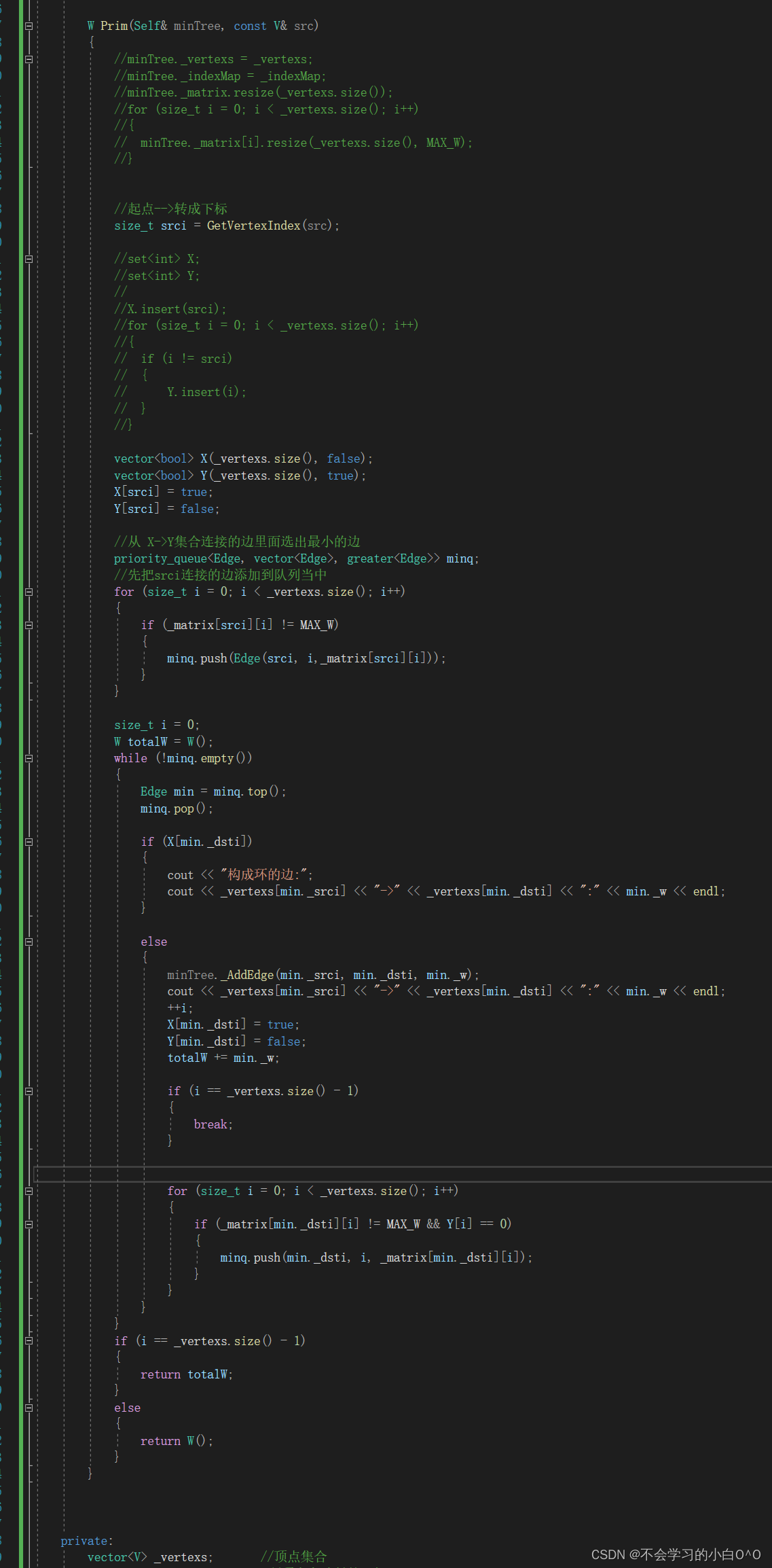
在 Ybt 的哈希章节中出现了这个：

数据范围 $10^6$，数据相对于马拉车模板较弱。

对于一个普通的字符串，我们要想求出它的回文子串需要考虑它的长度是奇数还是偶数。奇回文串的对称中心是一个，偶回文串的对称中心由两个字符共同组成。

而我们的 Manacher 算法的第一步，就是想办法让字符串的每一个回文子串都是奇回文串。我们把一个字符串的每两个字符之间插入一个相同字符（用啥都行，推荐 $），然后在开头结尾加两个不相同的字符（比如开头加一个 # 结尾加一个 @），这样就简化了后面的操作。

下面就是 Manacher 的关键部分了，敲黑板划重点！

我们假设一个数组 p[i]，它表示的是以第 $i$ 个字符为对称中心的最长回文串半径，则这个回文串实际长度为 p[i]-1（因为要扣掉 $）；定义一个 mx 表示目前找到的所有回文串中右端点最靠右的位置，这个回文串的对称中心是 mid；对于我们新找的一个位置 $i$，显然以 $i$ 为对称中心的回文子串等于以 $i$ 关于 mid 的对称点为中心的回文子串。但是我们可以发现一个问题，就是如果以 $i$ 为对称中心的这个回文串，它的右端点/左端点超出了我们当前的 mx/mx 的对称点所能覆盖的范围，那么我们无法确定在 mx 之后的情况，所以我们可以确定的 p[i] 只能等于 min(mx-i,p[mid*2-i])。接下来，我们只能暴力统计超出 mx 的部分并更新 mx 和 mid。

---

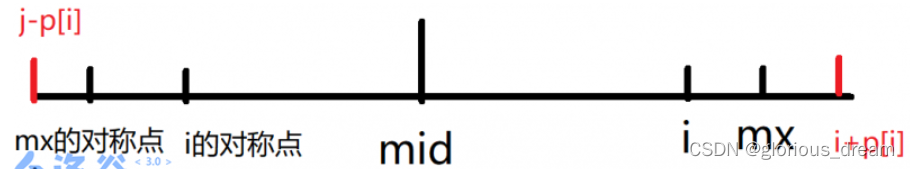
练手板子题

代码如下：

#include <bits/stdc++.h>
using namespace std;

const int maxn=4.2*1e7+5;
char s[maxn],ss[maxn];
int p[maxn];

int init()
{
	int len=strlen(ss+1);
	int j=3;
	s[1]='#',s[2]='$';
	for(int i=1;i<=len;i++)
		s[j++]=ss[i],s[j++]='$';
	s[j]='@';
	return j;
}

int manacher()
{
	int len=init(),mid=1,mx=1,ans=1;
	for(int i=1;i<=len;i++)
	{
		if(i<mx) p[i]=min(mx-i,p[mid*2-i]);
		else p[i]=1;//前面的mx一点儿用没用，直接赋为1开始暴力
		while(s[i-p[i]]==s[i+p[i]]) p[i]++;
		if(mx<i+p[i]) mid=i,mx=i+p[i];//更新mid和mx
		ans=max(ans,p[i]-1);
	}
	return ans;
}

int main()
{
	scanf("%s",ss+1);
	cout<<manacher();
	return 0;
}