1.梯度消失
考虑下图的神经网络,在使用梯度下降法迭代更新W_ki和W_ij时,它们的梯度方向间有什么关系?
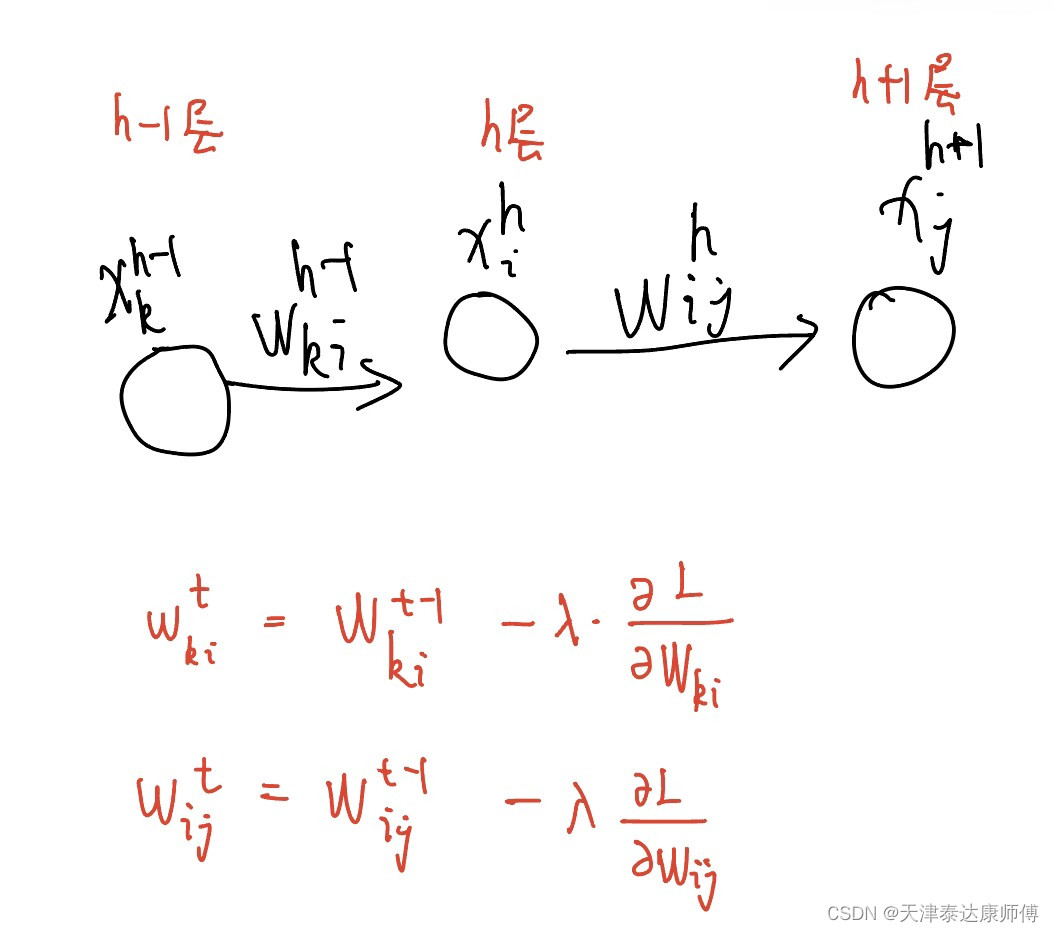
它们的梯度关系如下:
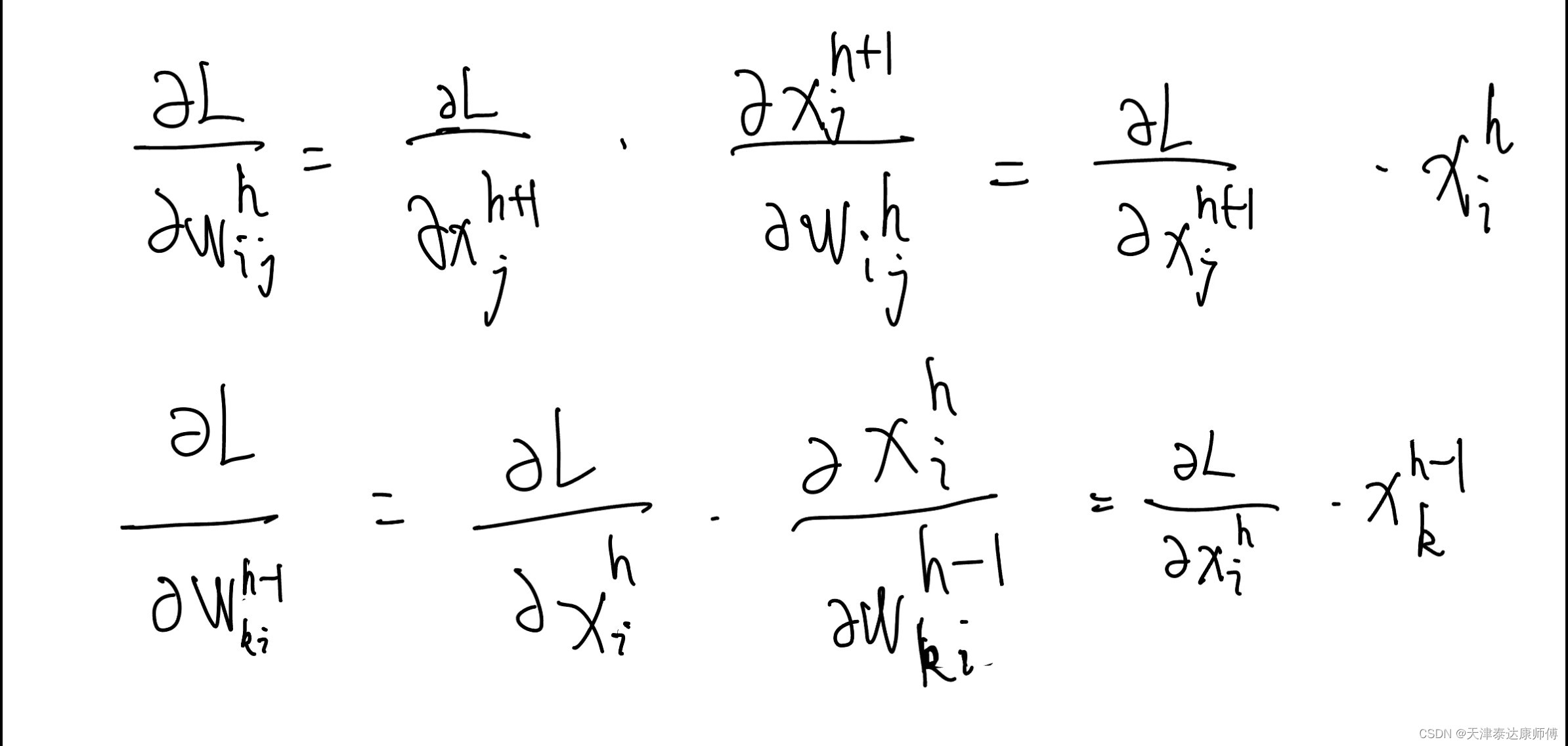
从上述两个式子我们大致可以看出,损失函数L关于第h层参数的梯度由两部分组成:1)损失函数L关于第(h+1)层特征的梯度和2)第h层特征。
进一步分析1)
L关于第(h+1)层特征的梯度和L关于第h层特征的梯度之间有什么关系?(p为第h+1层结点数)

2)第h层特征和(h-1)层特征有什么关系?
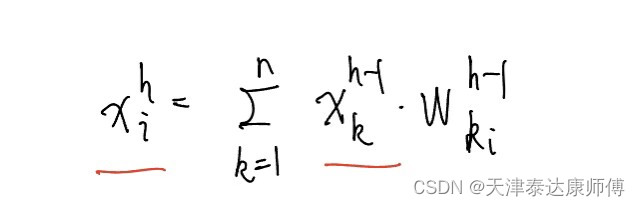
为了使得参数更新的稳定,我们应该使1)和2)的分布保持稳定,即假设相邻两层i和j,
1)Var(X_i) = Var(X_j)
2)Var(L关于X_i的偏导)=Var(L关于X_j的偏导)
X_i,X_j为两个随机变量,尽可能让它们的分布一致。
L关于X_i的偏导,L关于X_j的偏导为两个随机变量,尽可能让它们的分布也一致。这就是Xavier初始化要做的任务。经上述粗略分析,如果它们的分布不一致,就很可能造成梯度消失或梯度爆炸的情况出现。
2.Xavier初始化方法
随机变量的思想:
1.假设样本容量为n:{x1,…xn}|xi∈Rd。每个数据均为一个d维向量。假设特征和特征间独立,d个特征就对应d个相互独立的随机变量。每个特征对应一个随机变量,不同特征对应的随机变量独立。理论上来说每个特征都应对应一个与其他特征独立的正态分布。但为了简化问题,我们在数据预处理时已经对数据进行了规范化,使得每个特征独立且均满足均值为0,方差为1的正态分布。
2.假设我们只考虑一层全连接层h->h+1。h层中节点的索引用i来表示,h+1层中节点索引用j来表示。wij表示全连接网络中的参数。我们引入一个前提:h->h+1层的所有参数满足一个分布,所有参数构成了一个随机变量W,对应一个正态分布,这个随机变量W和1中所说的每个特征对应的随机变量同样相互独立。我们要确定的就是W的分布,简化考虑就是确定满足正态分布的随机变量W的均值和方差。确定了W的均值和方差,我们就可以:1)根据第h层特征的分布(均值为0,方差为1),来限制第(h+1)层特征的分布(均值为0,方差为1),2)根据L关于第(h+1)层特征的梯度(请注意,这也可以看作一个随机变量,也有对应的分布)来限制L关于第h层特征的梯度(同样也是一个随机变量)。(这也对应了Xavier初始化的两个限制条件)
接下来简单求解:
假设第h层有n个节点,第(h+1)层有p个节点。


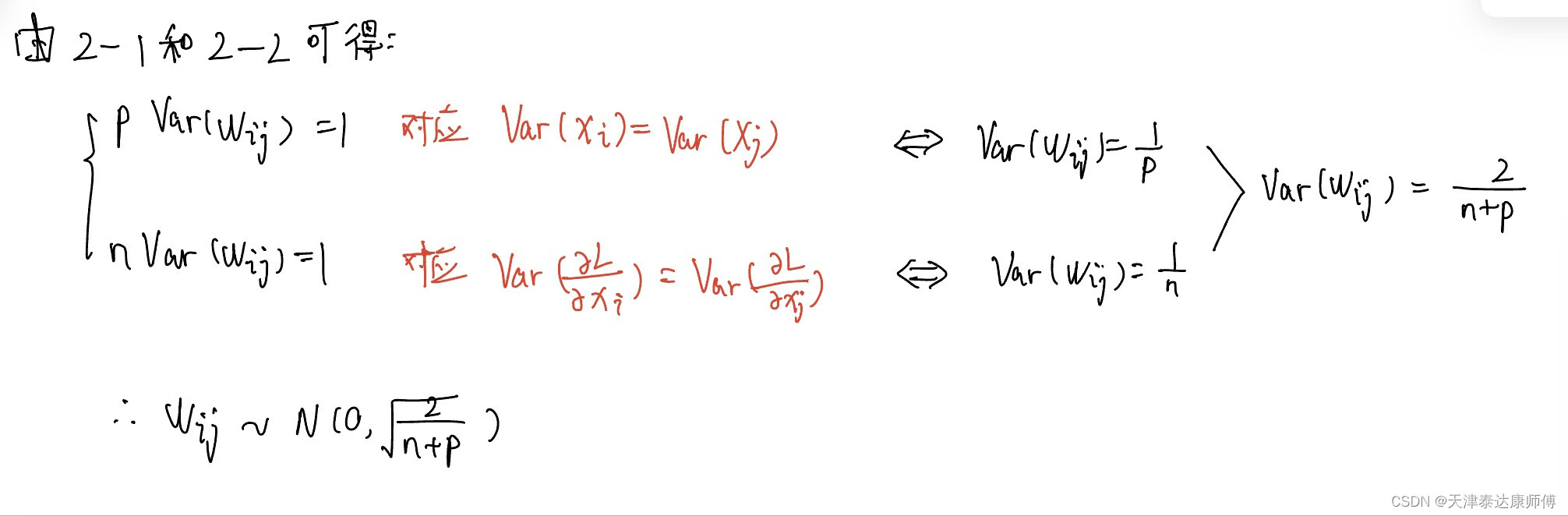
可求解W可从该正态分布中采样。
其实,我们不用管W满足什么分布,只需要保证W的均值为0,方差为2/(n+p)就可以保证各层特征的数值稳定和各层梯度的稳定,保证了这两点,就可以保证全连接网络反向传播中数值的稳定性。
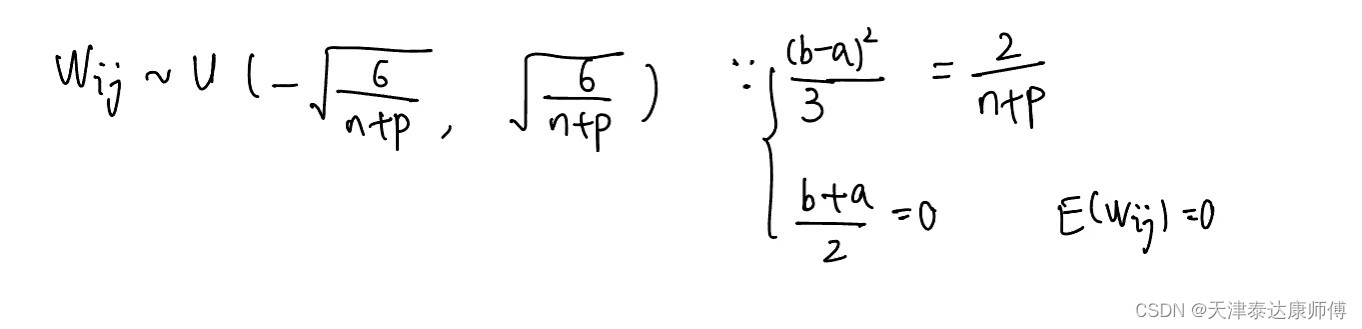
所以,W也可以满足上图所示的均匀分布U.