数据结构和算法（13）：优先级队列

概述

按照事先约定的优先级，可以始终高效查找并访问优先级最高数据项的数据结构，也统称作优先级队列

优先级队列将操作对象限定于当前的全局极值者。

根据数据对象之间相对优先级对其进行访问的方式，与此前的访问方式有着本质区别，称作 循优先级访问 (call-by-priority)。

“全局极值”本身就隐含了“所有元素可相互比较”这一性质。然而，优先级队列并不一定需要动态维护这个全序，却转而维护一个偏序（partial order）关系。
因此：优先级队列不仅足以高效地支持仅针对极值对象的接口操作，更可有效地控制整体计算成本。

词条（entry）：优先级队列中的数据项；
关键码（key）：与特定优先级相对应的数据属性；
作为确定词条优先级的依据，关键码之间必须可以比较大小.

基本实现

优先级队列作为一类独特数据结构的意义在于通过转而维护词条集的一个偏序关系。

操作接口

操作结构	功能描述
`size()`	报告优先级队列的规模，即其中词条的总数
`insert()`	将指定词条插入优先级队列
`getMax()`	返回优先级最大的词条（若优先级队列非空）
`delMax()`	删除优先级最大的词条（若优先级队列非空）

接口定义

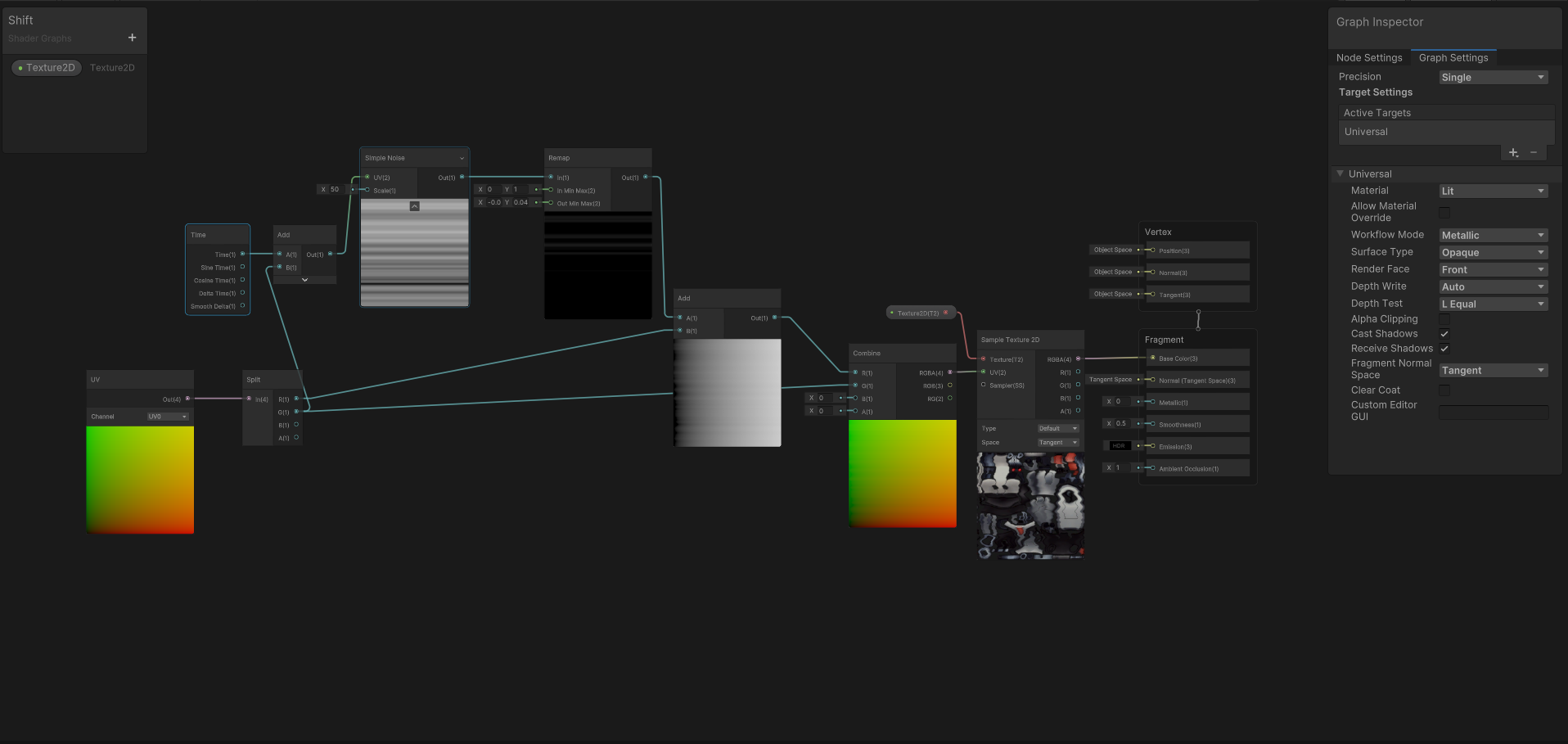
template <typename T> struct PQ { // 优先级队列 PQ 模板类
	virtual void insert ( T )= ; // 按照比较器确定的优先级次序插入词条
	virtual T getMax() = ; // 取出优先级最高的词条
	virtual T delMax() = ; // 删除优先级最高的词条
}

因为这一组基本的ADT接口可能有不同的实现方式，故这里均以虚函数形式统一描述这些接口，以便在不同的派生类中具体实现。
借助无序列表、有序列表、无序向量或有序向量，都难以同时兼顾insert()和delMax()操作的高效率。

完全二叉堆：结构

结构性： 逻辑结构须等同于完全二叉树，如此，堆节点将与词条一一对应；
堆序性： 优先级而言，堆顶以外的每个节点都不高（大）于其父节点；

堆中优先级最高的词条必然始终处于堆顶位置。因此，堆结构的getMax()操作总是可以在O(1)时间内完成。
堆顶以外的每个节点都不低（小）于其父节点。
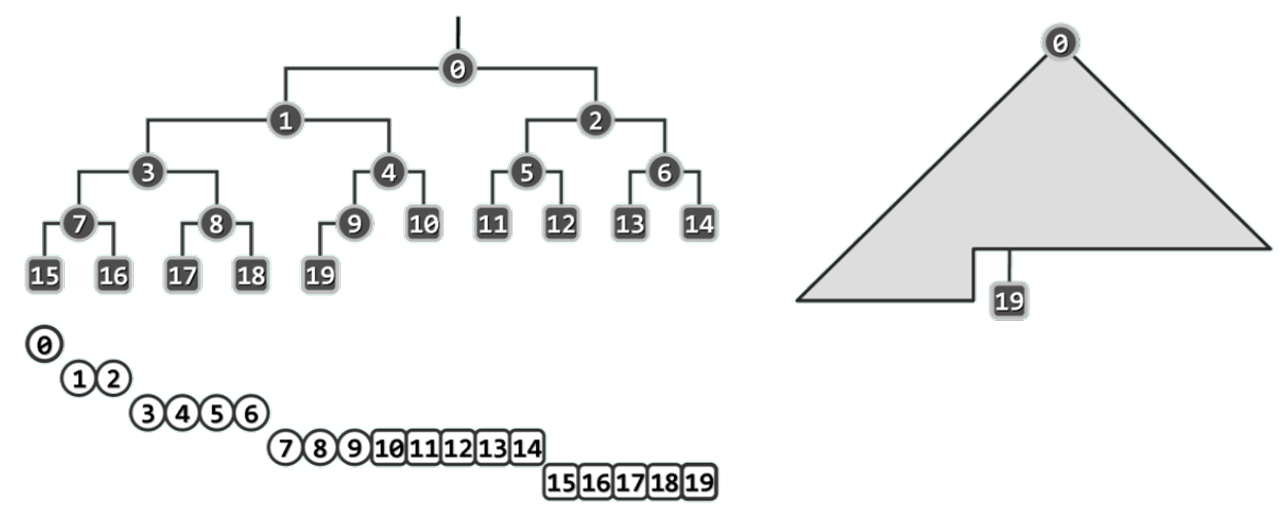
在这里插入图片描述
结构等同于完全二叉树：n 个词条组成的堆的高度 $\lfloor \log_2 n \rfloor = \cal O(logn)$ 。
insert()和delMax()操作的时间复杂度将线性正比于堆的高度h，故它们均可在O(logn)的时间内完成。

完全二叉堆的拓扑联接结构，完全由其规模n确定。节点在物理上连续排列，故总共仅需O(n)空间，而且利用各节点的编号（或秩），也可便捷地判别父子关系。

实现

#include "../Vector/Vector.h" //借助多重继承机制，基于向量
#include "../PQ/PQ.h" //按照优先级队列ADT实现的
template <typename T> class PO ComplHeap : public POT>, public Vector<T>[ //完全二又堆
protected:
	Rank percolateDown ( Rank n，Rank i ); //下滤
	Rank percolateUp ( Rank i ); //上滤
	void heapify ( Rank n ); //Floyd建堆算法
public:
	PQ_ComplHeap()[}//默认构造
	PQ_ComplHeap ( T* A, Rank n )[ copyFrom ( A,,n ); heapify ( n );} //批量构造
	void insert ( T );//按照比较器确定的优先级次序，插入词条
	T getMax();//读取优先级最高的词条
	T delMax(); //删除优先级最高的词条}; //PO CompIHeap

全局优先级最高的词条总是位于堆顶：只需返回向量的首单元，即可在O(1)时间内完成getMax()操作。

template<typename T> Y PQ_ComplHeap<T>::getMax() {return _elem[0];	//取优先级最高的词条

完全二叉堆：插入与上滤

插入算法分为两个步骤：1. 首先将新词条接至向量末尾； 2.再对该词条实施上滤调整。
在这里插入图片描述

template <typename T> void PQ_ComplHeap<T>::insert (Te){ //将词条插入完全二叉堆中
	Vector<T>::insert ( e ); //首先将新词条接至向量未尾
	percolateUp ( _size - 1 ); //再对该词条实施上滤调整
}

尽管此时如图(a)所示，新词条的引入并未破坏堆的结构性，但只要新词条e不是堆顶，就有可能与其父亲违反堆序性。所以需要对新接入的词条做适当调整，在保持结构性的前提下恢复整体的堆序性。

上滤

假定原堆非空，于是新词条e的父亲p（深色节点）必然存在。
根据e在向量中对应的秩，可以简便地确定词条p对应的秩，即 $\lceil i(e) - 1) \rceil$ 。
若经比较判定 $\leq p$ ，则堆序性在此局部以至全堆均已满足，插入操作因此即告完成。反之，若 $e > p$ ，则可在向量中令 e 和 p 互换位置。如图(b)所示，如此不仅全堆的结构性依然满足，而且e和p之间的堆序性也得以恢复。
当然，此后e与其新的父亲，可能再次违背堆序性。若果真如此，继续套用以上方法，如图( c)所示令二者交换位置。

每交换一次，新词条e都向上攀升一层，故这一过程也形象地称作上滤（percolate up）。一旦上滤完成，则如图(d)所示，全堆的堆序性必将恢复。

//对向量中的第i个词条实施上滤操作，i < _size
template <typename T> Rank PQ ComplHeap<T>::percolateUp ( Rank i ){
	while ( ParentValid ( i ) ) //只要i有父亲( 尚未抵达堆顶)，则
		Rank j = Parent (i); //将i之父记作j
		if ( lt ( _elem[i], _elem[j] ) ) break; //一旦当前父子不再逆序，上滤旋即完成s
		wap ( _elem[i], _elem[j] );i = j; //否则，父子交换位置，并继续考查上一层
	}//while
	return i; //返回上滤最终抵达的位置
}

上滤调整过程中交换操作的累计次数，不致超过全堆的高度 log2 n。而在向量中，每次交换操作只需常数时间，故上滤调整乃至整个词条插入算法整体的时间复杂度，均为 O(logn)。

实例
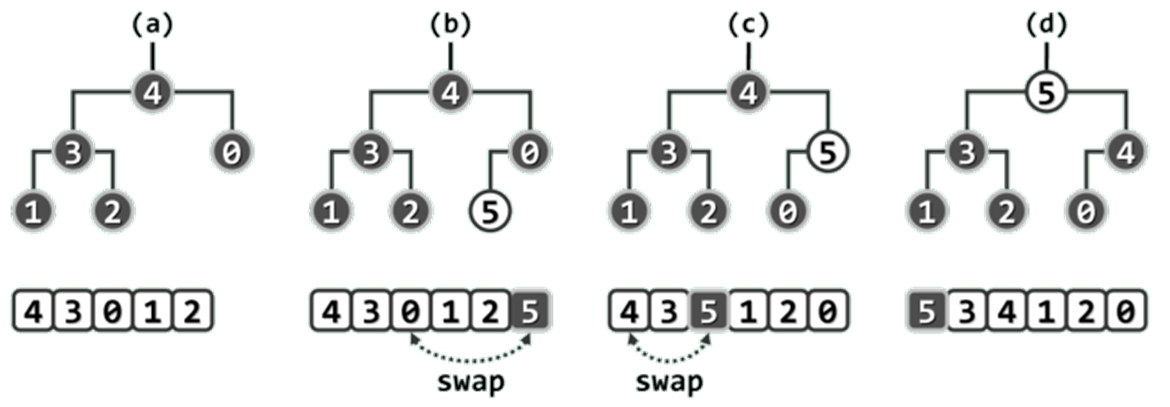
在这里插入图片描述
在如图(a)所示由5个元素组成的初始完全堆中，现拟插入关键码为5的新元素。为此，首先如图(b)所示，将该元素置于向量的末尾。此时，新元素5与其父节点0逆序，故如图©所示，经一次交换之后，新元素5上升一层。此后，新元素5与其新的父节点4依然逆序，故如图(d)所示，经一次交换后再上升一层。此时因已抵达堆顶，插入操作完毕，故算法终止。

//对向量中的第i个词条实施上滤操作，i < _size
template <typename T> Rank PQ_ComplHeap<T> :: percolateUp ( Rank i ) {
	while ( Parentvalid ( i ) ) { //只要i有父亲(尚未抵达堆顶），则
		Rank j = Parent ( i );	//将i之父记作j
		if ( lt ( _elem[i]，_elem[j] ) ) break; //一旦当前父子不再逆序，上滤旋即完成
		swap (_elem[i]，_elem[j]); i = j; //否则，父子交换位置，并继续考查上一层
	}	//while
	return i;	//返回上滤最终抵达的位置
}

完全二叉堆：删除与下滤

删除算法也分为两个步骤：1.待删除词条r总是位于堆顶，可直接将其取出并备份；2.摘除堆顶（首词条)，代之以末词条，对新堆顶实施下滤，将最末尾的词条e转移至堆顶。

template <typename T> T PQ_ComplHeap<T>::delMax() {	//删除非空完全二叉堆中优先级最高的词条
	T maxElem = _elem[0]; _elem[0] = _elem[ --_size ];	//摘除堆顶（首词条），代之以末词条
	percolateDown ( _size, 0 );	//对新堆顶实施下滤
return maxElem;	//返回此前备份的最大词条

实例
在这里插入图片描述

若新堆顶e不满足堆序性，则可如图(c )所示，将e与其(至多)两个孩子中的大者(图中深色节点）交换位置。与上滤一样，由于使用了向量来实现堆，根据词条e的秩可便捷地确定其孩子的秩。
此后，堆中可能的缺陷依然只能来自于词条e——它与新孩子可能再次违背堆序性。若果真如此，继续套用以上方法，将e与新孩子中的大者交换，结果如图(d)所示。实际上，只要有必要，此后可如图(e)和(f)不断重复这种交换操作。

因每经过一次交换，词条e都会下降一层，故这一调整过程也称作下滤（percolate down）。
下滤乃至整个删除算法的时间复杂度也为O(logn)

//对向量前 n 个词条中的第 i 个实施下滤，i < n
template <typename T> Rank PQ_ComplHeap<T> :: percolateDown ( Rank n，Rank i ) {
	Rank j; //i及其(至多两个)孩子中，堪为父者
	while ( i != ( j = ProperParent ( _elem，n, i ) ))	//只要 i 非 j，则
		{ swap ( _elem[i]，_elem[j] ); i = j; }	//二者换位，并继续考查下降后的 i
	return i;	//返回下滤抵达的位置(亦 i 亦 j)
}

完全二叉堆：批量建堆

建堆：给定一组词条，高效地将它们组织成一个堆。

蛮力算法

从空堆起反复调用标准insert()接口，即可将输入词条逐一插入其中，并最终完成建堆任务。
具体地，若共有n个词条，则共需迭代n次。第k轮迭代耗时O(logk)，故累计耗时间量应为：O(log1 + log2 + ... + logn) = O(logn!) = O(nlogn)。

自上而下的上滤：对任何一棵完全二叉树，只需自顶而下、自左向右地针对其中每个节点实施一次上滤，即可使之成为完全二叉堆。在此过程中，为将每个节点纳入堆中，所需消耗的时间量将线性正比于该节点的深度：O(nlogn)。

Floyd 算法

任给堆 $H_0$ 和 $H_1$ ，以及另一独立节点 $p$ ，如何高效地将 $H_0 \cup \{P\} \cup H_1$ 转化为堆？
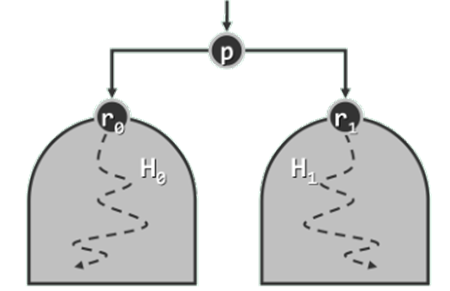
在这里插入图片描述
首先为满足结构性，可将这两个堆当作 $p$ 的左、右子树，联接成一棵完整的二叉树。此时若 $p$ 与孩子 $r_0$ 和 $r_1$ 满足堆序性，则该二叉树已经就是一个不折不扣的堆。
此时的场景完全等效于，在delMax()操作中摘除堆顶，再将末位词条 $(p)$ 转移至堆顶。
自底而上地反复套用可不断地将处于下层的堆捉对地合并成更高一层的堆，并最终得到一个完整的堆。
按照这一构思，即可实现 Floyd 建堆算法：

template <typename T> void PQ_ComplHeap<T>::heapify ( Rank n ) { //Floyd建堆算法，O(n)时间
	for ( int i = LastInternal ( n ); InHeap ( n, i ); i-- )	//自底而上，依次
		percolateDown ( n, i );	//下滤各内部节点
}

只需自下而上、由深而浅地遍历所有内部节点，并对每个内部节点分别调用一次下滤算法percolateDown()。

实例

在这里插入图片描述

复杂度
算法依然需做n步迭代，以对所有节点各做一次下滤。这里，每个节点的下滤所需的时间线性正比于其高度，故总体运行时间取决于各节点的高度总和。

不妨仍以高度为h、规模为 $n = 2^{h+1} - 1$ 的满二叉树为例做一大致估计，运行时间应为：O(n)。
由于在遍历所有词条之前，绝不可能确定堆的结构，故以上已是建堆操作的最优算法。
各节点所消耗的时间线性正比于其深度——而在完全二叉树中，深度小的节点，远远少于高度小的节点。

堆排序

堆排序算法： 对于向量中的 n 个词条，借助堆的相关算法，实现高效的排序。
将所有词条分成未排序和已排序两类，不断从前一类中取出最大者，顺序加至后一类中。算法启动之初，所有词条均属于前
一类；此后，后一类不断增长；当所有词条都已转入后一类时，即完成排序。

将其划分为前缀H和与之互补的后缀S，分别对应于上述未排序和已排序部分。
与常规选择排序算法一样，在算法启动之初H覆盖所有词条，而S为空。新算法的不同之处在于，整个排序过程中，无论H包含多少词条，始终都组织为一个堆。
H中的最大词条不会大于S中的最小词条——除非二者之一为空，比如算法的初始和终止时刻。

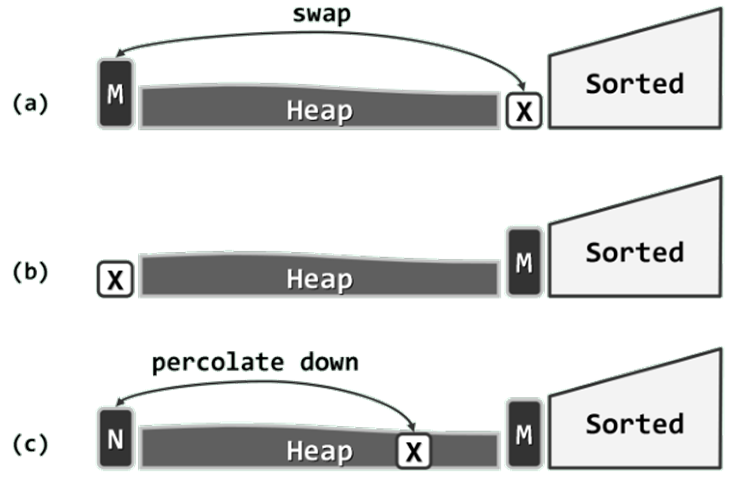
在这里插入图片描述
首先如图(a)，取出首单元词条M，将其与末单元词条x交换。M既是当前堆中的最大者，同时根据不变性也不大于S中的任何词条，故如此交换之后M必处于正确的排序位置。
如图(b)，此时可等效地认为S向前扩大了一个单元，H相应地缩小了一个单元。请注意，如此重新分界之后的H和S依然满足以上不变性。至此,唯一尚未解决的问题是，词条x通常不能“胜任”堆顶的角色。
最后如图(c )，对X实施一次下滤调整，即可使H整体的堆序性重新恢复。

复杂度
在每一步迭代中，交换M和X只需常数时间，对x的下滤调整不超过O(logn)时间。因此，全部n步迭代累计耗时不超过O(nlogn)。即便使用蛮力算法而不是Floyd算法来完成H的初始化，整个算法的运行时间也不超过O(nlogn)。

实现

template ctypename T〉 void Vector<T>::heapSort ( Rank lo，Rank hi ) { //0 <= lo < hi 〈= size
	PQ_ComplHeap<T> H ( _elem + lo , hi - lo );	//将待排序区间建成一个完全二叉堆，O(n)
	while ( !H.empty() )	//反复地摘除最大元并归入已排序的后缀，直至堆空
		_elem[--hi] = H.delMax( );	//等效于堆顶与末元素对换后下滤
}

左式堆：结构

堆合并：任给堆A和堆B，将二者所含的词条组织为一个堆。
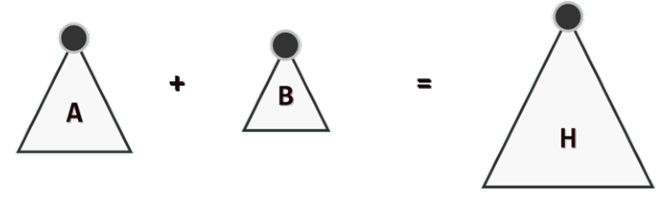
在这里插入图片描述

简单方法1：反复取出堆 B 的最大词条并插入堆 A 中；当堆 B 为空时，堆 A 即为所需的堆 H。

while ( ! B.empty() )
	A.insert( B.delMax() );

将两个堆的规模分别记作 $n$ 和 $m$ ，且 $\geq m$ 。每一步迭代均需做一次删除操作和一次插入操作，分别耗时 $\mathcal O(\log m)$ 和 $\mathcal O(\log(n + m))$ 。因共需做 $m$ 步迭代，故总体运行时间应为：
$\times [ \mathcal O( \log m) + \mathcal O(\log (n + m))] = \mathcal O(m \log(n + m)) = \mathcal O(m \log n)$

简单方法2：将两个堆中的词条视作彼此独立的对象，从而可以直接借助 Floyd 算法，将它们组织为一个新的堆 H。该方法的运行时间应为： $\mathcal O(n + m) = \mathcal O(n)$ .

左式堆（leftist heap）是优先级队列的另一实现方式，可高效地支持堆合并操作。
基本思路：在保持堆序性的前提下附加新的条件，使得在堆的合并过程中，只需调整很少量的节点。
具体地，需参与调整的节点不超过O(logn)个，故可达到极高的效率。
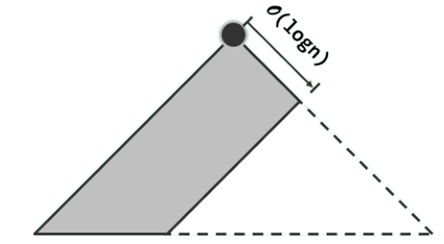
在这里插入图片描述
左式堆的整体结构呈单侧倾斜状；依照惯例，其中节点的分布均偏向左侧。也就是说，左式堆将不再如完全二叉堆那样满足结构性。

#include "../PQ/PQ.h"	//引入优先级队列ADT
#include "../BinTree/BinTree.h"	//引入二叉树节点模板类
template <typename T>
class PQ_LeftHeap : public PQ<T>, public BinTree<T>{	//基于二叉树，以左式堆形式实现的PQ
public:
	PO_LeftHeap() { }//默认构造
	Po_LeftHeap ( T* E, int n )	//批量构造:可改进为Floyd建堆算法
	{ for ( int i = 0; i < n; i++ ) insert (E[i]);	}
	void insert ( T );	//按照比较器确定的优先级次序插入元素
	T getMax();	//取出优先级最高的元素
	T delMax();	//删除优先级最高的元素
}; //Po_LeftHeap

PQ_LeftHeap首先继承了优先级队列对外的标准ADT接口。另外，既然左式堆的逻辑结构已不再等价于完全二叉树，改用紧凑性稍差、灵活性更强的二叉树结构，将更具针对性。其中蛮力式批量构造方法耗时O(nlogn)，利用Floyd算法可改进至O(n)。

空节点路径长度

节点x的空节点路径长度（null path length），记作npl(x)。若x为外部节点，则约定npl(x) = npl(null) = 0。反之若x为内部节点，则npl(x)可递归地定义为：npl(x) = 1 + min( npl(lc(x)), npl(rc(x)) )。
节点x的npl值取决于其左、右孩子npl值中的小者。
npl(x)既等于x到外部节点的最近距离，同时也等于以x为根的最大满子树的高度。

左倾性与左式堆

左式堆是处处满足“左倾性”的二叉堆，即任一内部节点x都满足： $\text{npl}(lc(x)) \geq \text{npl}(rc(x))$
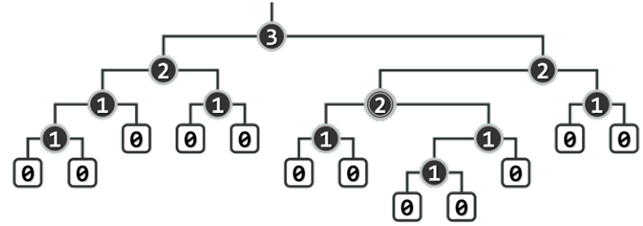
在这里插入图片描述
左式堆：左孩子的npl值不小于右孩子，而前者的高度却可能小于后者。

左式堆中任一内节点x都应满足：npl(x) = 1 + npl(rc(x))
左式堆中每个节点的npl值，仅取决于其右孩子。

最右侧通路

从x出发沿右侧分支一直前行直至空节点，经过的通路称作其最右侧通路，记作rPath(x)。
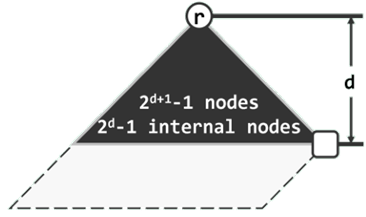
在这里插入图片描述
每个节点的npl值，应恰好等于其最右侧通路的长度。

rPath(r)的终点必为全堆中深度最小的外部节点。
若记： $n pl (r) = ∣ r P a t h (r) ∣ = d$ ，则该堆应包含一棵以 $r$ 为根、高度为 $d$ 的满二叉树（黑色部分），且该满二叉树至少应包含 $2^{d+1} -1$ 个节点、 $2^d - 1个$ 内部节点——这也是堆的规模下限。反之，在包含 $n$ 个节点的左式堆中，最右侧通路必然不会长于：log2(n+1)-1 = O(logn)。

左式堆：合并算法

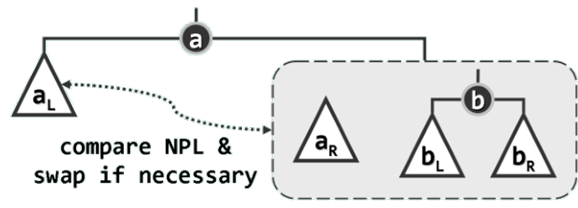
在这里插入图片描述
递归地将 $a$ 的右子堆 $a_R$ 与堆 $b$ 合并，然后作为节点 $a$ 的右孩子替换原先的 $a_R$ 。最后比较a左、右孩子的 npl 值——如有必要还需将二者交换，以保证左孩子的 npl 值不低于右孩子。

实现

template <typename T>	//根据相对优先级确定适宜的方式，合并以a和b为根节点的两个左式堆
static BinNodePosi(T) merge ( BinNodePosi(T) a，BinNodePosi(T) b ) {
	if ( ! a ) return b;//退化情况
	if ( ! b ) return a;//退化情况
	if ( lt ( a->data，b->data ) ) swap ( a, b );//一般情况∶首先确保b不大
	a->rc = merge ( a->rc, b );	//将a的右子堆，与 b 合并
	a->rc->parent = a;//并更新父子关系
	if ( !a->lc || a->lc->npl < a->rc->npl )	//若有必要
		swap ( a->lc，a->rc );	//交换a的左、右子堆，以确保右子堆的npl不大
	a->npl = a->rc ? a->rc->npl + 1 : 1;	//更新a的npl
	return a;//返回合并后的堆顶
}	//算法只实现结构上的合并

首先判断并处理待合并子堆为空的平凡情况。然后再通过一次比较，以及在必要时所做的一次交换，以保证堆顶a的优先级总是不低于另一堆顶b。
递归地将a的右子堆与堆b合并，并作为a的右子堆重新接入。递归返回之后，还需比较此时a左、右孩子的npl值，如有必要还需令其互换，以保证前者不小于后者。此后，只需在右孩子npl值的基础上加一，即可得到堆顶a的新npl值。至此，合并方告完成。

复杂度
递归只可能发生于两个待合并堆的最右侧通路上。
若待合并堆的规模分别为n和m，则其两条最右侧通路的长度分别不会超过O(logn)和O(logm)，因此合并算法总体运行时间应不超过：O(logn) + O(logm) = O( logn + logm ) = O(log(max(n, m)))

左式堆：插入和删除

基于堆合并操作实现删除接口

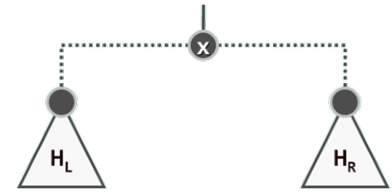
在这里插入图片描述
在摘除x之后，HL 和HR 即可被视作为两个彼此独立的待合并的堆。
于是，只要通过merge()操作将它们合并起来，则其效果完全等同于一次常规的delMax()删除操作。

template <typename T> T PQ_LeftHeap<T>::delMax(){	//基于合并操作的词条删除算法（当前队列非空)
	BinNodePosi(T) lHeap = _root->lc; 	//左子堆
	BinNodePosi(T) rHeap = _root->rc;	//右子堆
	T e = _root->data; delete _root; _size--;	//删除根节点
	_root = merge ( lHeap，rHeap );		//原左右子堆合并
	if ( _root ) _root->parent = NULL;//若堆非空，还需相应设置父子链接
	return e;//返回原根节点的数据项
}

时间成本主要消耗于对merge()的调用，总体依然不超过O(logn)。

基于堆合并操作实现词条插入算法

在这里插入图片描述
只要将x也视作（仅含单个节点的）堆，则通过调用merge()操作将该堆与堆H合并之后，其效果即完全等同于完成了一次词条插入操作。

template <typename T> void PQ_LeftHeap<T>::insert ( T e ) {	//基于合并操作的词条插入算法
	BinNodePosi(T) v = new BinNode<T> ( e ); //为e创建一个二叉树节点
	_root = merge ( _root,v );	//通过合并完成新节点的插入
	_root->parent = NULL;	//既然此时堆非空，还需相应设置父子链接
	_size++;	//更新规模
}