题目代码

from flag import flag
from Crypto.Util.number import *
import gmpy2
p = getPrime(1024)
#这行生成一个大约1024位长度的随机素数，并将其赋给变量p。
q = getPrime(1024)
#类似地，这行生成另一个大约1024位长度的随机素数，并将其赋给变量q。
n = p**3*q**2
#这行计算了RSA模数n，它是p的三次方乘以q的平方。这个模数将用于加密和解密。
print("q = ",q)
print("p = ",p)
m = bytes_to_long(flag.encode())
#这行将明文消息（flag）编码为字节并将这些字节转换为一个长整数m。这个整数是要加密的消息。
c = pow(m,65537,n)
#这行使用RSA加密算法，将明文整数m使用指数65537和模数n进行加密，得到密文c。
print("c = ",c)
 
# q =  115478867870347527660680329271012852043845868401928361076102779938370270670897498759391844282137149013845956612257534640259997979275610235395706473965973203544920469416283181677660262509481282536465796731401967694683575843183509430017972506752901270887444490905891490955975762524187534052478173966117471143713
# p =  171790960371317244087615913047696670778115765201883835525456016207966048658582417842936925149582378305610304505530997833147251832289276125084339614808085356814202236463900384335878760177630501950384919794386619363394169016560485152083893183420911295712446925318391793822371390439655160077212739260871923935217
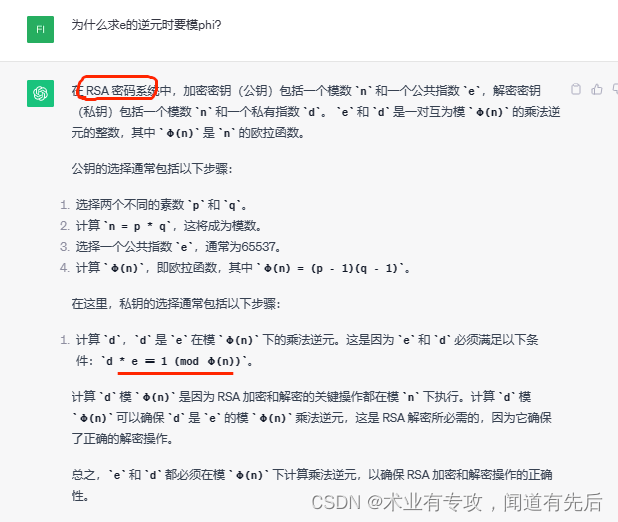
# c =  4459183928324369762397671605317600157512712503694330767938490496225669985050002776253470841193156951087663107866714426230222002399666306287642591077990897883174134404896800482234781531592939043551832049756571987010173667074168282355520711905659013076509353523088583347373358980842707686611157050425584598825151399870268083867269912139634929397957514376826145870752116583185351576051776627208882377413433140577461314504762388617595282085102271510792305560608934353515552201553674287954987323321512852114353266359364282603487098916608302944694600227628787791876600901537888110093703612414836676571562487005330299996908873589228072982641114844761980143047920770114535924959765518365614709272297666231481655857243004072049094078525569460293381479558148506346966064906164209362147313371962567040047084516510135054571080612077333228195608109065475260832580192321853906138811139036658485688320161530131239854003996457871663456850196483520239675981391047452381998620386899101820782421605287708727667663038905378115235163773867508258208867367314108701855709002634592329976912239956212490788262396106230191754680813790425433763427315230330459349320412354189010684525105318610102936715203529222491642807382215023468936755584632849348996666528981269240867612068382243822300418856599418223875522408986596925018975565057696218423036459144392625166761522424721268971676010427096379610266649911939139451989246194525553533699831110568146220347603627745407449761792135898110139743498767543521297525802809254842518002190381508964357001211353997061417710783337

很容易知道这道题考察的是欧拉函数。所以解密脚本如下：

from Crypto.Util.number import *
import gmpy2

q =  115478867870347527660680329271012852043845868401928361076102779938370270670897498759391844282137149013845956612257534640259997979275610235395706473965973203544920469416283181677660262509481282536465796731401967694683575843183509430017972506752901270887444490905891490955975762524187534052478173966117471143713
p =  171790960371317244087615913047696670778115765201883835525456016207966048658582417842936925149582378305610304505530997833147251832289276125084339614808085356814202236463900384335878760177630501950384919794386619363394169016560485152083893183420911295712446925318391793822371390439655160077212739260871923935217
#这两行分别打印出变量 q 和 p 的值，它们是RSA密钥中的两个素数因子。
c =  4459183928324369762397671605317600157512712503694330767938490496225669985050002776253470841193156951087663107866714426230222002399666306287642591077990897883174134404896800482234781531592939043551832049756571987010173667074168282355520711905659013076509353523088583347373358980842707686611157050425584598825151399870268083867269912139634929397957514376826145870752116583185351576051776627208882377413433140577461314504762388617595282085102271510792305560608934353515552201553674287954987323321512852114353266359364282603487098916608302944694600227628787791876600901537888110093703612414836676571562487005330299996908873589228072982641114844761980143047920770114535924959765518365614709272297666231481655857243004072049094078525569460293381479558148506346966064906164209362147313371962567040047084516510135054571080612077333228195608109065475260832580192321853906138811139036658485688320161530131239854003996457871663456850196483520239675981391047452381998620386899101820782421605287708727667663038905378115235163773867508258208867367314108701855709002634592329976912239956212490788262396106230191754680813790425433763427315230330459349320412354189010684525105318610102936715203529222491642807382215023468936755584632849348996666528981269240867612068382243822300418856599418223875522408986596925018975565057696218423036459144392625166761522424721268971676010427096379610266649911939139451989246194525553533699831110568146220347603627745407449761792135898110139743498767543521297525802809254842518002190381508964357001211353997061417710783337
#这行打印出变量 c 的值，它是密文。
n = p**3*q**2
#计算RSA模数 n 的值，它是 p^3 * q^2。
e = 65537
#设置公共指数 e 为65537，这是RSA公钥中的一部分
phi = (p**3-p**2)*(q**2-q)
#计算欧拉函数 phi 的值，它是 (p^3 - p^2) * (q^2 - q)。欧拉函数在RSA密钥生成和解密中非常重要。
d = gmpy2.invert(e,phi)
#使用模逆运算，计算私钥指数 d，使得 e * d ≡ 1 (mod phi)。
m = pow(c,d,n)
#使用RSA解密算法，将密文 c 使用指数 d 和模数 n 进行解密，得到明文整数 m。
# =============================================================================
# 函数是计算 x 的 y 次方，如果 z 在存在，则再对结果进行取模，其结果等效于 pow(x,y) %z。
# =============================================================================
print(long_to_bytes(m))
#print(long_to_bytes(m))：这行将明文整数 m 转换回字节形式，并将其打印出来。这是明文消息。

 flag{bu_zhi_yige_p1dsaf}

下面是出现的问题：

1. 

 

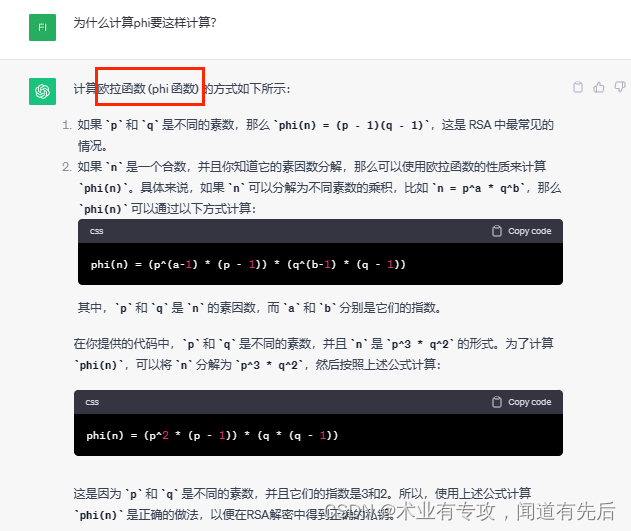
2.