定理内容:任意二端口直流网络都可以被一个等效电路替换,这个等效电路只包含一个电压源和一个串联电阻,如图1所示。
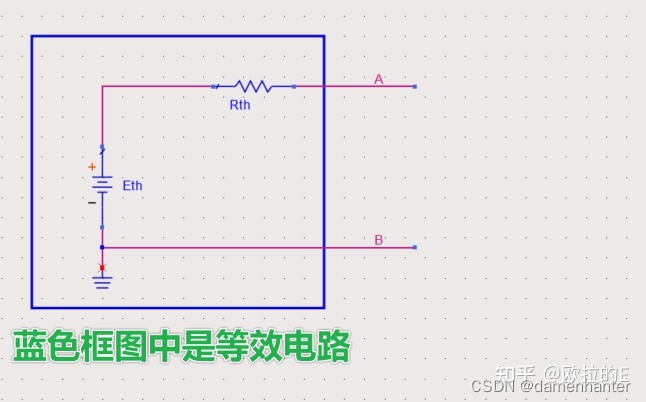
图1
戴维南定理的作用
1、分析含有非串联或非并联电源的网络
2、用最少数量的元件实现复杂网络的端口特性(端口前面的东西等效为黑匣子,只关注它对外的特性)
3、研究特定元件的变化对网络行为的影响,不需要在每次变化后分析整个网络
为了说明该定理的强大作用,考虑图2a所示的复杂网络。 定理表明整个红框区域的网络可以由一个电压源和一个电阻来替换, 如图2b所示。 如果进行正确替换, 那么这两个网络中电阻RL两端的电压及流过RL的电流将会是一样的, 并且RL的值可以任意改变。
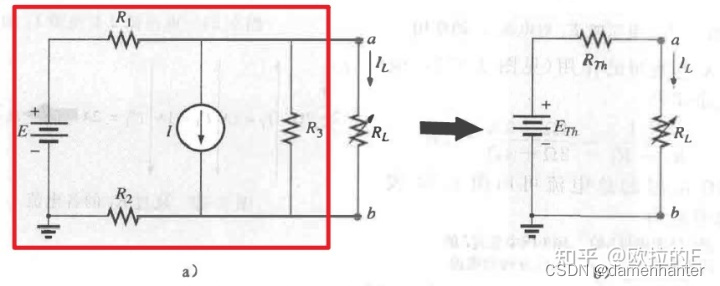
图2
戴维南等效变换步骤
1、划分出需要计算戴维南等效电路那部分网络, 将其余部分移去,并标记剩余部分的端口;
2、将所有独立源均置零,电压源用短路替代,电流源用断路替代;
3、计算等效电阻Rth,两个标记端子之间的总电阻就是Rth。如果电压源或者电流源的内阻包含在原来的网络中,那么当电源置零时要保留电源的内阻;
4、计算Eth,计算Eth时将所有电源都恢复到原来的样子,计算出2个带标记端子处的开路电压;
5、整理电路结构,将等效的电路放回到标记的2个端子上;
我们以下面的例子来说明操作步骤,原电路如图3:
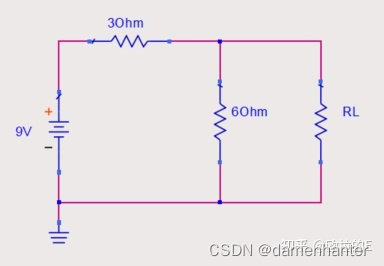
图3戴维南等效前的电路
步骤1&2:划分出需要计算戴维南等效电路那部分网络, 将其余部分移去,并标记剩余部分的端口;将所有独立源均置零,电压源用短路替代,电流源用断路替代;如图4所示:
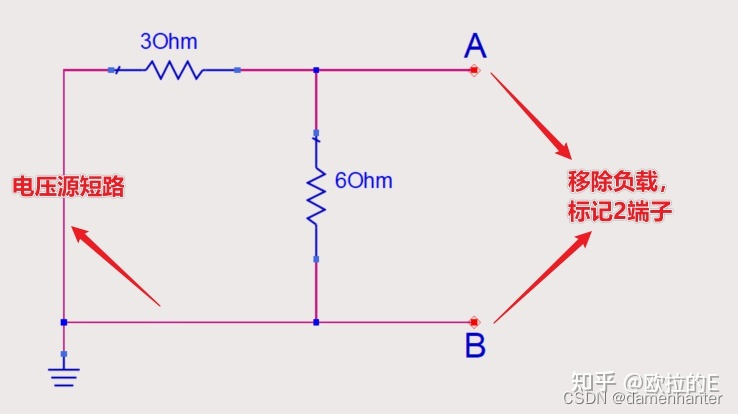
图4 处理电源和负载
步骤3:计算Rth, 由于2个电阻并联(此电路中没有电源内阻),则可得Rth=3Ohm//6Ohm=2Ohm;
步骤4:计算Eth,将所有电源都恢复到原来的样子,计算出2个带标记端子处的开路电压,Eth=9*{6/(3+6)}=6V如图5所示;
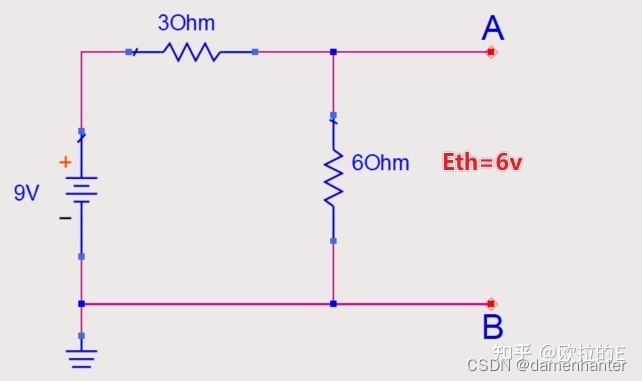
图5计算等效电压
步骤5:整理电路结构图,将等效的电路放回到标记的2个端子上,如图6所示;
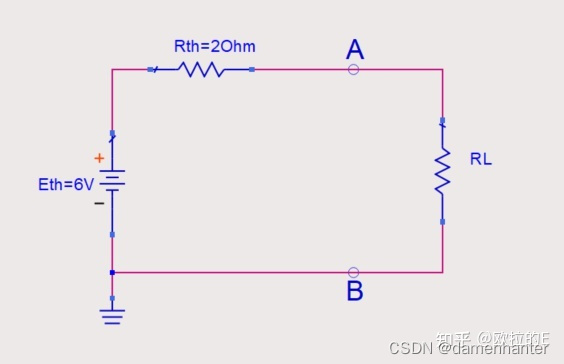
图6 戴维南等效后的电路图