v-model表单数据双向绑定-表单提交示例

news2024/10/6 18:34:56

示例如下：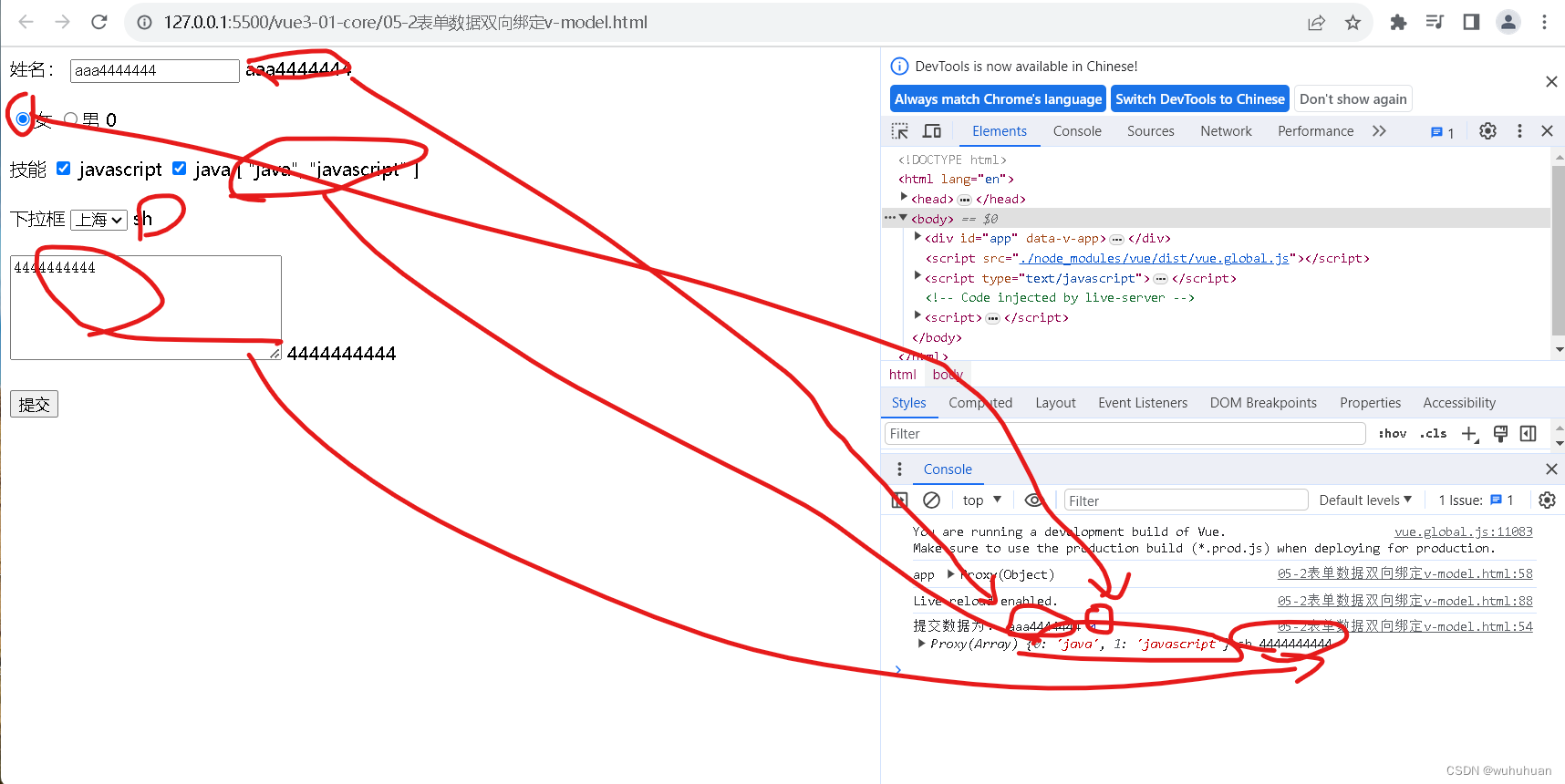

<!DOCTYPE html>
<html lang="en">
<head>
    <meta charset="UTF-8">
    <meta name="viewport" content="width=device-width, initial-scale=1.0">
    <title>v-model表单数据双向绑定</title>
</head>
<body>
    <div id="app">
        <!--@submit.prevent阻止默认的表单提交行为-->
        <form action="#" @submit.prevent="subForm">
            姓名：
            <input v-model="name" name="name" type="text">
            {{name}}
            <br><br>
            <input v-model="sex" name="sex" type="radio" :value="0">女
            <input v-model="sex" name="sex" type="radio" :value="1">男
            {{sex}}
            <br><br>
            技能
            <input v-model="skill" name="skill" type="checkbox" value="javascript"> javascript
            <input v-model="skill" name="skill" type="checkbox" value="java"> java
            {{skill}}
            <br><br>
            下拉框
            <select name="citys" v-model="citys">
                <option value="bj">北京</option>
                <option value="sh">上海</option>
                <option value="sz">深圳</option>
            </select>
            {{citys}}
            <br><br>
            <textarea v-model="remark" name="remark" cols="30" rows="6"></textarea>
            {{remark}}
            <br><br>
            <button type="submit">提交</button>
        </form>
    </div>
    <script src="./node_modules/vue/dist/vue.global.js"></script>
    <script type="text/javascript">
        const {createApp} = Vue;
        const app=createApp({
            data(){
                return{
                    name:"aaa",
                    sex: 0, //默认选中男
                    skill: ['java'], //默认勾选java
                    citys: 'sh',//默认选中
                    remark: '',//初始化textarea
                }
            },
            methods:{
                subForm(){
                    console.log("提交数据为：",this.name,this.sex,this.skill,this.citys,this.remark)
                }
            }
        }).mount("#app");
        console.log("app",app);
    </script>
</body>
</html>

ps: v-model 绑定一般为 name属性。name 属性可以删除

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1106716.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！