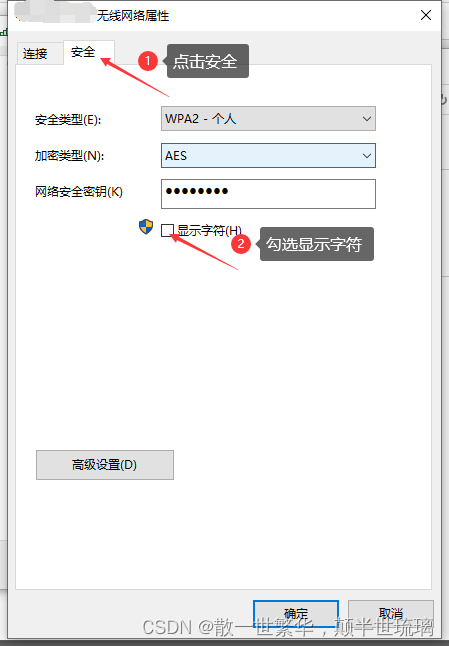
要尝试让自己安静下来,去做该做的事
而不是让内心烦躁,焦虑,毁掉你本就不多的热情和定力

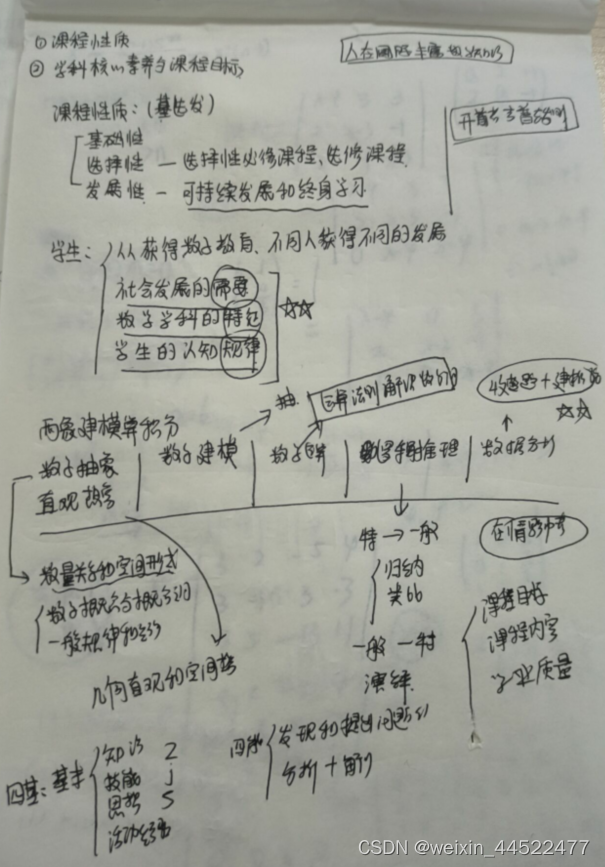



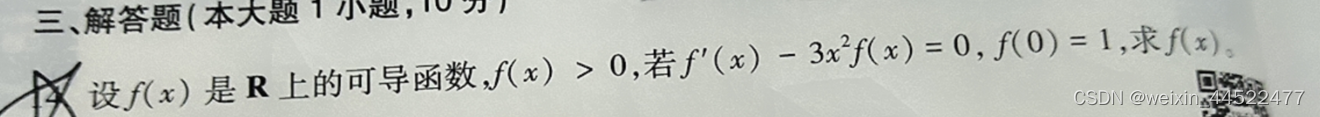
复习
import torch
import torch.nn as nn
import math
from torch.autograd import Variable
# 定义embedding类来实现文本嵌入层,这里的s说明代表两个一模一样的嵌入层,他们共享参数
class Embeddings(nn.Module):
# 类的初始化,有两个参数,d_model:指词嵌入的维度,vocab:指词表的大小
# 如果嵌入的是英文文本,vocab是英文文本的大小,如果是目标文本就是法文文本的大小
def __init__(self,d_model,vocab):
# 接着就是使用super的方式指明继承nn.Module的初始化函数
super(Embeddings, self).__init__()
# 调用nn中于定义层embdding, 获得一个词嵌入对象self.lut
# 两个参数是词表的总词数和词表的维度
# 定义embedding层
# 这两个参数位置不能写错了
self.lut = nn.Embedding(vocab,d_model)
# 最后将d_model传入类中
self.d_model = d_model
# 可以将其理解为该层的前向传播逻辑,所有层都会有此函数
# 参数x,因为embedding层是首层,所以代表输入给模型的文本通过词汇映射后的张量
# 只有一个嵌入层,所以直接扔到这里面,就可以
# 乘以是一个缩放的作用,映射的作用
def forward(self,x):
# 将x传给self.lut并与根号下self.d_model相乘作为结果返回
# x代表输入的文本通过词汇映射后的数字张量
# x代表输入进模型的文本通过词汇映射后的数字张量
return self.lut(x) * math.sqrt(self.d_model)
# # nn.Embedding演示
# # 一个参数是单词的总数,一个是嵌入的维度
# 这个10应该是最大的单词总数
# embedding = nn.Embedding(10,3)
# # 输入张量的形状是两行四列
# 进行封装
# input = torch.LongTensor([[1,2,4,5],[4,3,2,9]])
# print(embedding(input))
# # 输出的结果代表了4行3列,3这个维度展示在列这个方向,第一行共同代表了1
# # 每一个数字都被映射成为了3维的列表
#
# #
# embedding = nn.Embedding(10,3,padding_idx=0)
# input = torch.LongTensor([0,2,0,5])
# print(embedding(input))
# # 第一个和第三个都被映射成为了0
#
# embedding = nn.Embedding(10,3,padding_idx=5)
# input = torch.LongTensor([0,2,0,5])
# print(embedding(input))
# 实例化参数
# 词嵌入维度是512维
# d_model = 512
# # 词表的大小是1000
# vocab = 1000
#
# # 输入参数
# # 输入x是一个使用variable封装的长整型张量,形状是2*4
# x = Variable(torch.LongTensor([[100,2,421,508],[491,998,1,221]]))
#
# # 实例化一个emb
# 有了x 就可以实例化对象
# emb = Embeddings(d_model,vocab)
# # 将x传入到里面
# embr = emb(x)
# print("embr:",embr)
# print(embr.shape)
# 输出2*4*512
# 100 被映射为一个列表,512

高中数学课程是培养公民素质的基础性课程,简述“基础性”的含义,并举例说明:
(1)课程包括必修课程,选择性必修课程,选修课程,必修课程为学生发展提供共同基础,是高中毕业的数学学业水平考试的内容要求,也是高考的内容要求。选择性必修课程是供学生选择的的课程,也是高考的内容要求,考虑到大家有不同的选择。选修课程以学生确定发展方向为导向,为学生展示数学才能提供平台,为学生发展兴趣提供选择。
(2)面向全体学生提供了学生现阶段学习和未来发展必要的数学基础,为全体学生构建课程基础。
(3)高中数学是为了适应未来社会生活,高等教育和职业发展提供的必要的数学基础。
(4)为其他学科提供了基础。
简述“选择性”的含义
课程包括必修课程,选择性必修课程,选修课程。选择性必修课程是供学生选择的的课程,也是高考的内容要求,考虑到大家有不同的选择。选修课程以学生确定发展方向为导向,为学生展示数学才能提供平台,为学生发展兴趣提供选择。
简述发展性的含义
我们培养学生,不是为了一个高考,我们是为了培养学生全面发展,可持续发展,终身学习。
我们要发展他们的各种知识,培养数学迁移、运算能力。
为学生终身学习和可持续发展创造条件。
数学是一个怎么样的科学
数量关系和空间形式
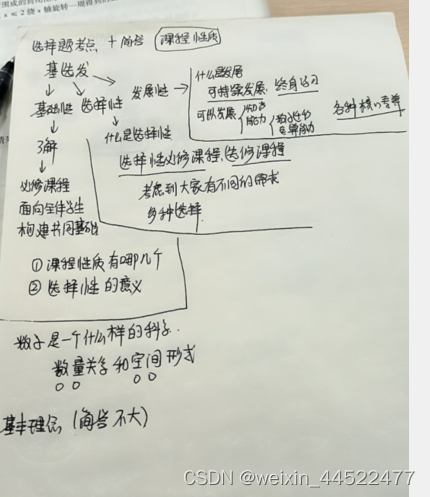
影响数学课程的因素有哪些?(数学课程内容选择的依据是什么?)
社会发展的需要
①数学与生活以及其他学科的联系
数学和生活发展越来越紧密了,我们需要在生活中运用到了数学
②提升学生应用数学解决实际问题的能力
我们应该要提升数学解决实际问题的能力
③注重数学文化的渗透
注重数学文化的渗透
处理好数学学科核心素养与知识技能之间的关系
数学学科的特征
①突出数学主线,凸显数学的内在逻辑和思想方法
②为学生发展提供共同基础和多样化选择
③处理好数学学科核心素养与知识技能之间的关系
学生的认知规律
要符合学生的认知规律
两象建模算‘积’分
数学抽象
含义:
数量关系和空间形式的抽象
内容:从数量和数量关系,图形和图形关系中抽象出数学概念及概念之间的关系
从事物的具体背景中抽象出一种规律和结构
表现:
概念规则
命题模型
方法思想
结构体系
并没有应用解决
例子:函数单调性概念中的教学中,结合实例,经历从具体的直观描述到形式的符号表达的抽象过程,加深对函数单调性概念的理解,体会用符号表达数学定义的必要性。
选择题考点
数学抽象是基本思想
逻辑推理
2021 上-选择+2017上论述
含义:从事实和命题出发,推理其他命题的素养
特殊到一般:归纳,类比
一般到特殊:演绎
合情推理:归纳推理(特殊到一般)、类比推理(特殊到特殊),椭圆推导圆
演绎推理:(一般到特殊)
表现:推理基本形式,发现问题和提出命题
举例:解决举例问题的时候,利用构建空间直角坐标系,空间向量的举例公式求解实际问题
给出一系列数据,根据数据的观察,通过分析比较,进行归纳猜想求出通项公式的过程
带动作的题
例子:构建空间直角坐标系
通项公式
非齐次线性方程组有解的充要条件是系数矩阵的秩等于增广矩阵的秩

数学建模
在现实生活当中,用数学语言,数学方法构建模型解决问题的素养




直观想象
含义:几何直观+空间想象
几何直观和空间想象
空间形式认识事物的位置关系,形态变化和运动规律
利用图形描述、分析数学问题
建立形与数的联系,构建数学问题的直观模型,探索解决问题的新思路
数学运算
数学运算能力
理解运算对象,掌握运算法则,探究运算思路,选择运算方法,设计运算程序,求得运算结果。
10.26 英语

四基+四能

课程为什么要这么设计,理念有哪些
课程理念:
人、教师、活动、评价(过程评价)
人人都获得良好的数学教育,不同的人在数学上得到不同的发展
课程方案:借鉴国际经验,体现课程改革成果,调整课程结构,改进学业知量评价
课程性质:为全体学生提供共同基础,为满足学生的不同兴趣和发展提供丰富多样的课程
课程特点:关注数学逻辑体系,内容主线、知识之间的关联,重视数学实践和数学文化