一、引言
三维曲面在实际应用中被广泛使用,能够更好的展示三维空间中曲面,以实现三维数据的可视化。
Matlab软件中可以使用mesh、fmesh、surf和fsurf等函数来实现三维曲面的绘图。其中mesh和fmesh用来绘制三维网格曲面图,surf和fsurf绘制三维曲面图。本文仅仅给出上述函数的基本用法,事实上还可以通过增加图元属性等绘制视觉效果更好的图形。
说明:下文中均是针对如下数学函数进行绘图,因此在下文中不再重述。
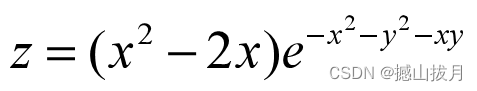
二、mesh基本用法
1)mesh
基本语法:mesh(X,Y,Z,C)
其中X、Y、Z是同维数的矩阵,分别表示空间曲面上点的横坐标矩阵、纵坐标矩阵和竖坐标矩阵。C为颜色矩阵,与Z的维数相同。
功能是绘制(X,Y,Z)生成的三维曲面的网格线图。
Demo1 :绘制三维网格图
绘制步骤:
1)指定横坐标和纵坐标的范围
2)利用函数meshgrid生成横坐标、纵坐标矩阵
3)根据已知函数生成竖坐标矩阵
4)利用函数mesh绘制网格图
%示例代码
[x,y]=meshgrid(-4:0.1:4,-3:0.1:3);
z=(x.^2-2*x).*exp(-x.^2-y.^2-x.*y);
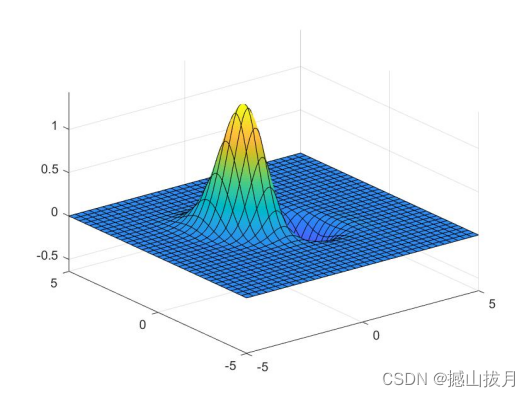
mesh(x,y,z)
%运行结果
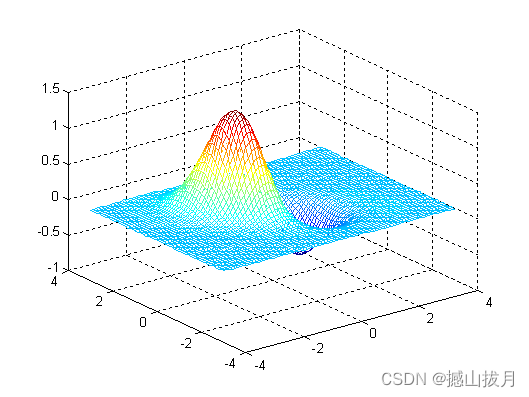
也可以在mesh中增加线条属性,其语法为:
mesh( X,Y,Z, 'PropertyName',PropertyValue,...)
%示例代码
[x,y]=meshgrid(-4:0.1:4,-3:0.1:3);
z=(x.^2-2*x).*exp(-x.^2-y.^2-x.*y);
mesh(x,y,z, 'LineWidth', 1.5 )
%运行结果
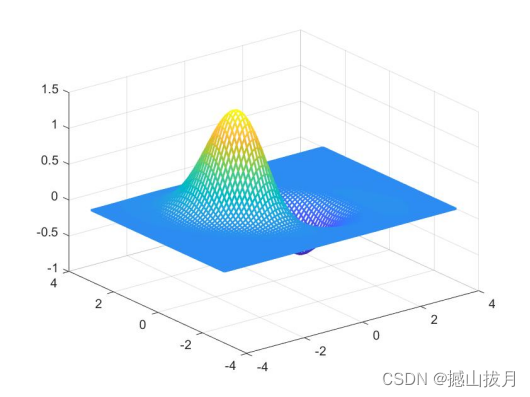
2)meshc
基本语法:meshc(X,Y,Z,C)
其中X、Y、Z是同维数的矩阵,分别表示空间曲面上点的横坐标矩阵、纵坐标矩阵和竖坐标矩阵。C为颜色矩阵,与Z的维数相同。
功能是绘制(X,Y,Z)生成的具有基本等高线的网格图。
Demo :绘制函数的三维网格图
绘制步骤:
1)指定横坐标和纵坐标的范围
2)利用函数meshgrid生成横坐标、纵坐标矩阵
3)根据已知函数生成竖坐标矩阵
4)利用函数meshc绘制网格图
%示例代码
[x,y]=meshgrid(-4:0.1:4,-3:0.1:3);
z=(x.^2-2*x).*exp(-x.^2-y.^2-x.*y);
meshc(x,y,z)
%运行结果
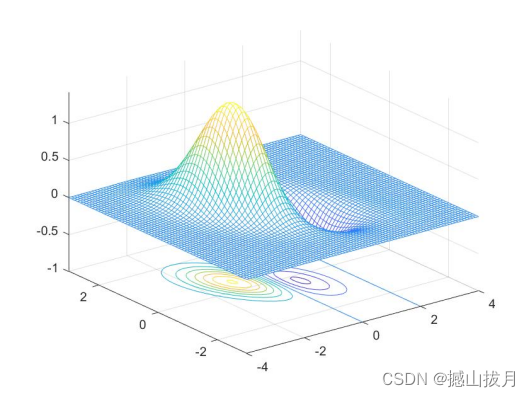
3)meshz
基本语法:meshc(X,Y,Z,C)
其中X、Y、Z是同维数的矩阵,分别表示空间曲面上点的横坐标矩阵、纵坐标矩阵和竖坐标矩阵。C为颜色矩阵,与Z的维数相同。
功能是绘制(X,Y,Z)生成的带有基准平面的网格图。
Demo :绘制带有基准平面的三维网格图
绘制步骤:
1)指定横坐标和纵坐标的范围
2)利用函数meshgrid生成横坐标、纵坐标矩阵
3)根据已知函数生成竖坐标矩阵
4)利用函数meshz绘制网格图
%示例代码
[x,y]=meshgrid(-4:0.1:4,-3:0.1:3);
z=(x.^2-2*x).*exp(-x.^2-y.^2-x.*y);
meshz(x,y,z)
%运行结果
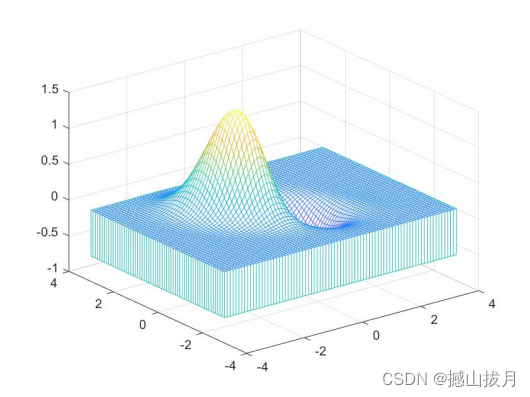
三、fmesh的基本用法
fmesh的功能是绘制二元函数fun的三维网格图,常见有下面的用法:
fmesh( fun ),横坐标和纵坐标的范围均是[-5,5]
fmesh( fun, xyinterval ),指定x和y的范围
fmesh(funx,funy,funz),参数方程形式的函数
fmesh(funx,funy,funz,uvinterval),参数方程形式的函数,并指定了参数的取值范围
Demo :绘制三维网格图
%示例代码:
fun = @(x,y)(x.^2-2*x).*exp(-x.^2-y.^2-x.*y);
fmesh(fun)
%运行结果
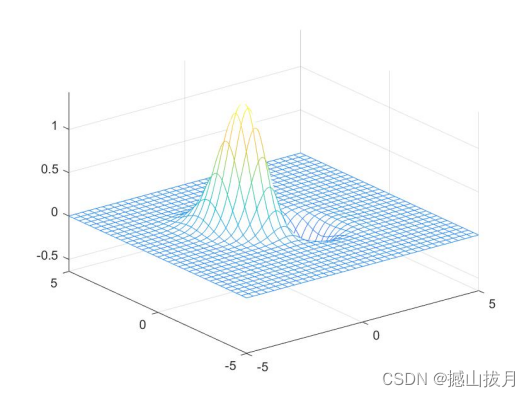
四、surf基本用法
1)surf
基本语法:surf(X,Y,Z,C)
其中X、Y、Z是同维数的矩阵,分别表示空间曲面上点的横坐标矩阵、纵坐标矩阵和竖坐标矩阵。C为颜色矩阵,与Z的维数相同。
功能是绘制(X,Y,Z)生成的三维曲面图。
注意:mesh绘图结果是网格线构成的三维曲面,而surf绘图结果是曲面片拼接而成的曲面。
Demo :绘制三维曲面
绘制步骤:
1)指定横坐标和纵坐标的范围
2)利用函数meshgrid生成横坐标、纵坐标矩阵
3)根据已知函数生成竖坐标矩阵
4)利用函数surf绘制曲面图
[x,y]=meshgrid(-4:0.1:4,-3:0.1:3);
z=(x.^2-2*x).*exp(-x.^2-y.^2-x.*y);
surf(x,y,z)
%运行结果
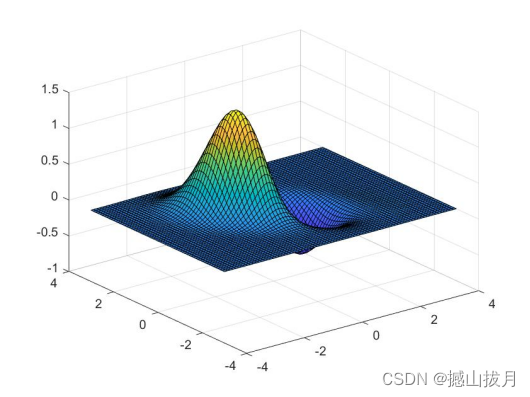
如果想得到视觉效果更好的曲面,可以增加语句shading flat以去掉曲面上的网格线
完整的代码为:
[x,y]=meshgrid(-4:0.1:4,-3:0.1:3);
z=(x.^2-2*x).*exp(-x.^2-y.^2-x.*y);
surf(x,y,z)
shading flat
可以得到如下运行结果
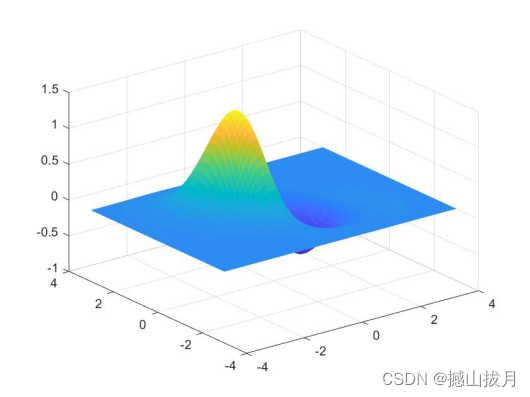
此外还可以增加语句shading interp以实现曲面颜色均匀过渡。
完整的代码为:
[x,y]=meshgrid(-4:0.1:4,-3:0.1:3);
z=(x.^2-2*x).*exp(-x.^2-y.^2-x.*y);
surf(x,y,z)
shading flat
shading interp
cmap = colorbar
可以得到如下运行结果
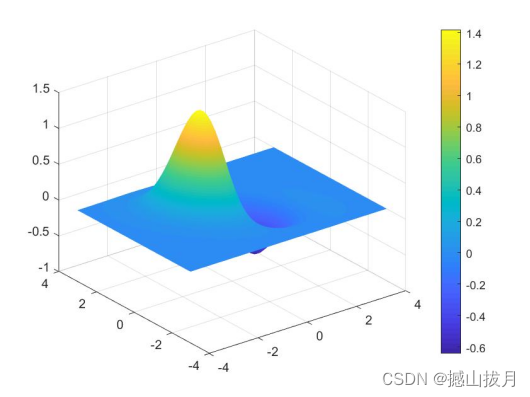
2)surfc
基本语法:surfc(X,Y,Z,C)
其中X、Y、Z是同维数的矩阵,分别表示空间曲面上点的横坐标矩阵、纵坐标矩阵和竖坐标矩阵。C为颜色矩阵,与Z的维数相同。
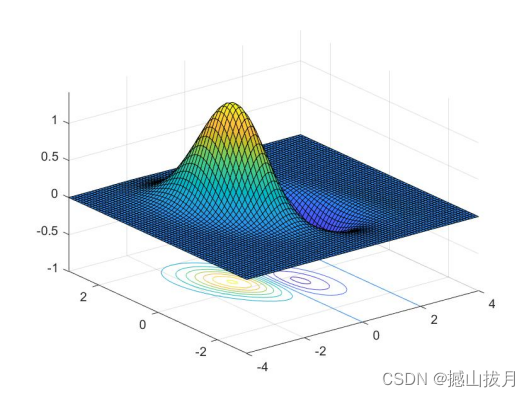
功能是绘制(X,Y,Z)生成的带有等高线的三维曲面图。
Demo :绘制带有等高线的三维曲面
绘制步骤:
1)指定横坐标和纵坐标的范围
2)利用函数meshgrid生成横坐标、纵坐标矩阵
3)根据已知函数生成竖坐标矩阵
4)利用函数surfc绘制曲面图
%示例代码:
[x,y]=meshgrid(-4:0.1:4,-3:0.1:3);
z=(x.^2-2*x).*exp(-x.^2-y.^2-x.*y);
surfc(x,y,z)
%运行结果
3)surfl
基本语法:surfl(X,Y,Z,C)
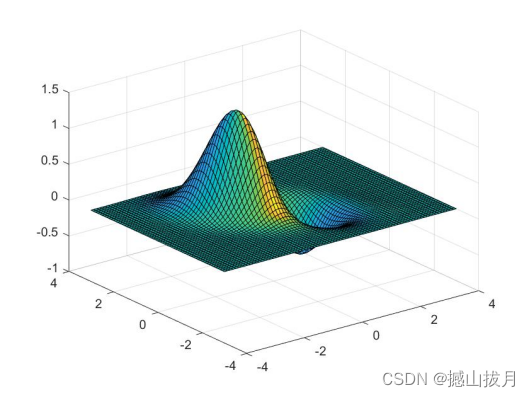
功能是绘制(X,Y,Z)生成的带有光照效果的三维曲面图。
Demo :绘制带有光照效果的三维曲面
绘制步骤:
1)指定横坐标和纵坐标的范围
2)利用函数meshgrid生成横坐标、纵坐标矩阵
3)根据已知函数生成竖坐标矩阵
4)利用函数surfl绘制曲面图
%示例代码:
[x,y]=meshgrid(-4:0.1:4,-3:0.1:3);
z=(x.^2-2*x).*exp(-x.^2-y.^2-x.*y);
surfl(x,y,z)
%运行结果
五、fsurf的基本用法
fsurf的功能是绘制二元函数fun的三维曲面,常见有下面的用法:
1、fsurf( fun ),横坐标和纵坐标的范围均是[-5,5]
2、fsurf( fun, xyinterval ),指定x和y的范围
3、fsurf(funx,funy,funz),参数方程形式的函数
4、fsurf(funx,funy,funz,uvinterval),参数方程形式的函数,并指定了参数的取值范围
Demo :绘制三维曲面图
%示例代码:
fun = @(x,y)(x.^2-2*x).*exp(-x.^2-y.^2-x.*y);
furf(fun)
%运行结果