hello，大家好

这里是第十期的概率论与数理统计的学习，我将用这篇博客去总结知识点和用C语言实现案例的过程。
在这里插入图片描述

本期知识点——期望

离散型随机变量的期望
连续型随机变量的期望
随机变量函数的期望
期望的性质

💦 期望的引入

随机变量的分布函数是对随机变量概率性质的完整的刻画，描述了随机变量的统计规律性。

但在实际问题中有时不容易确定随机变量的分布，也没那个必要，而我们只需要知道它的某些特征就行了。这些特征就是随机变量的数字特征，是由随机变量的分布所决定的常数。

例如，对一射手进行技术评定时，经常考察射击命中环数的平均值；检查一批棉花的质量时，所关心的是棉花纤维的平均长度等。也就是我们不需要了解一批东西全部的情况，那样太费时间，效率不高，而通过平均值就能看出一个整体的大概情况。这个平均值就是数学期望，简称为期望

下面开始知识总结

💦 知识总结

☁️ 离散型随机变量的期望

🌱 定义：设离散型随机变量的概率分布为 $P\{X=x_{i}\}=p_{i}~~~~~~~~i=1,2,...$
若级数 $\displaystyle\sum_{i}x_{i}p_{i}$ 绝对收敛，即 $\displaystyle\sum_{i}|x_{i}|p_{i}$ 收敛，则称 $\displaystyle\sum_{i}x_{i}p_{i}$ 为随机变量 $X$ 的期望，记为 $E (X)$ 。即 $E(X)=\displaystyle\sum_{i}x_{i}p_{i}$

为什么要保证那个级数绝对收敛？

在 $X$ 可列无限个值时，级数 $\displaystyle\sum_{i}x_{i}p_{i}$ 绝对收敛可以保证级数之值不因级数各项次序的改排而变化，这样 $E (X)$ 与 $X$ 取的值的人为排列次序无关。

如何理解期望和均值？

期望的定义就是随机变量 $X$ 的值乘上它表示的事件发生的概率。所以将 $E (X)$ 成为 $X$ 的均值更能反应这个概念的本质。

下面介绍几种常用的离散型随机变量的期望，后续都会用C语言实现

☀️ 两点分布

X	1	0
P	p	1-p

$E(X)=1\times p+0\times (1-p)=p$

☀️ 二项分布

设 $X$ ~ $B (n, p)$ ，概率分布为 $P\{X=k\}=C_{n}^kp^k(1-p)^{n-k}~~~~~~~~~k=0,1,2,...,n$

$E (X) = n p$

☀️ 泊松分布

设 $X$ ~ $P(\lambda)$ ，概率分布为 $P\{X=k\}=\frac{\lambda^{k}}{k!}e^{-\lambda}~~~~~~~k=0,1,2,...$
$E(X)=\lambda$

☁️ 连续型随机变量的期望

🌱 定义：设连续型随机变量 $X$ 的概率密度函数为 $f (x)$ ，若积分 $\int_{-\infty}^{+\infty}xf(x)dx$ 绝对收敛，即 $\int_{-\infty}^{+\infty}|x|f(x)dx$ 收敛，则称积分 $\int_{-\infty}^{+\infty}xf(x)dx$ 的值为随机变量 $X$ 的期望，记为 $E (X)$ ，即 $E(X)=\int_{-\infty}^{+\infty}xf(x)dx$

下面介绍几种常用的连续型随机变量的期望

☀️ 均匀分布

设 $X$ ~ $U [a, b]$ ，概率密度函数为 $f(x)=\begin{cases} \frac{1}{b-a}~~~~~~a\leq x\leq b\\ 0~~~~~~~~~其它\\ \end{cases}$
$E(X)=\int_{a}^b\frac{x}{b-a}dx=\frac12(a+b)$

☀️ 指数分布

设 $X$ 服从参数为 $\lambda$ 的指数分布，概率密度函数为 $f(x)=\begin{cases} \lambda e^{-\lambda x}~~~~x\geq 0\\ 0~~~~~~~~~~~~x<0\\ \end{cases}~~~~~~~\lambda>0$
$E(X)=\int_{0}^{+\infty}\lambda xe^{-\lambda x}dx=\frac1\lambda$

☀️ 正态分布

设 $X$ ~ $N(\mu,\sigma^2)$ ，概率密度函数为 $f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}},-\infty<x<+\infty$
$E(X)=\int_{-\infty}^{+\infty}\frac{x}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}dx$
令 $t=\frac{x-\mu}{\sigma}$ ，可得 $\int_{-\infty}^{+\infty}\frac{x}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}dx=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{+\infty}(\mu+\sigma t)e^{-\frac{t^2}{2}}dt=\mu$
最后可得 $E(X)=\mu$

☁️ 随机变量的期望总结

离散型

两点分布： $E (X) = p$
二项分布： $E (X) = n p$
泊松分布： $E(X)=\lambda$

连续型

均匀分布： $E(X)=\frac{1}{2}(a+b)$
指数分布： $E(X)=\frac1\lambda$
正态分布： $E(X)=\mu$

☁️ 随机变量函数的期望

🌱 定义：设 $g (x)$ 是连续函数， $Y$ 是随机变量 $X$ 的函数： $Y = g (X)$ 。

设 $X$ 是离散型随机变量，概率分布为 $P\{X=x_{i}\}=p_{i}~~~~~i=1,2...$ ，若 $\sum|g(x_{i})|p_{i}$ 收敛，则有 $E(Y)=E[g(X)]=\sum g(x_{i})p_{i}$
设 $X$ 是连续型随机变量，概率密度函数为 $f (x)$ ，若积分 $\int_{-\infty}^{+\infty}|g(x)|f(x)dx$ 收敛，则有 $E(Y)=E[g(x)]=\int_{-\infty}^{+\infty}g(x)f(x)dx$

根据上面的结论，我们可以推广到两个随机变量函数 $Z = g (X, Y)$ 的情形：

对离散型，设 $P\{X=x_{i},Y=y_{i}\}=p_{ij}~~~~~~~~i=1,2...~~~~j=1,2...$ ，则有 $E(Z)=E[g(X,Y)]=\sum_{i}\sum_{j}g(x_{i},y_{i})p_{ij}$
对连续型，设 $f (x, y)$ 是 $(X, Y)$ 的概率密度函数，则 $E(Z)=E[g(X,Y)]=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}g(x,y)f(x,y)dxdy$

☁️ 期望的性质

设 $c$ 是常数，则 $E (c) = c$
设 $k$ 是常数，则 $E (k X) = k E (X)$
$E (X + Y) = E (X) + E (Y)$
设 $X$ 与 $Y$ 相互独立，则 $E (X Y) = E (X) E (Y)$

💦 C语言实现案例

某种产品的次品率是0.1，检验员每天检验4次，每次随机抽取10件产品进行检验，如果发现其中的次品数大于1，则应调整设备。设各件产品是否为次品是相互独立的，求一天中调整设备次数的期望。

题目分析：题目的要求是只要有一次检验，十件产品中次品数大于1，就需调整设备。而一天中又要检验4天，并且求的是一天中调整设备的次数。所以我们可以先求出每一次检验后需要调整设备的概率，然后就可以转化为二项分布 $X$ ~ $B (n, p)$ ，求得一天中四次检验需要调整设备的期望。

#include <stdio.h>
// The algorithm of Combination ——组合的算法
int Combination(int n,int m)
{
	int sum = 1,p = 1;
	for( ; m > 0 ; m--)
	{
		sum *= n--;
		p *= m;
	}
	return sum/p;
}
// The algorithm of Binary Distrubution ——二项分布的算法
float BinDistrubution(int n,int k,float p)
{
	float _P;
	_P = Combination(n,k);
	for(int i = 0 ; i < k ; i++)
		_P *= p;
	for(int i = 0 ; i < n - k ; i++)
		_P *= (1 - p);
	return _P;
}

int main()
{
	float P = 1;
	float p;
	int n,tol;
	printf("Please input the probability of the defective rate:");
	scanf("%f",&p);
	printf("Please input the number of testing the equipments:");
	scanf("%d",&n);
	printf("Please input the number of products per inspection:");
	scanf("%d",&tol);
	for(int X = 0 ; X <= 1 ; X++)
	{
		P -= BinDistrubution(tol,X,p);
	}
	// 每次检验后需要调整设备的概率为：
	printf("The probability of every time we need to adjust the equipments after testing them is:%.4f\n",P);
	float P_y;
	P_y = n * P;
	// 一天中调整设备的次数的期望
	printf("The expectation of the day we adjust the equipments is :%.4f",P_y);
	return 0;
}

在这里插入图片描述
代码分析：代码主要的难度就是在二项分布的那个公式上，需要结合组合公式的算法才行，其它的就按照做题的思路来就行了。

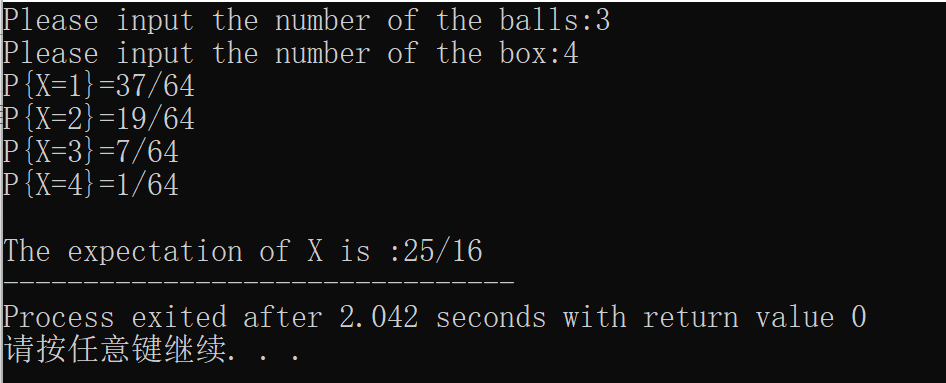
有4只盒子，编号为1，2，3，4，现有3个球，将球逐个独立地随机放入4只盒子中去。用 $X$ 表示其中至少有一个球的盒子的最小号码，求 $E (X)$ 。

题目分析：先来理解最后一句话，当 $X = 1$ 时表示1号盒子中至少有一个球，此时1为四个盒子中号码最小的那一个，当 $X = 2$ 时表示2号盒子中至少有一个球，此时2“应该为”最小号码，也就是说1号盒里就不会有元素了，当 $X = 3$ 时表示3号盒子中至少有一个球，此时3“应该”为最小号码，也就是说1和2号盒子里都没有球…

理解了最后一句话后这个题就简单了，每个球有4种放法，一共有3个球，也就是总共有 $4^3$ 种方法，然后若 $X = 1$ ，则 $P\{X=1\}=1-\frac{3^3}{4^3}=\frac{4^3-3^3}{4^3}$ …

#include <stdio.h>
#include <malloc.h>
#include <math.h>
// The algorithm of abbreviation ——约分的算法
void Abbreviation(int *a)
{
	while(a[0] % 2 == 0 && a[1] % 2 == 0)
	{
		a[0] /= 2;
		a[1] /= 2;
	}
	
	for(int i = 3 ;i <= a[1] / 2 ; i += 2)
	{
		while(a[0] % i == 0 && a[1] % i == 0)
		{
			a[0] /= i;
			a[1] /= i;
		}
	}
}

// Add up the points ——分数相加
int* add(int* a,int* b)
{
	if(a[0] == 0)
		return b;
	if(b[0] == 0)
		return a;
	int t = a[1];
	a[1] *= b[1];
	a[0] *= b[1];
	a[0] += b[0] * t;
	Abbreviation(a);
	return a;	
}

int main()
{
	int ball,box;
	printf("Please input the number of the balls:"); // 输入球的数量
	scanf("%d",&ball);		
	printf("Please input the number of the box:");	 // 输入盒子的数量
	scanf("%d",&box);
	int E_X[2] = {0};
	// X denotes the random variable ——X表示随机变量
	for(int X = 1 ; X <= box ; X++)				// The prosibible values of X ——X可能取的值
	{
		int coe[2];
		coe[0] = pow(box - X + 1,ball) - pow(box - X,ball);
		coe[1] = pow(box,ball);
		Abbreviation(coe);
		printf("P{X=%d}=%d/%d\n",X,coe[0],coe[1]);
		// According to the formula of the Expectation ——根据期望的公式
		// x_i*p_i
		coe[0] *= X;
		int *t = add(E_X,coe);
		E_X[0] = t[0];
		E_X[1] = t[1];
	}
	printf("\n");
	printf("The expectation of X is :%d/%d",E_X[0],E_X[1]);
	return 0;
}

在这里插入图片描述
代码分析：还是老样子，对于一个需要用分数来表示的题，我们用一个大小为2的一维数组来分别存储它的分子和分母，然后进行相关的运算即可。

那些啥组合公式的代码、约分代码我在这类专栏的前面博客中写过，所以这里就直接拿过来用了。

设二维离散型随机向量 $(X, Y)$ 的概率分布如下表所示，求 $Z=X^2+Y$ 的期望。

X\Y	1	2
1	0.125	0.25
2	0.5	0.125

题目分析：由题知，再结合前面总结的知识点，设 $g(x,y)=x^2+y$ ，那么有：

$X = 1, Y = 1$ ： $Z = g (1, 1) = 2$
$X = 1, Y = 2$ ： $Z = g (1, 2) = 3$
$X = 2, Y = 1$ ： $Z = g (2, 1) = 5$
$X = 2, Y = 2$ ： $Z = g (2, 2) = 6$

则 $E(Z)=2\times 0.125+3\times 0.25+5\times 0.5+6\times0.125=4.25$

#include <stdio.h>
#include <malloc.h>
#include <math.h>
int main()
{
	// Use an array to restore the datas of probability distrubution ——用一个数组来存储概率分布中的数据
	float **D;
	D = (float **) malloc (sizeof(float *) * 2);
	for(int i = 0 ; i < 2 ; i++)
		D[i] = (float *) malloc (sizeof(float *) * 2);
	// 请按行输入概率分布的数据：
	printf("Please input the values of the probability distrubution by line:\n");
	for(int i = 0 ; i < 2 ; i++)
	{
		for(int j = 0 ; j < 2 ; j++)
		{
			scanf("%f",*(D + i) + j);	
		}
	}
	// E_X denotes the expectation of X ——E_X表示X的期望
	float E_X = 0;
	printf("\n");
	// 这个概率分布为：
	printf("The probability distrubution is :\n");
	for(int i = 0 ; i < 2 ; i++)
	{
		for(int j = 0 ; j < 2 ; j++)
		{
			printf("%.3f   ",*(*(D + i) + j));
			// According to the formula of expectation ——根据期望的公式
			// xi*pi
			E_X += (pow(i + 1,2) + j + 1) * (*(*(D + i) + j));
		}
		printf("\n");
	}
	// X的期望为：
	printf("The expectation of X is:%.2f",E_X);
	return 0;
}