根轨迹法:通过求开环零点和开环极点,来画出闭环极点在S平面的位置。
也是用来判断系统稳定性的。
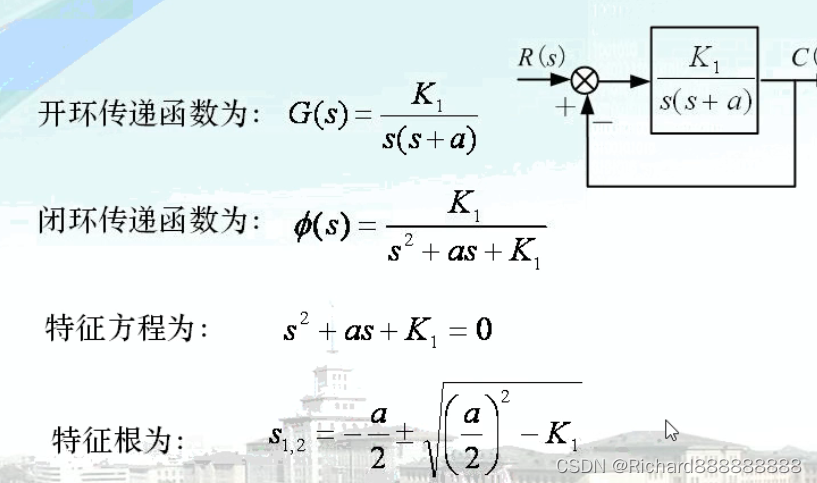

 定义:根轨迹是指系统特征方程式的根(闭环极点)随系统参量变化 在S平面
定义:根轨迹是指系统特征方程式的根(闭环极点)随系统参量变化 在S平面
上运动而形成的轨迹。
开环传递函数里边的一个参数,或者特征方程式里边的一个参数发生变化 的时候,
它的特征根或者是闭环极点,在S平面上运行所形成的轨迹。
 幅值条件是相差+-180度。
幅值条件是相差+-180度。
有m个零点,和n个极点。
G(S)叫前项通道的传递函数。
H(s)叫反馈通道的传递函数。
开环传递函数是G(S)*H(S)
因为闭环传递函数G(S)H(s)+1=0,
如果开环传函是如下的函数
 那么它的相角条件和幅值条件是怎
那么它的相角条件和幅值条件是怎
么样的?
幅值条件
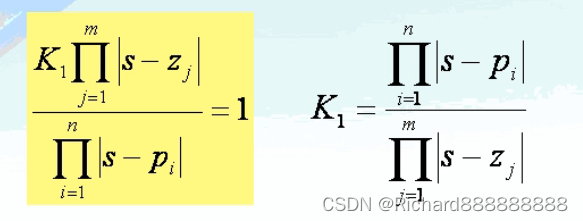
相角条件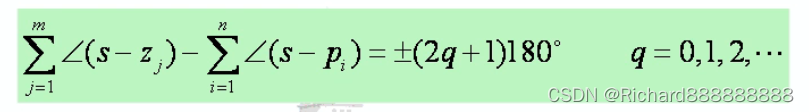
开环传递函数是已知的,那么它一定能表示成零极点形式。
如下是具体的系统
, H(S)=1
G(S)H(S)=1
相角条件S对零点相角的和-S对极点相角的和。
没有零点。
极点:0,-a
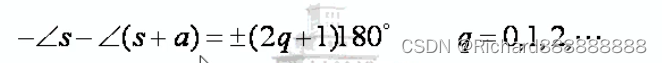
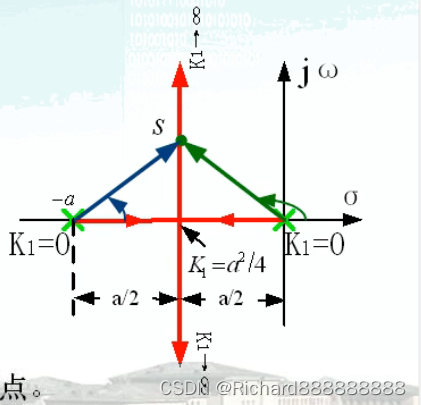
根轨迹如上图。
绿线和蓝线的角相加等于180度
绿线是s点到0点的线。
蓝线是s点到-a的线。
绘制根轨迹的一些规则
规则一、系统根轨迹的各条分支是连续的,而且对称于实轴。
规则二、当K1=0时,根轨迹的各条分支从开环极点出发;当K1-->无穷时,
有m条分支趋向于开环零点,另外有n-m条分支趋向无穷远处。(n是极点个数,m是零点个数)
时,S->零点。
规则三 在S平面实轴的线段上存在根轨迹的条件是,在这些线段右边的开环零
点和开环极点的数目之和为奇数。
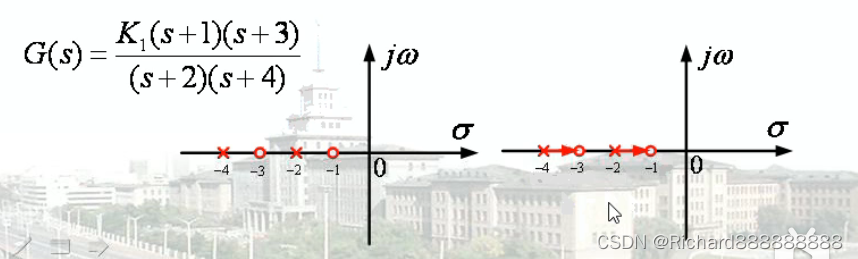
规则三的意思是如上图,从右开始数,如果零点和极点之和是奇数,那么这段线段
是有根轨迹的。具体如图上所示。箭 头是极点指向零点。
极点重合的情况的根轨迹
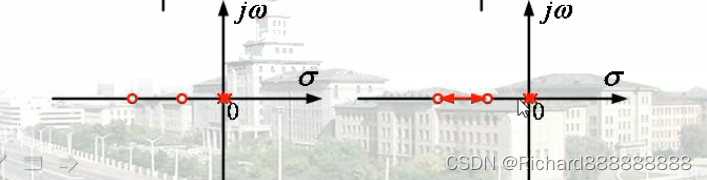
永远是极点指向零点。
规则四 根轨迹中(n-m)条趋向无穷远处分支的渐近线相角为
(渐近线与实轴交的角度)

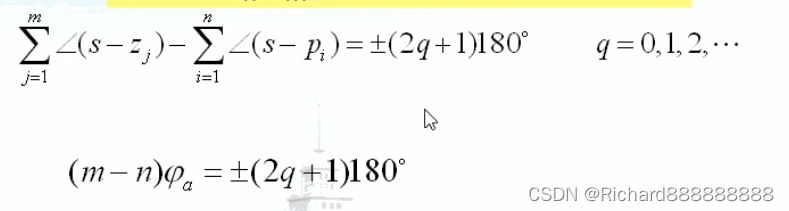
渐近线会趋向于无穷远,渐近线上的点,s点很远,很远。
n-m=1
n-m=2
n-m=3
n-m=4
渐近线本身一定是对称于实轴。
规则五 伸向无穷远处的根轨迹的渐近线与实轴交于一点,交点的坐标为
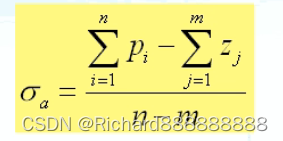
例题:

写出开环零点和极点
零点没有
极点有三个
s(s+1)(s+2)=0
p1=0,p2=-1,p3=-2
n=3(极点个数)
m=0(零点个数)
(2) 实轴上根轨迹 (,-2] [-1,0]
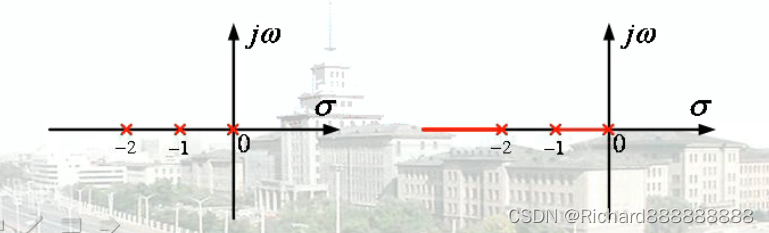
起始于开环极点,终止于开环零点,或者是沿着渐近线的方向趋于无穷远。
n-m=3,有三条渐近线。
(3) 求渐近线

与实轴的交点(所有开环极点的和-开环零点的和)
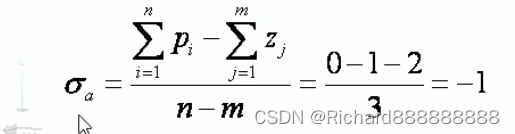
图形如下
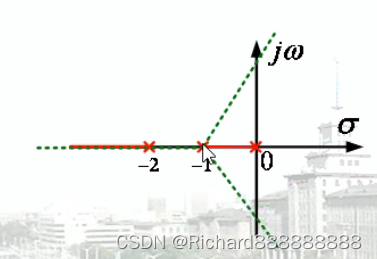
matlab 根轨迹图
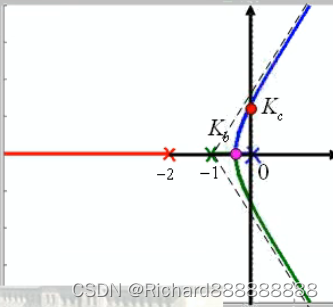
这里没有零点,所以终止于无穷远。
K1<Kb,三个闭环极点全部在实轴上,如果给他加阶跃信号,会逐渐稳定在稳定值上,
没有振荡。这种叫过阻尼。
K1=Kb,对应在粉红色的点,相当于临界状态。 临界阻尼。
Kb<K1>Kc (欠阻尼) 闭环极点相当于在复频面上。这时,时域响应中,就有震荡成分。
K1>Kc的时候,系统就不稳定了。
规则六 复平面上根轨迹的分离点必须满足方程
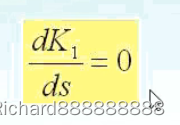
上述条件只是确定分离点的必要条件,不是充分条件。
若实轴上两开环极点之间存在根轨迹,则一定存在分离点;
若实轴上相邻开环零点之间存在根轨迹,则一定存在汇合点;
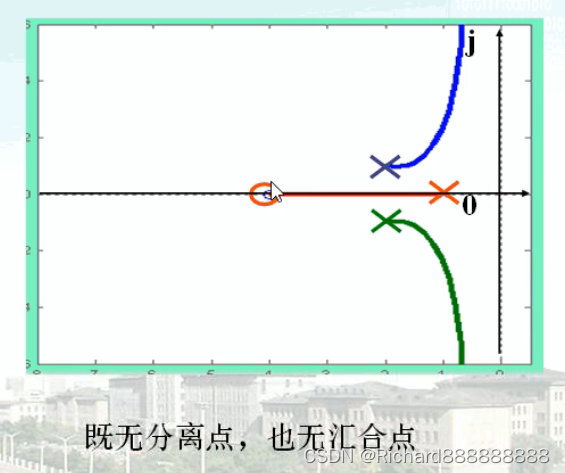
若实轴上的根轨迹处在开环零点和开环极点之间,可以既无分离点也无
汇合点,也可能既有分离点也有汇合点;
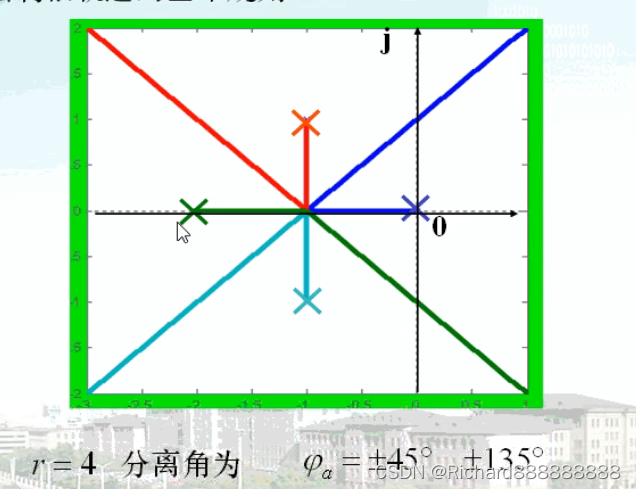
分离角和汇合角:分离点或汇合点的切线与正实轴的夹角。

如图
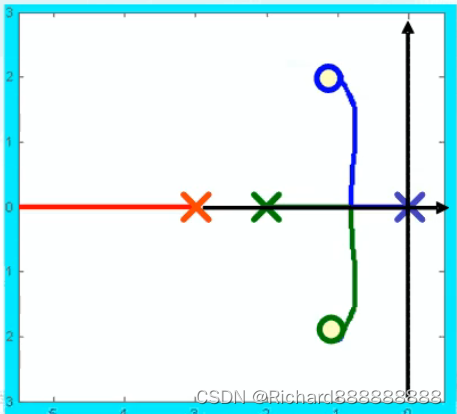
有分离点
m=3
n=2
有(m-n)1个渐近线
两个极点之间如果有根轨迹的话,一定要分开。
图二
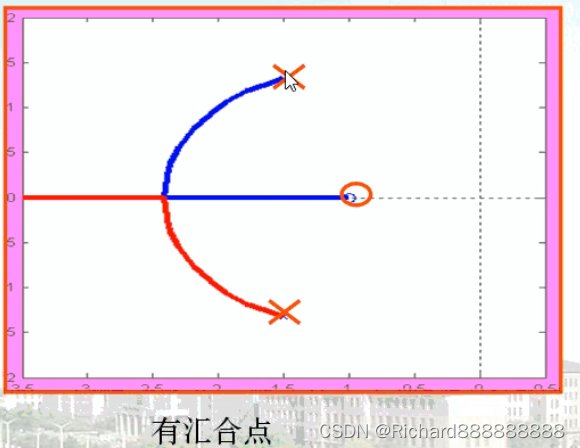
m=2
n=1
有一个根轨迹。
根轨迹一定是上下对称的。
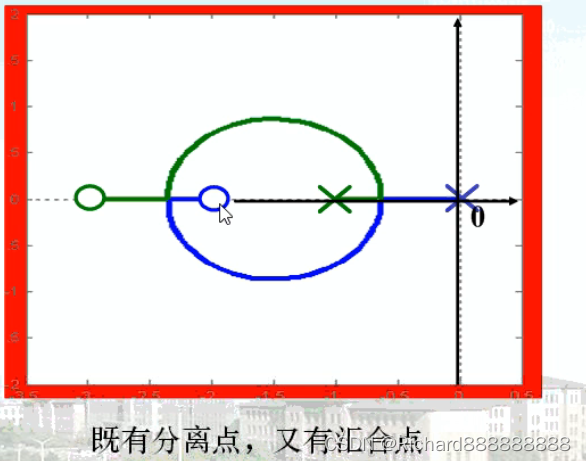

从(,一2]有根轨迹,从[-1,0]有根轨迹。
[-2,-1]没有根轨迹,所以值-1.577需要舍弃。
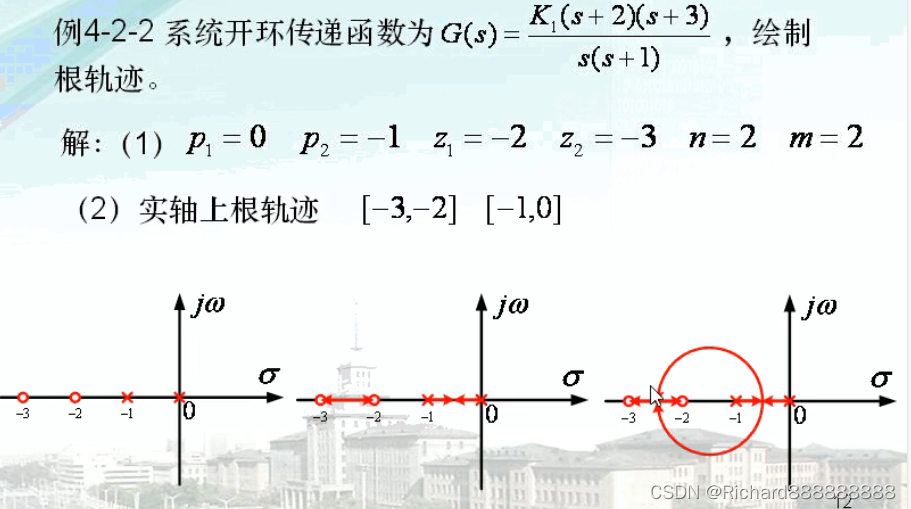

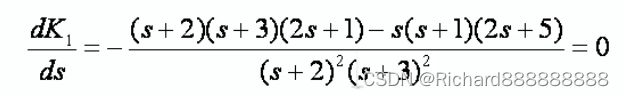
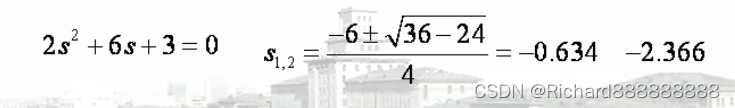

(1) 求出极点,零点,以及数量
(2) 确定实轴上有根轨迹的区域
(3)画出根轨迹图(注意画根轨迹,一定要上下对称 )
(4)求分离点,对K1进行求导,求出方程的根
(5)判断求出的根,在不在根轨迹上。
(6)求出K1的值
二绘制根轨迹的基本规则
出射角——指起始于开环极点的根轨迹在起点处的切线与正实轴的夹角。
入射角——指终止于开环零点的根轨迹在终点处的切线与正实轴的夹角。
规则七
在开环复数极点处根轨迹的出射角为

在开环零点处根轨迹的入射角为
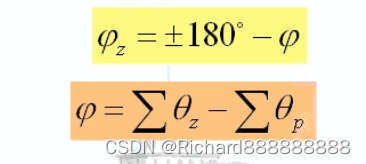
为其它开环零、极点对该出射点或入射点提供的相角。
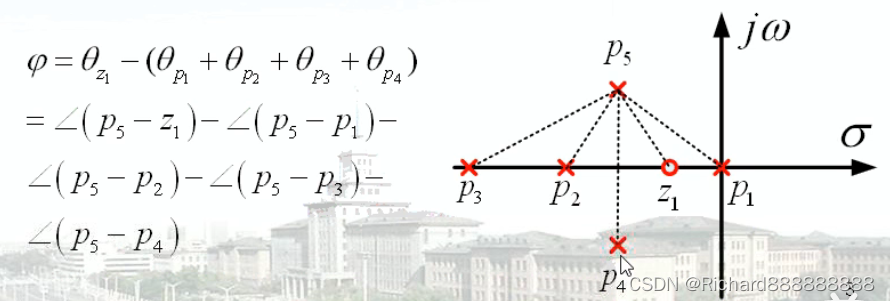
z是零点,p是极点。
所有零点相角的和-所有极点相角的和
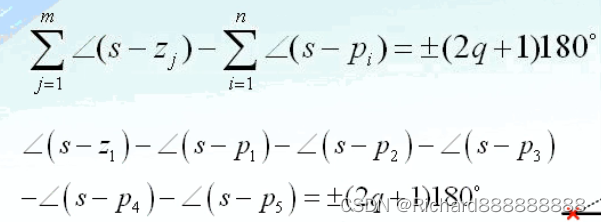
当s-->p5(当s趋近于p5)
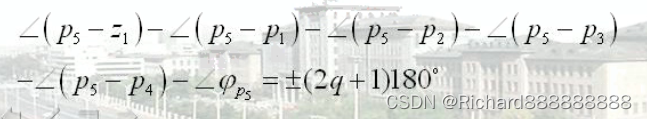
规则八
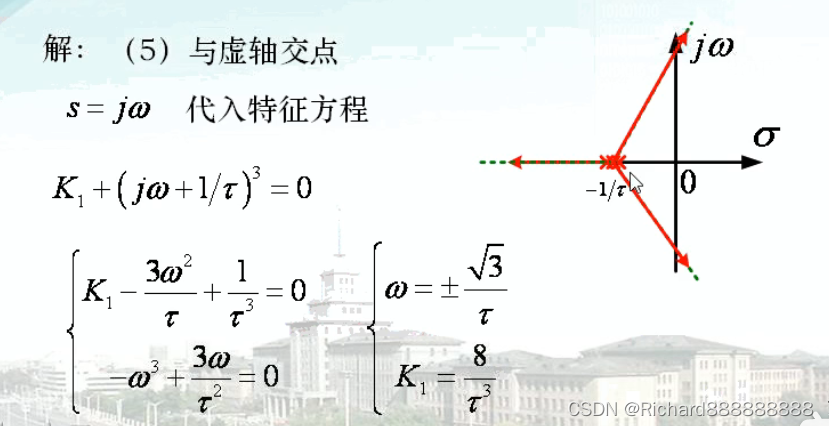
根轨迹与虚轴的交点可用s=jw代入特征方程求解,或都利用劳斯判据确定。
根轨迹与虚轴相交,处于临界稳定状态。

求与虚轴的交点
s=jw 代入特征方程 s(s+1)(s+2)+k1=0
jw(jw+1)(jw+2)+K1=0
实部
虚部
根据上面两个方程求出
如果K1=0,那就虚部也为0,就没意义了。
第二种方法就是用劳斯判据求虚轴交点
K1=6, 通过辅助方程求根

规则九 根轨迹上每一点所对应的参数
值可以按幅值条件来计算。
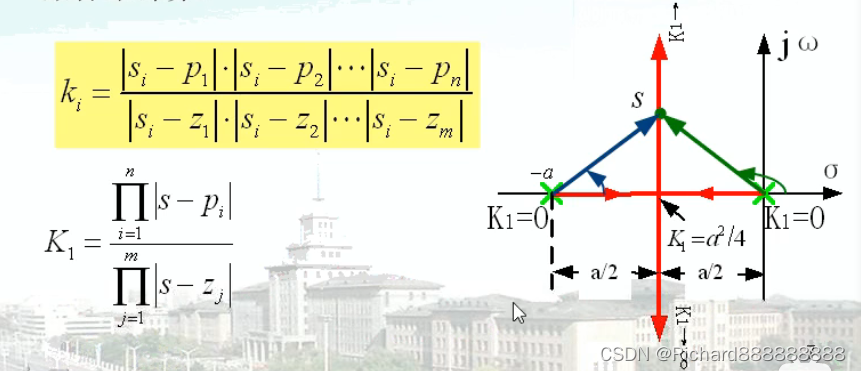
如下图,KC用规则8求,而Kb则用规则9求。

例题
将s=jw代入特征方程,相当于复数等于0
根轨迹是沿着渐近线走。
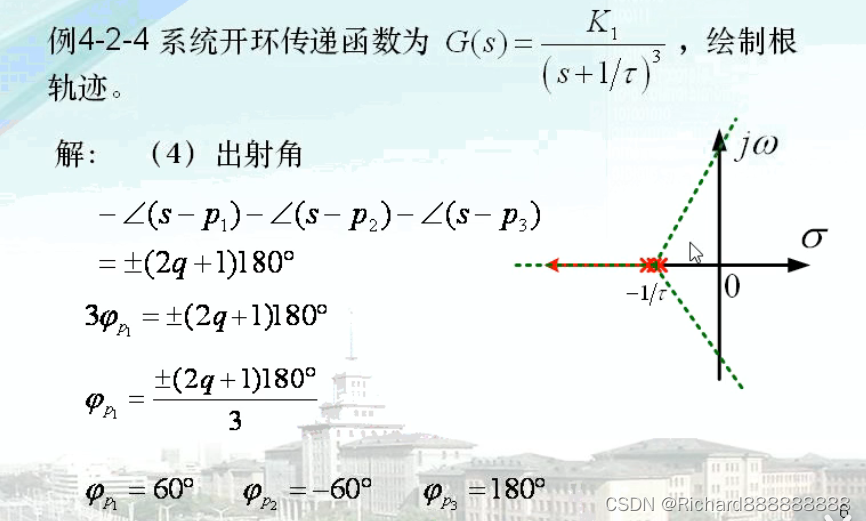
例题
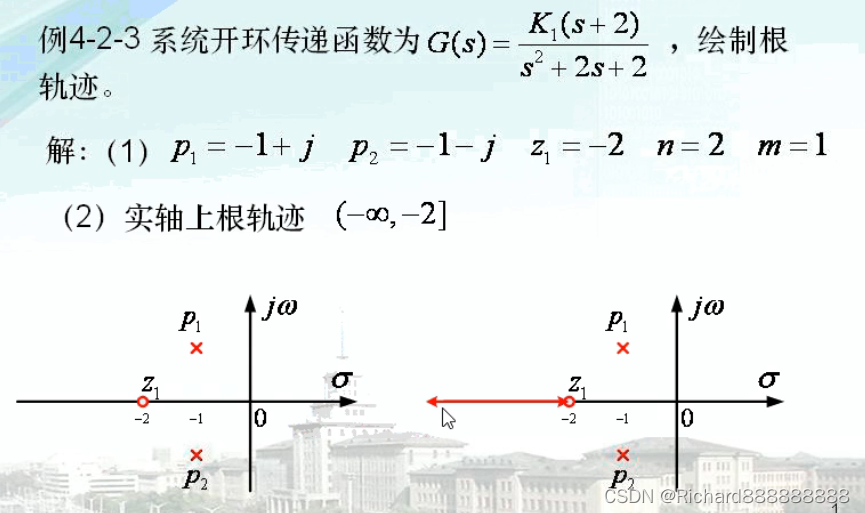
虚轴上出现的零极点是成对的,不改变实轴上的奇偶性。
起始于极点,终止于零点或远穷远。
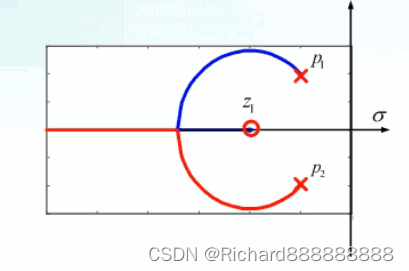
1+G(S)=0
求出特征方程
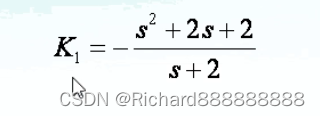
对K1求导
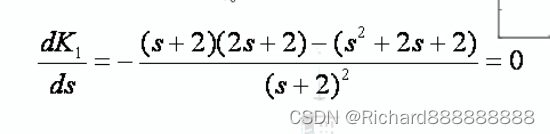
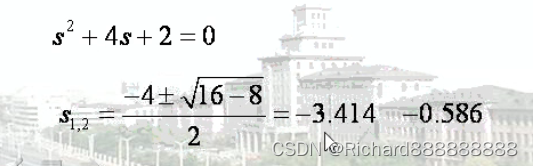
分子为0。
出射角可以通过相角条件来求。
求出射角
p1的切线也就是出射角。
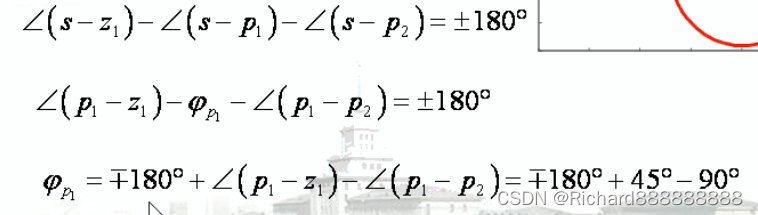






![2023年中国超硬材料制品分析及超硬刀具市场规模分析[图]](https://img-blog.csdnimg.cn/img_convert/c6b209830e68c87b18ab77b174bc6a9a.png)