题目

n*m(1<=n,m<=2e5)的棋盘，有k(k<=min(n*m,2e5))个特殊位置，

初始时在(1,1)位置，Chaneka和Bhinneka两人玩游戏，Chaneka先手，

当你在(x,y)位置时，下一步可以走到同一行靠右的位置(x'=x,y'>y)或同一列靠下的位置(x'>x,y'=y)

保证(1,1)不是特殊位置，若走到特殊位置则获胜，若无法操作则失败

问双方都最优操作下，谁获胜

思路来源

https://www.cnblogs.com/cjjsb/p/17693794.html#i-imagination-castle

题解

首先会想到n*m的sg打表，sg值转移可以大于1，但是本题是没有必要的，

只需关注sg=0和sg=1两个值就可以了，也就是先手必胜和先手必败态

对于特殊位置，由于先手站在其同行左侧或者同列上侧，走一步就赢了

后手同理，所以两人不会往这些地方上走，

对于每个特殊位置，可以给其同行左侧和同列上侧这些地方打X

对剩下的图中O的部分跑sg，再判断(1,1)是不是一个先手必败点，

画圈的地方是先手必败点，复杂度O(n*m)

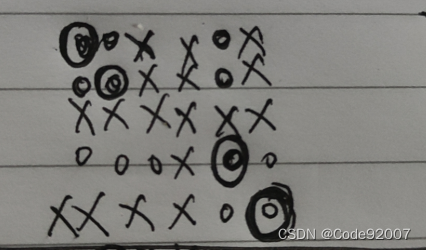
考虑我们一开始最右下角，倒着推sg值的过程，

1. (x,y)在右下角，必败，sg(x,y)=0，同时第x行左侧和第y列上侧所有sg值为1，接着考虑(x-1,y-1)

2. (x,y)被X覆盖，要么当前位置有棋子，要么右侧有棋子，要么下方有棋子

①如果当前位置有棋子，说明当前位置是一个必败态，接着考虑(x-1,y-1)，和第一种情况类似

②如果仅右侧有棋子，说明当前位置必胜态，同行左侧都是必胜态，同行不可能再出现必败态了，但同列下方都是必胜态，还有可能在上方出现必败态，接着考虑(x-1,y)

③如果仅下放有棋子，说明当前位置必胜态，同列上侧都是必胜态，同列不可能再出现必败态了，

但同行右侧都是必胜态，还可能在左侧出现必败态，接着考虑(x,y-1)

然后发现，这么移动指针时，中途经过的点，只可能有这两种情况，

要么(x,y)是一个必败态，要么(x,y)被X覆盖，简单证明没有被X覆盖的一定是必败态

1. 因为当(x,y)没有被X覆盖时，(x,y)右侧、下方都没有棋子，无法直接一步获胜

2. 间接获胜的情形也是不存在的，是因为上一个必败态(x',y')产生后，接下来考虑的是(x'-1,y'-1)

反过来看，当考虑(x,y)的时候，x行右侧、y列下侧是没有必败态的，

无法转移到必败态，所以当前就是必败态

心得

妙妙cf2300思维题，利用dp的递推以及全图只有min(n,m)个额外的必败态点，将两维拆开

巧妙的通过双指针找到所有额外的必败态点，从而确定n*m个值的sg状态

对于一个n*m的矩形，要么砍掉最后一行，要么砍掉最后一列，要么同时砍掉，去求更小的子局面

代码

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pb push_back
#define all(a) a.begin(),a.end()
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
std::mt19937_64 gen(std::chrono::system_clock::now().time_since_epoch().count());
ll get(ll l, ll r) { std::uniform_int_distribution<ll> dist(l, r); return dist(gen); }
const int N=2e5+10,INF=0x3f3f3f3f;
int n,m,k,x,y,r[N],c[N];
bool sol(){
	sci(n),sci(m),sci(k);
	rep(i,1,k){
		sci(x),sci(y);
		r[x]=max(r[x],y);
		c[y]=max(c[y],x);
	}
	for(x=n,y=m;x>=1 && y>=1;){
		if(y<=r[x] && x<=c[y])x--,y--;
		else if(y<=r[x])x--;
		else if(x<=c[y])y--;
		else{
			if(x==1 && y==1)return 0;
			x--,y--;
		}
		//printf("x:%d y:%d\n",x,y);
	}
	return 1;
}
int main(){
	puts(sol()?"Chaneka":"Bhinneka");
	return 0;
}