数学知识总结

素数

质数/素数定义

在大于1的整数中，如果只包含1和本身这两个约数，就被称为质数，或者叫素数

判断素数（试除法）

约数有一个重要的性质：

假设n代表数字，d代表n的一个约数

即d能整除n(d|n)

那么n/d为n的另外一个约数

即n/d能整除d(n/d | n)

简单思路：

模板：

bool is_prime(int n)
{
    if (n <= 1) return false;
    
    for (int i = 2; i <= n / i; i ++ )
      if (n % i == 0) return false;
     
    return true;
}

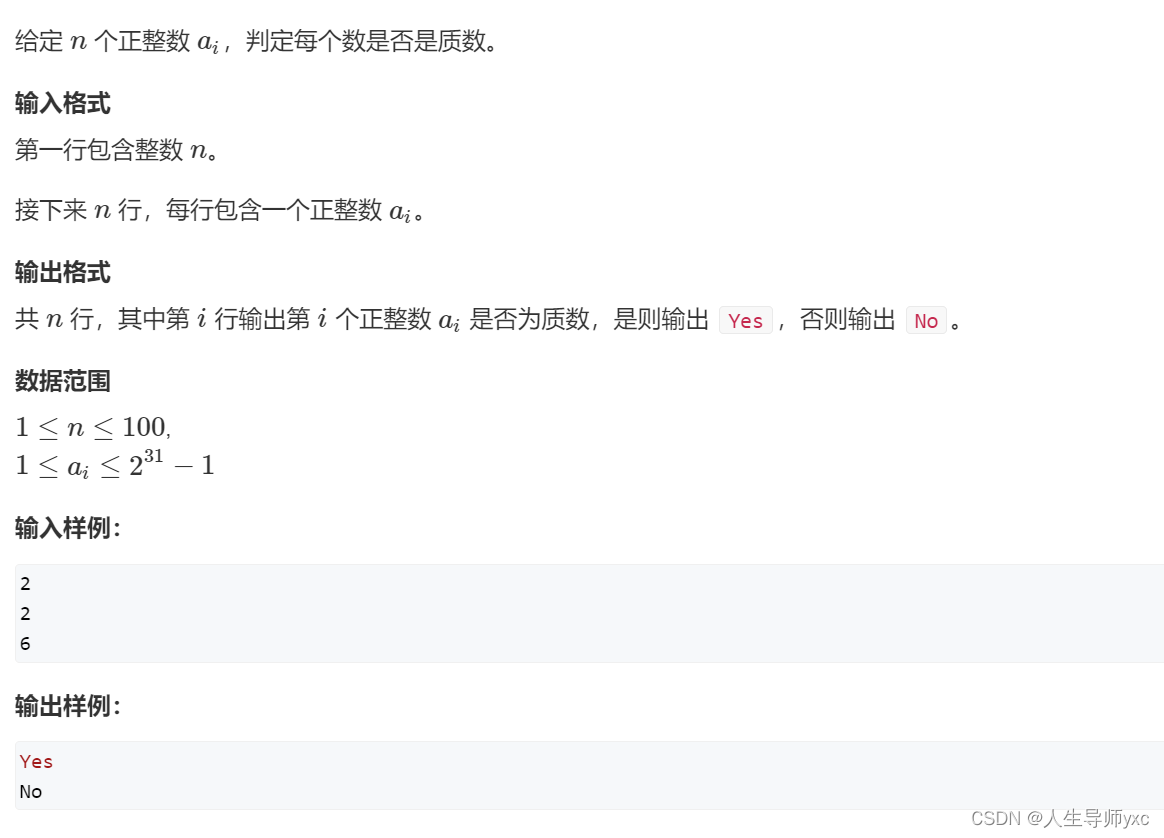
866. 试除法判定质数

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

bool is_prime(int n)
{
    if (n <= 1) return false;
    
    for (int i = 2; i <= n / i; i ++ )
      if (n % i == 0) return false;
     
    return true;
}
int main()
{
    int n;
    cin >> n;
    
    while (n --)
    {
        int a;
        cin >> a;
        if (is_prime(a)) puts("Yes");
        else puts("No");
    }
    
    return 0;
}

分解质因数（试除法）

从小到大枚举所有的数

为什么不需要判断是否为质因子？

因为i是n的因子，即n是i的倍数，当枚举的到i时，n中已经不包含有2~i-1的因子，即i中也不包含，2~i-1的因子，所以i是质数

n中最多只包括一个大于sqrt(n)的质因子

如果最后剩下一个大于1的数，那就是大于sqrt(n)的质因子

模板：


void divide(int n)
{
    for (int i = 2; i <= n / i; i ++ )
    {
        if (n % i == 0)
        {
            int cnt = 0;
             while (n % i == 0)
             {
                 cnt ++;
                 n /= i;
             }
             printf("%d %d\n", i, cnt);
        }
    }
    if (n > 1) printf("%d %d\n", n, 1);
    printf("\n");
}

acwing 867. 分解质因数

#include <iostream>
#include <algorithm>

using namespace std;


void divide(int n)
{
    for (int i = 2; i <= n / i; i ++ )
    {
        if (n % i == 0)
        {
            int cnt = 0;
             while (n % i == 0)
             {
                 cnt ++;
                 n /= i;
             }
             printf("%d %d\n", i, cnt);
        }
    }
    if (n > 1) printf("%d %d\n", n, 1);
    printf("\n");
}

int main()
{
    int n;
    scanf("%d", &n);
    
    while (n --)
    {
        int a;
        scanf("%d", &a);
        divide(a);
    }
    
    return 0;
}

埃氏筛法

算法思路：

模板：

void gets_prime(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i])
        {
            cnt ++;
            for (int j = i * 2; j <= n; j += i) st[j] = true;
        }
    }
}

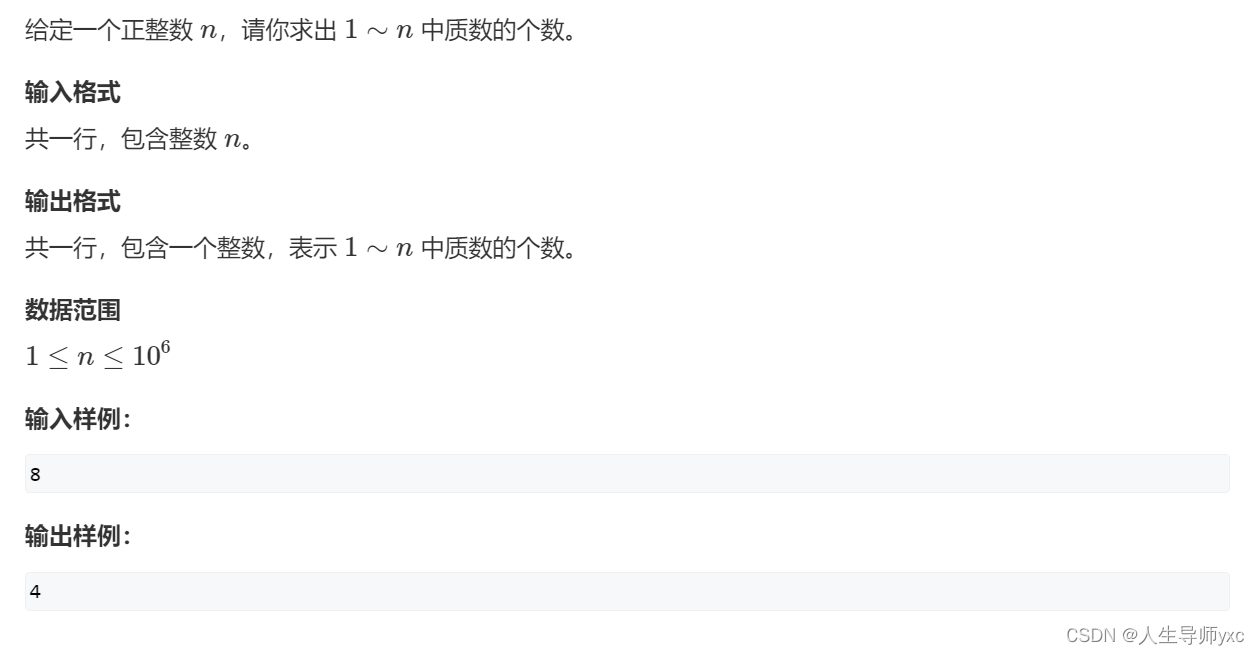
868. 筛质数

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;
const int N = 1000010;
bool st[N];
int cnt;

void gets_prime(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i])
        {
            cnt ++;
            for (int j = i * 2; j <= n; j += i) st[j] = true;
        }
    }
}
int main()
{
    int n;
    cin >> n;
    gets_prime(n);
    cout << cnt << endl;
}

线性筛（欧拉筛法）

算法思路：

模板：

void oula(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++] = i;
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            st[i * primes[j]] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

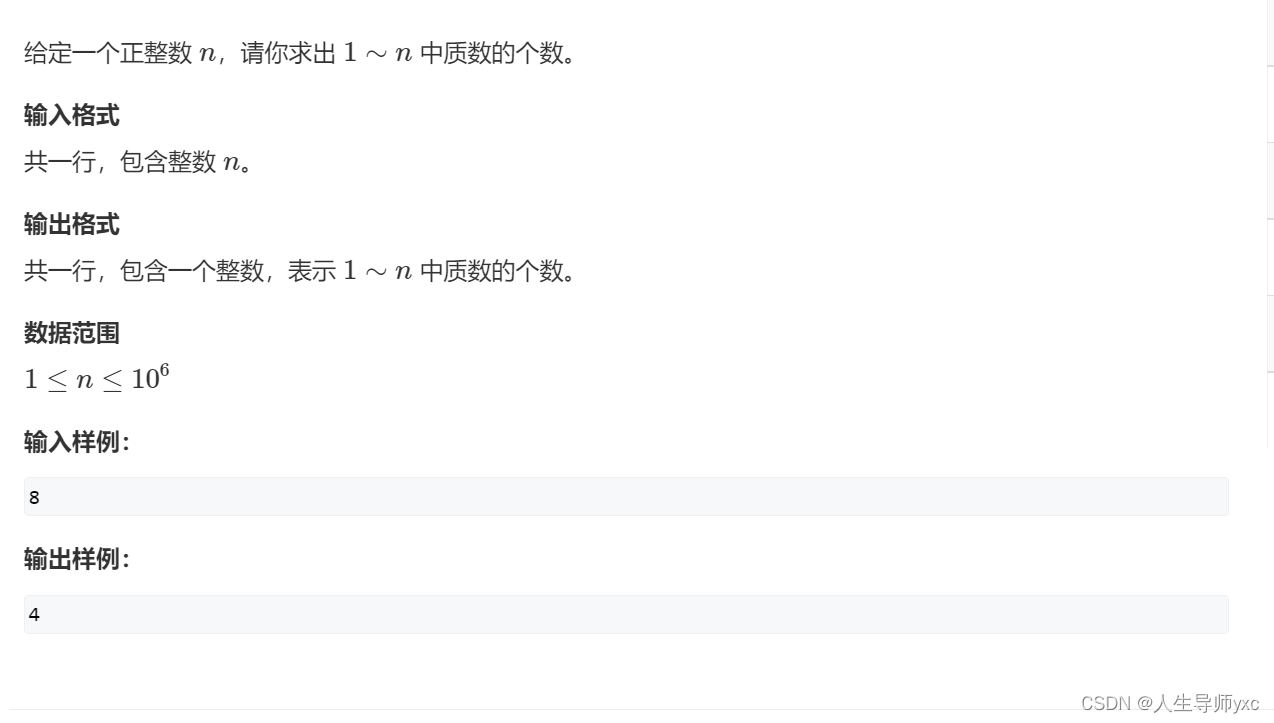
868. 筛质数

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1000010;
int primes[N];
bool st[N];
int cnt;

void oula(int n)
{
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i]) primes[cnt ++] = i;
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            st[i * primes[j]] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

int main()
{
    int n;
    cin >> n;
    oula(n);
    cout << cnt << endl;
}

约数

试除法

思路：

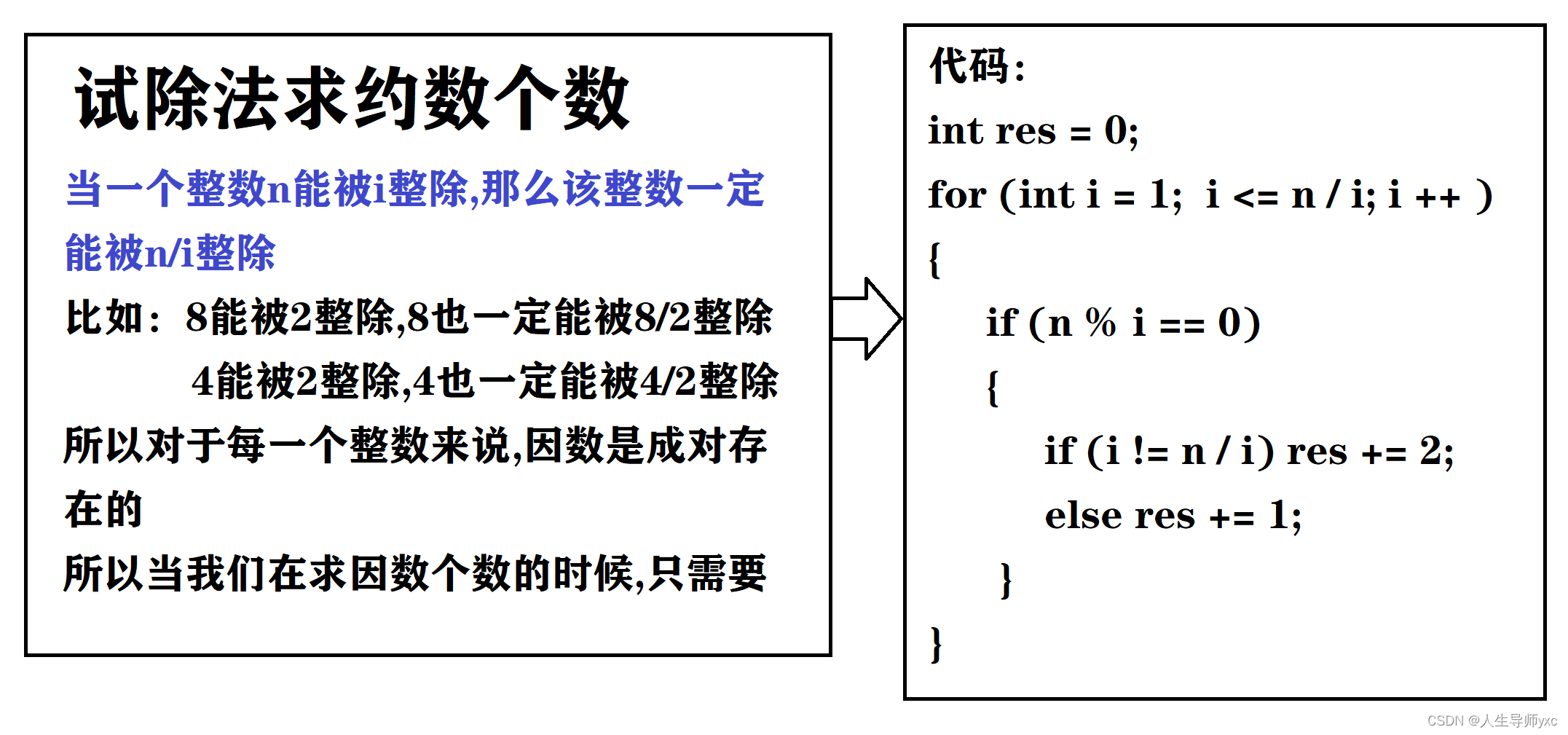
模板：


int res = 0;
for (int i = 1; i <= n / i; i ++ )
{
    if (n % i == 0)
    {
        if (i == n / i) res += 2;
        else res += 1;
    }
}

—————————————这就是纯暴力解法，时间复杂度高——————————————

通过算数基本定理来求约数个数

思路：

模板：

unordered_map<int, int> prime;//prime[质因子] = 次方
for (int i = 2; i <= x / i; i ++ )//分解质因数
{
    if (x % i == 0)
    {
        while (x % i == 0)
        {
            x /= i;
            prime[i] ++;
        }

    }
}
if (x > 1) prime[x] ++;
long long res = 1;
for (auto it = prime.begin(); it != prime.end(); it ++)
{
    res = res * (prime->second + 1);
}

870. 约数个数

输入样例：

代码展示：

#include <iostream>
#include <algorithm>
#include <cstring>
#include <unordered_map>

using namespace std;

typedef long long LL;
const int mod = 1e9 + 7;

int main()
{
   int n;
   scanf("%d",&n);
   
   unordered_map<int, int> prime;
   
   while (n --)
   {
       int x;
       cin >> x;
       for (int i = 2; i <= x / i; i ++ )
       {
            while (x % i == 0)
            {
                x /= i;
                prime[i] ++;
            }
       }
       if (x > 1) prime[x] ++;
   }
   
   LL res = 1;
   for (auto p : prime) res = res * (p.second + 1) % mod;
   printf("%lld\n",res);
}

————————————————————next—————————————————————

通过算术基本定理求约数之和

思路：

模板：

unordered_map<int, int> prime;//prime[质因子] = 次方
for (int i = 2; i <= x / i; i ++ )//分解质因数
{
    if (x % i == 0)
    {
        while (x % i == 0)
        {
            x /= i;
            prime[i] ++;
        }

    }
}
if (x > 1) prime[x] ++;
long long res = 1;
for (auto it = prime.begin(); it != prime.end(); it ++)
{
     int a = it->first, b = it->second;
     long long t = 1;
     for (int i = 0; i < b; i ++) t = t * a + 1;
     res = res * t;  
}

871. 约数之和

输入样例：

代码展示：

#include <iostream>
#include <algorithm>
#include <cstring>
#include <unordered_map>

using namespace std;

typedef long long LL;
const int mod = 1e9 + 7;

int main()
{
    int n;
    scanf("%d",&n);
    
    unordered_map<int, int> prime;
    
    while (n --)
    {
        int x;
        cin >> x;

        for (int i = 2; i <= x / i; i ++ )
        {
            while (x % i == 0)
            {
                prime[i] ++;
                x /= i;
            }
        }
        if (x > 1) prime[x] ++;
    }
    LL res = 1;
    for (auto p : prime)
    {
        int a = p.first, b = p.second;
        LL t = 1;
        for (int i = 0; i < b; i ++ ) t = (t * a + 1) % mod;
        res = res * t % mod;
    }
   cout << res << endl;
}

———————————————————next—————————————————————

求最大公约数

思路：

模板：

 int gcd(int a, int b)
{
    return b ? gcd(b, a % b) : a;
}

输入样例：

2
3 6
4 6

AcWing 872. 最大公约数

代码展示：

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

int gcd(int a, int b)
{
    return b ? gcd(b, a % b) : a;
}

int main()
{
    int n;
    cin >> n;
    
    while (n --)
    {
        int a, b;
        cin >> a >> b;
        int ans = gcd(a, b);
        cout << ans << endl;
    }
    
    return 0;
}

欧拉函数

基本思路：

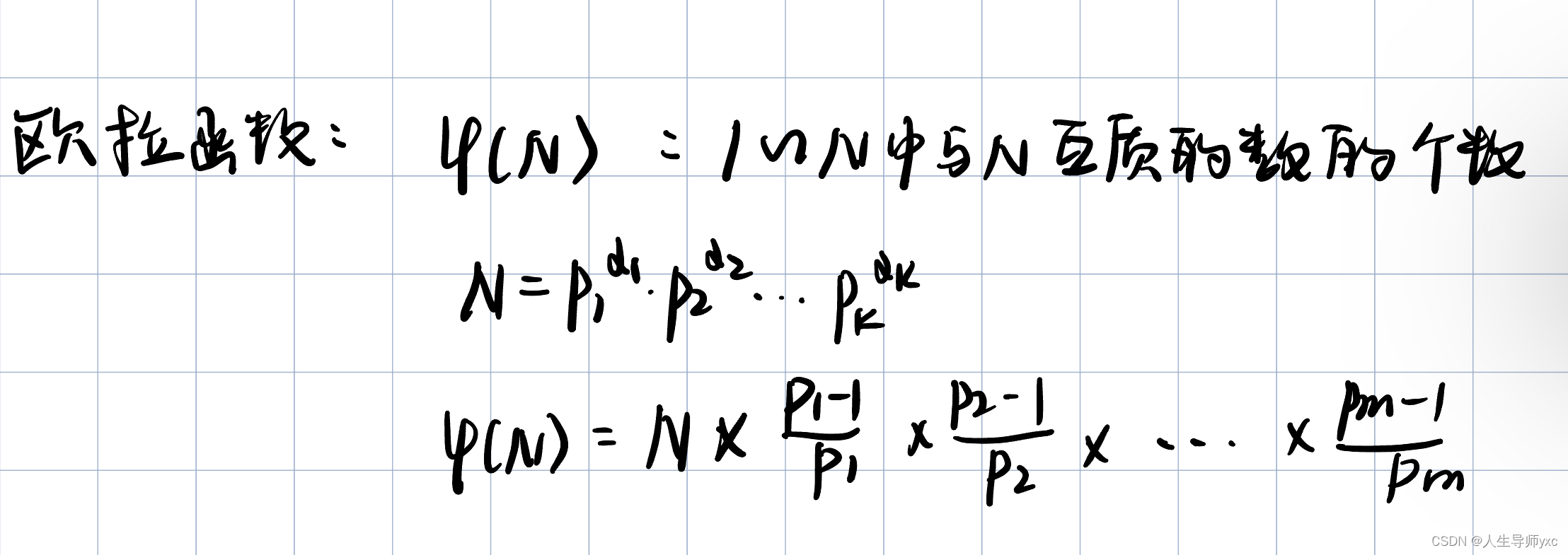
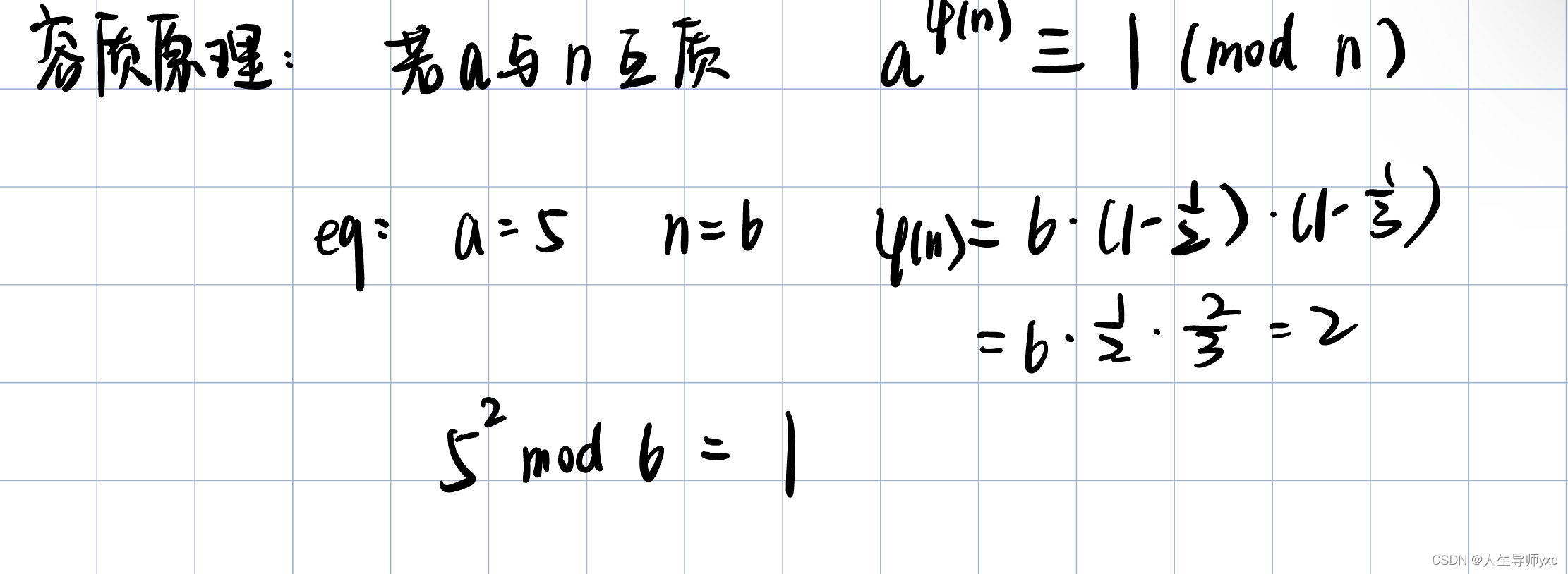
模板（暴力）：

long long res = x;
for (int i = 2; i <= x / i; i ++ )
{
    if (x % i == 0)
    {
        while (x % i == 0) x /= i;
        res = res * (i - 1) / i;
    }
}
if (x > 1) res = res * (x - 1) / x;

Acwing873. 欧拉函数

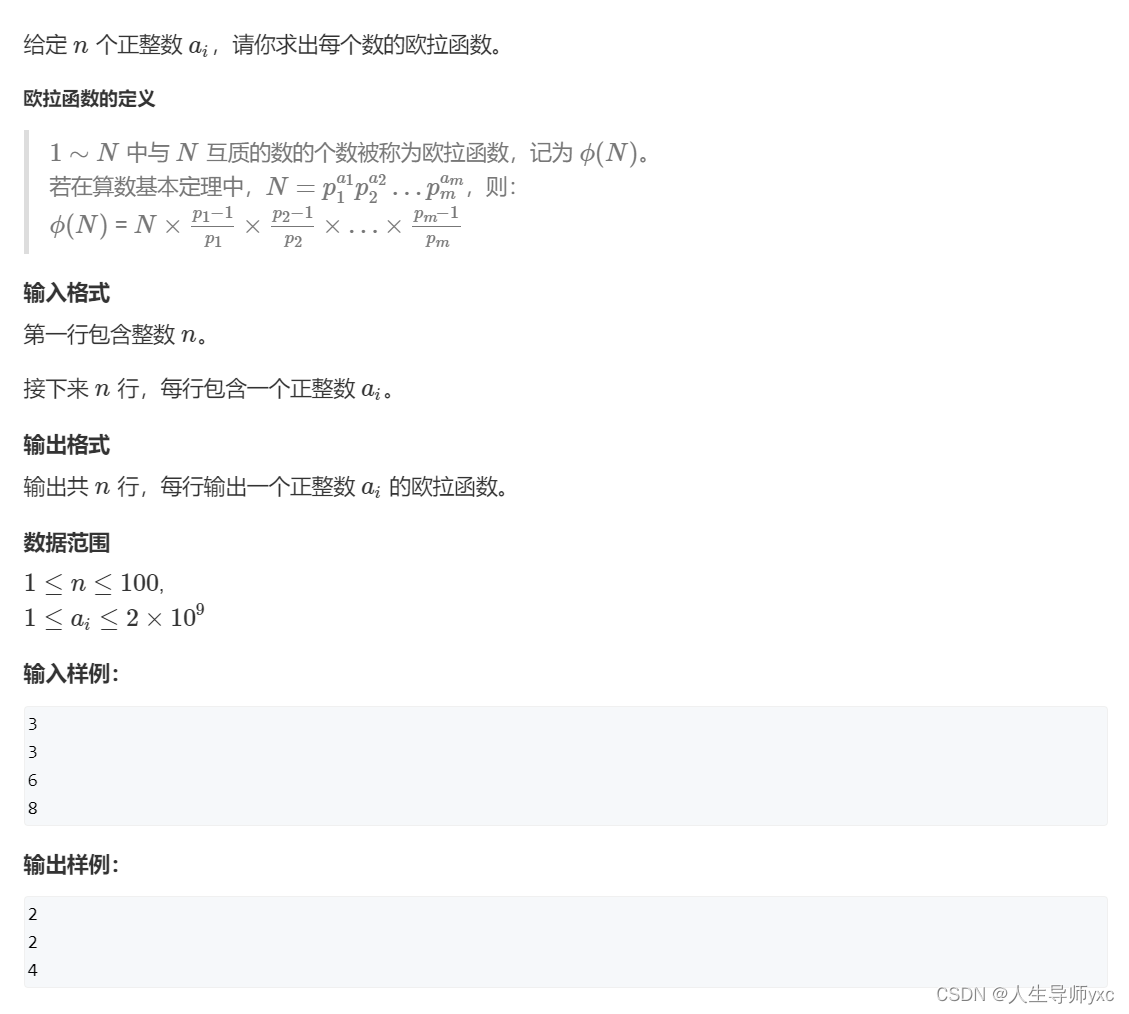
#include <iostream>
#include <algorithm>

using namespace std;

int main()
{
    int n;
    cin >> n;
    
    while (n --)
    {
        int x;
        cin >> x;
        
        long long res = x;
        for (int i = 2; i <= x / i; i ++ )
        {
            if (x % i == 0)
            {
                while (x % i == 0) x /= i;
                res = res * (i - 1) / i;
            }
        }
        if (x > 1) res = res * (x - 1) / x;
        cout << res << endl;
    }
}

模板（线性筛法）：

const int N = 1e6 + 10;
int primes[N], cnt;
bool st[N];
int phi[N];

void oula(int x)
{
    phi[1] = 1;
    for (int i = 2; i <= x; i ++)
    {
        if (!st[i])
        {
            primes[cnt ++] = i;
            phi[i] = i - 1;
        }
        for (int j = 0; primes[j] <= x / i; j ++)
        {
            st[i * primes[j]] = true;
            phi[i * primes[j]] = primes[j] * phi[i] * (primes[j] - 1) / primes[j];
            if (i % primes[j] == 0)
            {
                phi[i * primes[j]] = primes[j] * phi[i];
                break;
            } 
        }
    }
}

运用线性筛算欧拉函数思路：

Acwing874. 筛法求欧拉函数

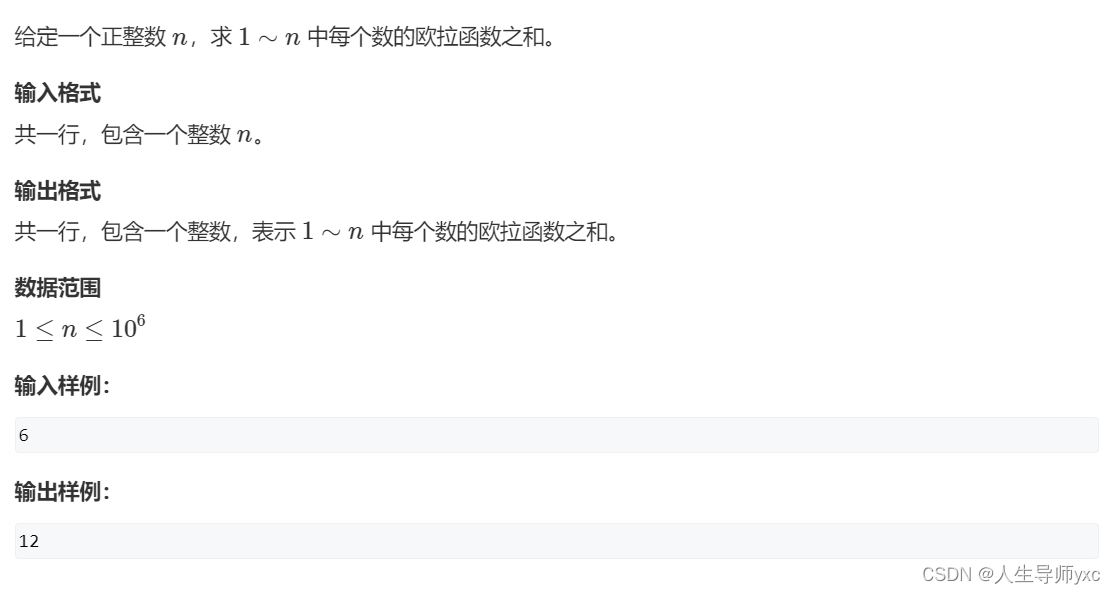
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1e6 + 10;
int primes[N], cnt;
bool st[N];
int phi[N];

void oula(int x)
{
    phi[1] = 1;
    for (int i = 2; i <= x; i ++)
    {
        if (!st[i])
        {
            primes[cnt ++] = i;
            phi[i] = i - 1;
        }
        for (int j = 0; primes[j] <= x / i; j ++)
        {
            st[i * primes[j]] = true;
            phi[i * primes[j]] = primes[j] * phi[i] * (primes[j] - 1) / primes[j];
            if (i % primes[j] == 0)
            {
                phi[i * primes[j]] = primes[j] * phi[i];
                break;
            } 
        }
    }
}
int main()
{
    int n;
    cin >> n;
   
    oula(n);
    long long res = 0;
    for (int i = 1; i <= n; i ++) res += phi[i];
    cout << res << endl;
   
}

快速幂

基本思路：

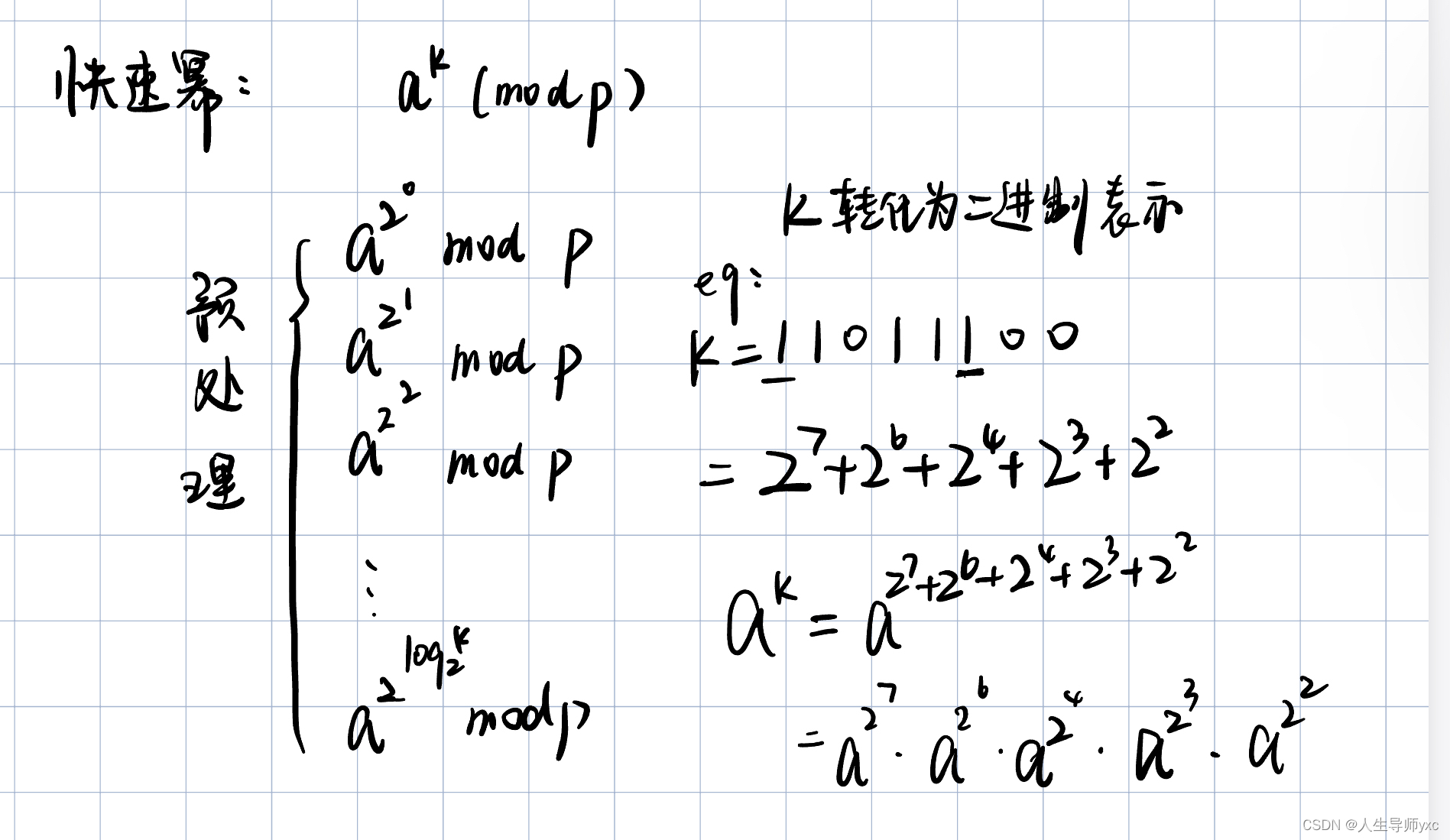
模板：

typedef long long LL;

LL qmi(int a, int k, int p)
{
    LL res = 1;
    while (k)
    {
        if (k & 1) res = res * a % p;
        k >>= 1;
        a = (LL)a * a % p;
    }
    return res;
}

AcWing 875. 快速幂

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long LL;

LL qmi(int a, int k, int p)
{
    LL res = 1;
    while (k)
    {
        if (k & 1) res = res * a % p;
        k >>= 1;
        a = (LL)a * a % p;
    }
    return res;
}
int main()
{
    int n;
    cin >> n;
    
    while (n --)
    {
        int a, k, p;
        cin >> a >> k >> p;
        cout << qmi(a, k, p) << endl;
    }
}

快速幂求逆元思路：

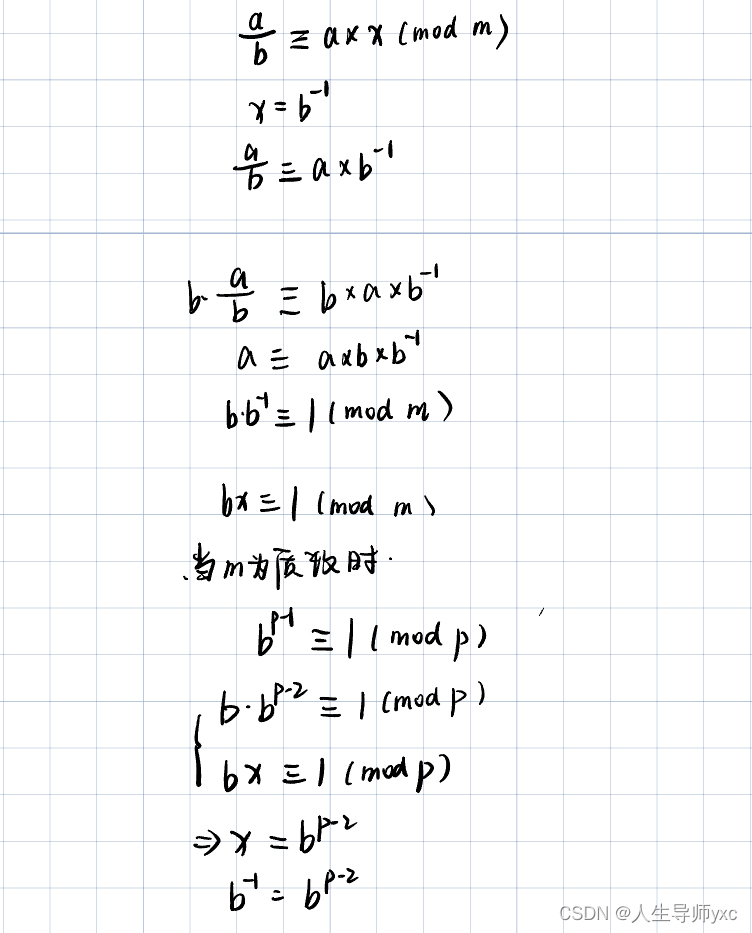AcWing 876. 快速幂求逆元

#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;

LL qmi(int a, int k, int p)
{
    LL res = 1;
    while (k)
    {
        if (k & 1) res = res * a % p;
        k >>= 1;
        a = (LL) a * a % p;
    }
    return res;
}
int main()
{
    int n;
    cin >> n;
    
    while (n --)
    {
        int a, p;
        cin >> a >> p;
        if (a % p) cout << qmi(a, p - 2, p) << endl;
        else puts("impossible");
    }
}

扩展欧几里得

基本思路：

模板：

int exgcd(int a, int b, int &x, int &y)
{
    if (b == 0)
    {
        x = 1, y = 0;
        return a;
    }
    int d = exgcd(b, a % b, y, x);
    y = y - a / b * x;
    return d;
}

Acwing877. 扩展欧几里得算法

#include <iostream>
#include <algorithm>

using namespace std;

int exgcd(int a, int b, int &x, int &y)
{
    if (b == 0)
    {
        x = 1, y = 0;
        return a;
    }
    int d = exgcd(b, a % b, y, x);
    y = y - a / b * x;
    return d;
}
int main()
{
    int n;
    cin >> n;
    while (n --)
    {
        int a, b, x, y;
        cin >> a >> b;
        exgcd(a, b, x, y);
        cout << x << ' ' << y << endl;
    }
}

裴蜀定理：

对任何整数a、b和它们的最大公约数d，关于未知数x和y的线性不定方程（称为裴蜀等式）：若a,b是整数,且gcd(a,b)=d，那么对于任意的整数x,y,ax+by都一定是d的倍数，特别地，一定存在整数x,y，使ax+by=d成立。

Acwing878. 线性同余方程

#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;
int exgcd(int a, int b, int &x, int &y)
{
    if (b == 0)
    {
        x = 1, y = 0;
        return a;
    }
    int d = exgcd(b, a % b, y, x);
    y = y - a / b * x;
    return d;
}
int main()
{
    int n;
    cin >> n;
    while (n --)
    {
        int a, b, m, x, y;
        cin >> a >> b >> m;
        int d = exgcd(a, m, x, y);
        if (b % d) puts("impossible");
        else cout << (LL)x * (b / d) % m << endl;
    }
}