💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现及文献
💥1 概述
模型预测控制(model predictive control)顾名思义有三个主要部分构成,1模型;2预测;3控制(做决策),我们只要理解这三个部分和它们之间的关系即可。
1 模型,模型可以是机理模型,也可以是一个基于数据的模型(例如用神经网络training 一个model出来)
2 预测,建立模型的目的是什么呢?建立一个模型并不是放在那里拿来看的,多半是用来做预测用的。我们每天的生活中就在不停地做建模和预测的事情,例如你过马路的时候,会预测一下是否有车能撞到你,例如我们周末想出去旅游了,可能就会去看一下天气预报。在实际生产中也有很多类似的例子,淘宝会预测每件商品未来7天的购买量,物理学家会用牛顿三大定律预测小行星的运动轨迹。
3 控制(做出决策),控制就是我需要做出动作了,在前面的例子中对应起来就是,例如你过马路的时候,会预测一下是否有车能撞到你,如果没有你就赶快过马路(控制动作)。例如淘宝会预测商品未来7天的购买量,就要看如果说有一些商品缺货了的话就赶紧去调货或者生产(控制动作),例如物理学家用牛顿三大定律预测小行星运动轨迹,如果预测到小行星会撞击到地球的话,那就提前需要采取措施来避免小行星的撞击(控制动作)。
在上面的三个例子中,第一个例子你用的是你的大脑根据以往经验学到的模型来做预测,第二个例子中可能你会用神经网络,决策树啊等等机器学习学习到的模型(说到这里可能很多童鞋会比较激动,模型预测控制可以和现在很火的人工智能 深度学习结合在一起),第三个例子中物理学家们用到的是机理模型。总之各种各样的模型都可以做预测,我们身边天天都在做预测,而预测不单单是预测的准就完事了,预测的目的是为了让我们更好的去决策。
📚2 运行结果
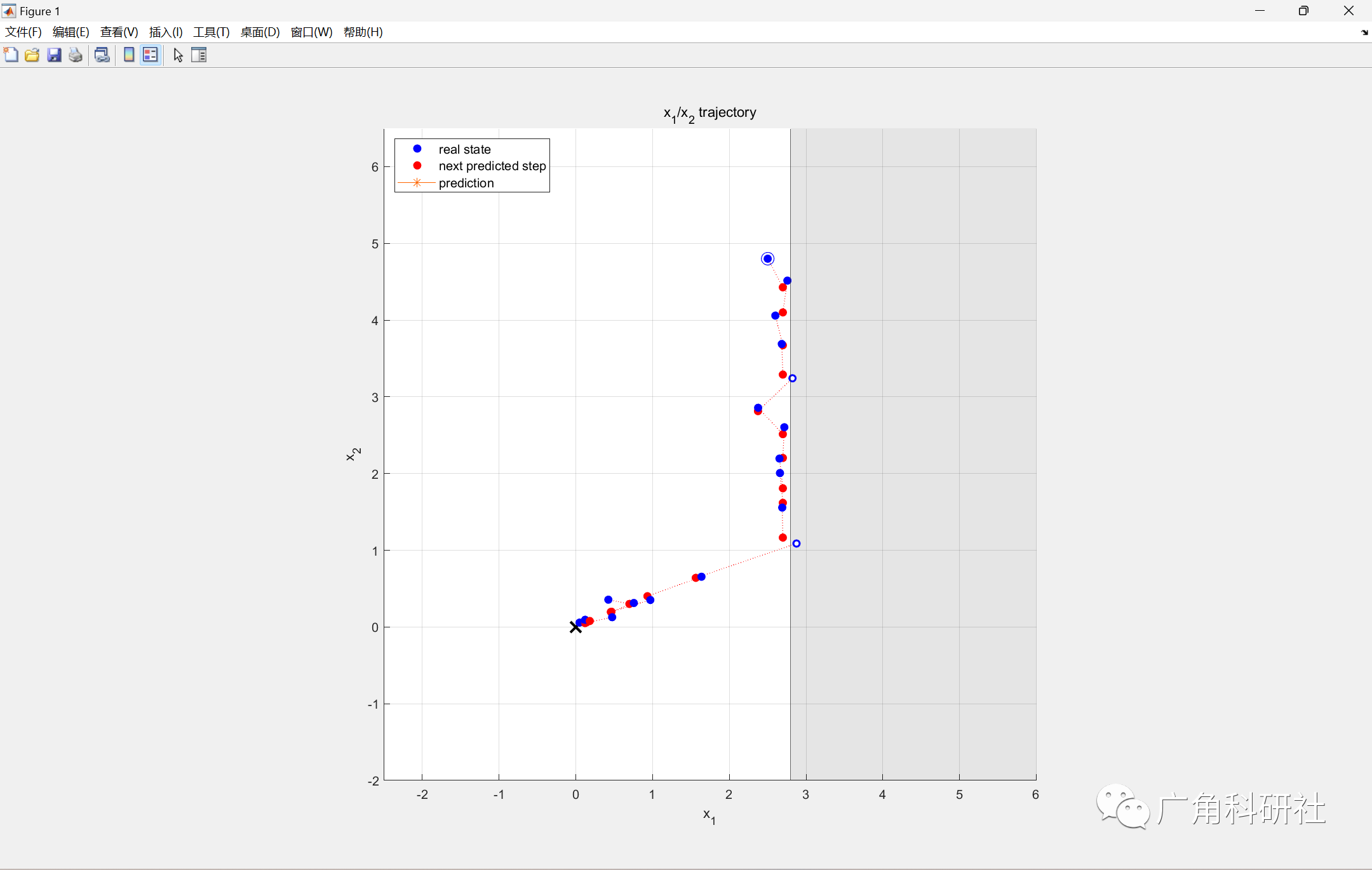
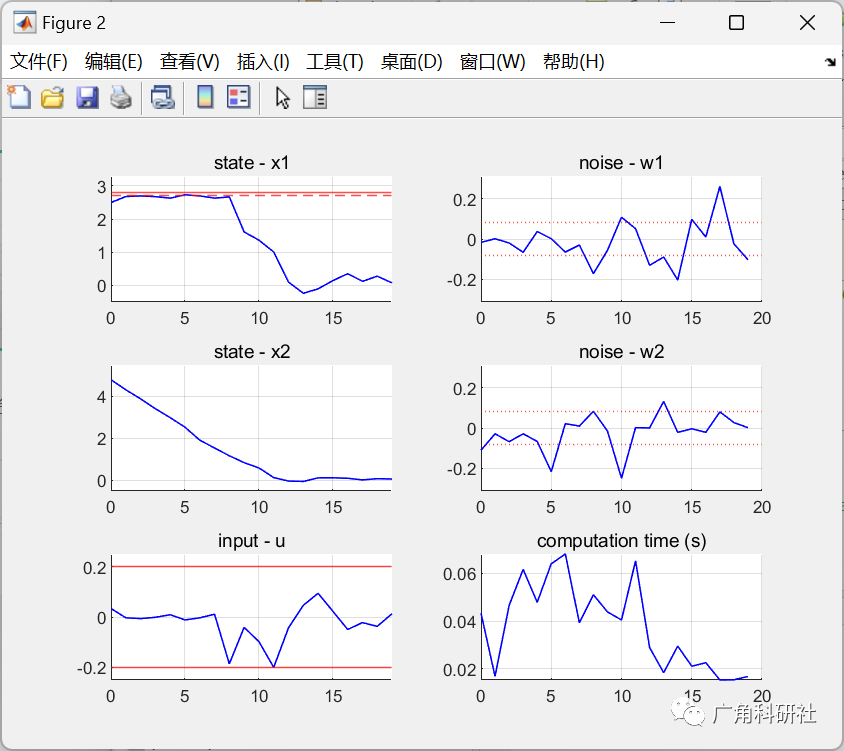
主函数部分代码:
% plot inputs and states
%% run smpc (runs new MPC simulation)
[x,u, x1_limit, sig, beta, s, comp_time]= run_mpc;
%% plot input and states
% set up figure for input and states
figure(2)
clf
plot_noise = 1; % plot noise? 0: no; 1: yes (if yes: computation time will also be plotted)
% if noise was not saved, automatically swich to 0
if exist('s','var') == 0
plot_noise = 0;
end
steps = 0:length(x)-1; % get steps (last input is computed but not applied)
% state x1
if plot_noise == 0
subplot(3,1,1)
else
subplot(3,2,1)
end
hold on
title('state - x1')
grid on
plot(steps,x(:,1), 'b', 'Linewidth',0.8)
% plot constraint only if close enough
if x1_limit < 40
yline(x1_limit, 'r', 'Linewidth',0.8)
ylim([-0.5 x1_limit+0.5]);
gamma1 = sqrt(2*[1;0]'*[sig^2 0; 0 sig^2]*[1;0])*erfinv(2*beta-1); % chance constraint addition for first predicted step
yline(x1_limit-gamma1, '
r--
', '
Linewidth
',0.8)
end
xlim([steps(1) steps(end)]);
hold off
% state x2
if plot_noise == 0
subplot(3,1,2)
else
subplot(3,2,3)
end
hold on
title('
state
- x2
')
plot(steps,x(:,2), '
b
', '
Linewidth
',0.8)
grid on
ylim([-0.5 5.5]);
xlim([steps(1) steps(end)]);
hold off
% input u
if plot_noise == 0
subplot(3,1,3)
else
subplot(3,2,5)
end
K = [0.2858 -0.4910];
u_applied = [];
for i = 1:length(u)
u_applied(i,1) = u(i,1) - K*[x(i,1); x(i,2)];
end
hold on
title('
input - u
')
grid on
plot(steps,u_applied(:,1), '
b
', '
Linewidth
',0.8)
yline(0.2,'
r
', '
Linewidth
',0.8)
yline(-0.2,'
r
', '
Linewidth
',0.8)
ylim([-0.25 0.25]);
xlim([steps(1) steps(end)]);
hold off
% plot noise (given seeding)
% rng(30,'
twister
'); % hardcoded seeding
rng(s); % retrieve seeding from run_mpc
w = [];
for i = 1: length(x)
w(i,1) = normrnd(0,sig);
w(i,2) = normrnd(0,sig);
end
🎉3 参考文献
[1]Lorenz J S,Congcong S,Gabriela C, et al. Chance-constrained stochastic MPC of Astlingen urban drainage benchmark network[J]. Control Engineering Practice,2021,115.
部分理论引用网络文献,若有侵权联系博主删除。