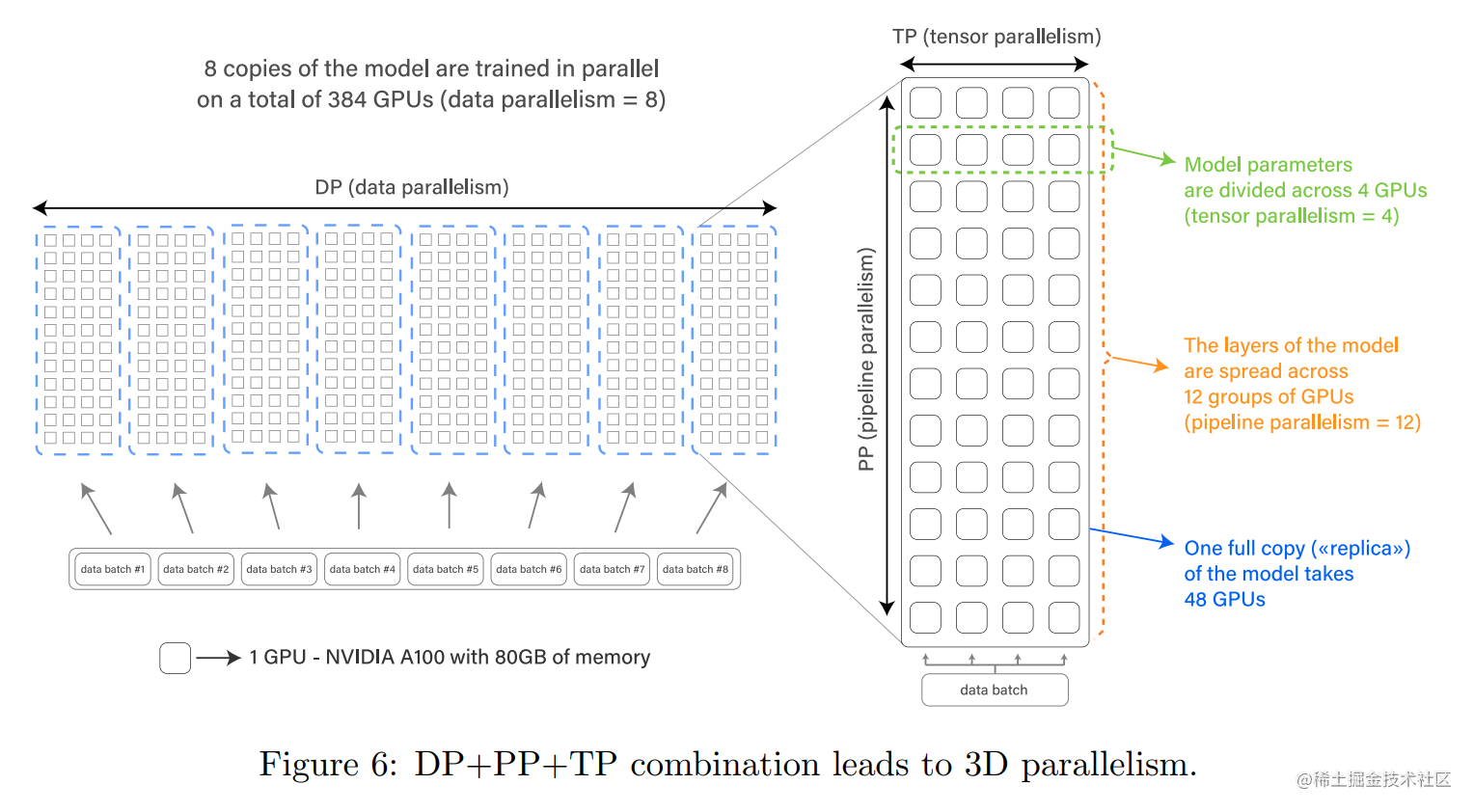
1.感知机和激活函数
感知机,是构成神经网络的基本单位,一个感知机可以接收n个输入X=(x1,x2,x3…xn)T(每个输入,可以理解为一种特征),n个输入对应n个权值W=(w1,w2,w3…wn),此外还有一个偏置项b,学过矩阵的人应该可以看出,这其实是一个y=WX+b的函数,实际上就是对所有的输入,根据权值和偏置量进行求和运算,然后作为一个神经元的输出。如下图:

通过上图可以看出,神经元里,其实是一个线性函数,我们现在先不讨论他是如何学习数据的特征,我们可以通过极限的思想,想象一下这么一个场景,要实现通过特征,进行设备分类,每个设备种类,是一个多维空间中的点,我们要做的就是用函数画出每种设备所在的多维空间中的位置,那么现在再回头看我们神经元中的这个函数,他只是一个线性函数,所以无论我们有多少个神经元和多少个网络深度,他终究在极限的边缘处,只能表示线性关系,如果想象不出来看下面的推导:

红框中就是输出层的推到公式,很明显,也是线性关系,所以为了让预测的情况更加准确,我们需要一个激活函数,把线性关系,转化为非线性关系,我们就需要把神经元设计成如下:

常见的激活函数有(科学家研究出来的): sigmoid,对数几率logistic,双曲正切Tanh,以及现在用的最多的ReLu和Leaky-ReLu,softMax。
一般分类问题,都是用softMax函数作为激活函数,因为它可以把每种输出作为概率输出

(具体的激活函数,这里不做解释了)
2.梯度下降法
梯度下降法,是我们用来计算损失函数误差,和更新w,b的常用算法,他的原理其实很简单,如下图:

假如损失函数,是一个一元2次函数,只需要随机获取2个点f(X1),f(X0)的值,进行比较,我们就可以知道大小,极小值点肯定是朝着数值小的地方,假如f(x1)<f(x0),那么就说明x1更接近极小值点,那么我们只需要朝着x1的方向,再取一个x2,慢慢的就可以向极小值靠近,这个x1和x2的距离,我们就叫步长 ,但是选择步长,是个问题,步长过小,迭代次数过多,步长过大,会产生震荡,导致在极小值点来回跳跃,所以我们就需要一个可以自动更新步长的方法,我们都知道在一个曲线的地方,这点的斜率,代表了他的抖度,当越接近极小值的时候,斜率就越小,所以用步长*这点的偏导数,就可以自动调节步长了,如果是二元函数也是一个道理,如下图:

3.BP神经网络结构

输入层:输入的其实就是数据集中的特征,一种特征代表一种输入
隐含层:就是上面说的神经元,其中隐含层的层数和神经元个数,是需要通过试验来确定的
输出层:数据集中的分类有几个,就有几个输出层神经元
在多层神经网络中,每一层的输出,代表的是上一层的输入,只要有足够多的隐含层,且每层有足够多的神经元,那么神经网络就可以拟合出任意复杂函数或空间分布,就比如下面这个:

隐含层中有三个神经元,可以看出拟合出来了三条直线,通过激活函数,就可以把线性关系转化为非线性关系。
4.损失函数:
在训练神经网络的时候,我们知道是用已经的Y和X,去训练寻找W和B,那么我们就需要知道什么情况下,W和B是已经训练的差不多了,其实就是当我们训练出来的y0和真实的y之间的差距越小,说明训练的W和B就越好,那么我们就需要定义一个损失函数,用来评估我们的模型训练质量。
这里就介绍两个常用的损失函数:
交叉熵损失函数:

均方误差函数:

5.独热编码
直接举个通俗易懂的例子,我们在训练数据的时候,有很多抽象的数据,比如设备重要程度,我们不能直接使用1,2,3来区分它的重要程度,也不能直接使用它的编码如A1,A2,A3,因为使用这些编码作为输入,计算机它理解不了,所以我们需要把他转化为欧式距离,例如设备重要程度分为,一般设备,重要设备,那么我们就应该给他们设置独热编码为[0,1],[1,0],这其实代表的是这个这两个分类到原点的欧式距离。
6.误差反向传播算法:
神经网络中,每个神经元相连接的线上都有自己的权值w和偏置量b,我们在进行一次训练后,应该根据损失函数,使用最小梯度下降法,来返回去更w和b, 然后使用更新后的w和b,再用新的数据进行训练,就这样一直重复,从而拟合出最佳的网络。

上图为一次误差反向传播的过程,隐含层和输出层使用的激活函数为softMax函数,损失函数使用的是均方误差函数,可以看到Loss函数中,它是一个带平方的函数,所以我们就可以用最小梯度下降法,来求它的下一个落脚位置,慢慢的就可以靠近loss的极小值点 ,前面我们说过,怎么求解下一个落脚点,如下图

这里只是把x和y,换成了w和b,因为x和y是我们数据集中的已知量,而w和b是我们要求的未知量,关于求w0和b0的偏导数,使用的是链式求导法则:

以上就是更新神经网络中W和B的全过程。
7.BP神经网络训练过程:
初始化网络权值和神经元的阑值,一般通过随机的方式进行初始化
前向传播:计算隐层神经元和输出层神经元的输出
后向传播:根据目标函数公式修正W和B
参考:慕课网-神经网络与深度学习(牟琦),深度学习及其应用(赵卫亮)