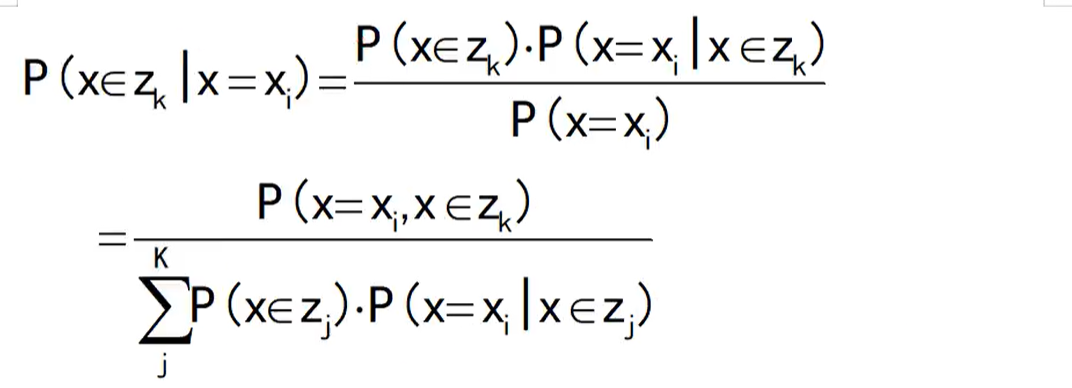GMM模型与EM算法 --> 聚类 -> 无监督机器学习[参考]
一、单个高斯分布GM的估计参数
1.1 高斯分布
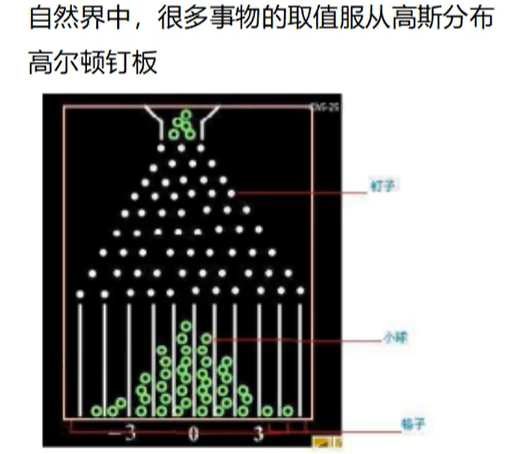
结果趋近于正态分布
每次弹珠往下走的时候,碰到钉子会随机往左还是往右走,可以观测到多次随机过程结合的

高斯分布的似然函数
X1-XN 全部发生的总概率为:
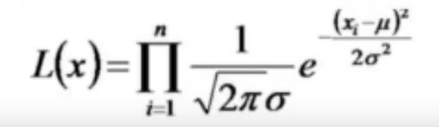


二、混合高斯模型GMM参数估计
人群中随机选出 10000 个人来,测量他们的身高男女身高虽然都服从高斯分布,但是方差均值不同假设男 N(u1,o1) 女 N(u2,o2)能否估计 u1 o1? u2 o2?
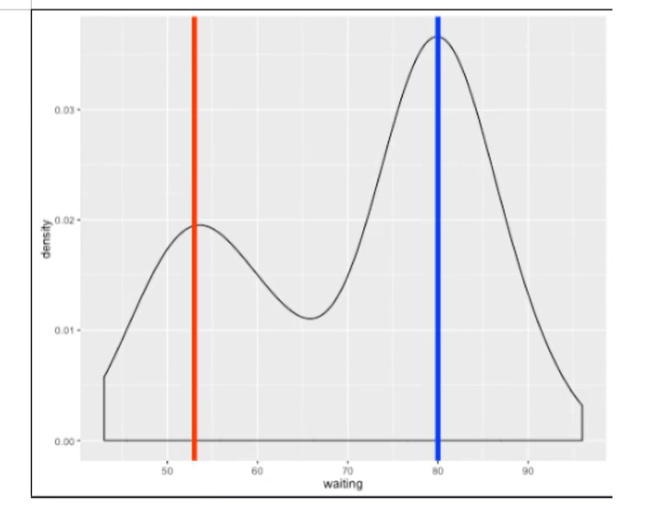
2.1 GMM混合高斯分布