文章目录
- 排序的稳定性
- 插入排序
- 插入排序的优化
- 希尔排序
- 快速排序
排序的稳定性
稳定排序:排序前2个相等的数在序列中的前后位置顺序和排序后它们2个的前后位置顺序相同。(比如:冒泡、插入、基数、归并)
非稳定排序:排序前2个数的相对位置在排序后会发生改变。(比如:选择、快速、希尔、堆等)
插入排序
插入排序,一般也被称为直接插入排序。对于少量元素的排序,它是一个有效的算法。
插入排序是一种最简单的排序方法,它的基本思想是将一个记录插入到已经排好序的有序表中,从而一个新的、记录数增1的有序表。
在其实现过程使用双层循环,外层循环对除了第一个元素之外的所有元素,内层循环对当前元素前面有序表进行待插入位置查找,并进行移动。
void Insertion_Sort(int a[], int len)
{
//外层循环 - 插入数据量
for (int i = 1; i < len; i++)
{
//内层循环 - 每一趟需要做的事情
for (int j = i - 1; j > -1; j--)
{
if (a[j]>a[j + 1])
{
int temp = a[j];
a[j] = a[j + 1];
a[j + 1] = temp;
}
}
}
}
插入排序的优化
在下面函数中,通过使用一个临时变量temp来保存当前需要插入的元素。外层循环通过对整个待排序序列进行遍历,从第二个元素开始(下标为1),将当前元素保存在temp中。
然后,内层循环从当前元素的前一个元素开始向前遍历,直到找到合适的位置插入temp。在内层循环中,如果当前遍历到的元素大于temp,就将该元素后移一位,给temp腾出位置。
内层循环结束后,将temp插入到合适的位置,即将其赋值给a[j+1],这样就完成了一次元素的插入。
通过这种方式,不断地将元素逐个地插入到已排序的序列中,最终得到一个完全有序的序列。
void Insertion_Sort(int a[], int len)
{
int temp, i, j;
//外层循环 - 插入数据量
for (i = 1; i < len; i++)
{
temp = a[i];
//内层循环 - 每一趟需要做的事情
for (j = i - 1; j > -1 && a[j] > temp; j--)
{
a[j + 1] = a[j];
}
//移动结束
a[j + 1] = temp;
}
}
希尔排序
希尔排序(Shell Sort)是一种改进的插入排序算法,也被称为“缩小增量排序”(Diminishing Increment Sort)。希尔排序通过将待排序序列分割成多个子序列来进行排序,最终将这些子序列逐步合并为一个有序序列。
希尔排序的核心思想是通过定义一个增量序列(也称为间隔序列),将待排序序列划分成若干个子序列,并对这些子序列分别进行插入排序。随着排序的进行,增量序列会不断减小,直到变为1,此时对整个序列进行一次插入排序,最终完成排序。
希尔排序的步骤如下:
-
首先确定一个增量序列,一般选择初始增量为序列长度的一半,然后每次将增量折半,直到增量变为1。
-
对每个增量进行插入排序,即将待排序序列划分成若干个子序列,对每个子序列进行插入排序。
-
在每次插入排序中,按照增量的大小,将元素分组,对每组进行插入排序。
-
不断缩小增量,重复步骤2和步骤3,直到增量为1,进行最后一次插入排序,完成排序。
举个例子:
- 如下图所示,现有一序列:8、5、7、3、6、1、2、8,选择初始增量为序列长度的一般,即初始增量为4(分为四个组,标红数字所示)。

- 第一次交换(组别增量为4)
- 8和6为一组,5和1为一组……,队每组中的数比较排序,(例:第一组排序,8比6大,则8、6互换位置,以此类推)排序后的结果如下图所示。

- 8和6为一组,5和1为一组……,队每组中的数比较排序,(例:第一组排序,8比6大,则8、6互换位置,以此类推)排序后的结果如下图所示。
- 第二次交换(组别增量由4变为2)如下图所示。

- 先对1组进行比较,首先6作为已序。
- 第一次比较:1组的第一个数(6)与第二个数(2)进行比较,2<6小,插入到6的位置,6换到2的位置。
- 第二次比较:1组的第二个数(6)与第三个数(8)进行比较,6<8,则不进行插入。
- 第三次比较:1组的第三个数(8)与第4个数(7)进行比较,8>7,所以7插入到8的位置,8换到7的位置。
- 最终1组排序的结果如下:

- 同理,对2组进行比较后的结果如下图所示。

- 第三次交换(组别增量从2变为1)

- 组别增量变为1之后,对整体做插入排序,结果如下。

- 组别增量变为1之后,对整体做插入排序,结果如下。
希尔排序函数:
//希尔排序
void Shell_Sort(int a[], int len)
{
int temp, i, j, n = 0;
//增量分组
int jump = len >> 1;
while (jump != 0)
{
//外层循环 - 插入数据量
for (i = jump; i < len; i++)
{
temp = a[i];
//内层循环
for (j = i - jump; j >= 0 && a[j]>temp; j -= jump)
{
a[j + jump] = a[j];
n += 1;
}
//移动结束
a[j + jump] = temp;
}
//增量更新
jump >>= 1;
}
}
分别在优化后的插入排序函数和希尔排序中定义一个变量n,用来统计各自进行数据交换的次数,结果如下:
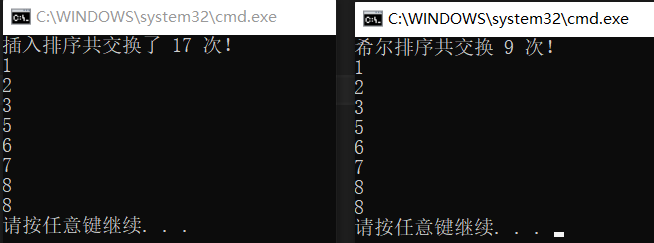
插入排序交换的次数约是希尔排序交换次数的两倍!
快速排序
快速排序(Quicksort)是对冒泡排序的一种改进。
快速排序的核心思想是通过分治法将一个大的待排序序列逐步地分割成小的子序列,然后对这些子序列进行排序,最终得到一个有序序列。具体步骤如下:
- 选择一个基准元素(pivot),可以是序列中的任意一个元素。
- 将序列分为两部分,小于等于基准元素的部分和大于基准元素的部分。可以通过两个指针 i 和 j 来实现,开始时 i 指向序列的第一个元素,j 指向序列的最后一个元素。
- 从左向右找出第一个大于基准元素的元素,记为 a。
- 从右向左找出第一个小于等于基准元素的元素,记为 b。
- 如果 i < j,则交换 a 和 b 的位置,然后继续找下一对 a 和 b。
- 如果 i >= j,则停止查找。
- 将基准元素与 j 所指向的元素交换位置,即将基准元素放在合适的位置。
- 递归地对基准元素左边和右边的子序列进行快速排序。
以下是一个使用 C 语言实现的快速排序代码示例:
#include <stdio.h>
// 交换两个元素的值
void swap(int *a, int *b) {
int temp = *a;
*a = *b;
*b = temp;
}
// 快速排序的递归函数
void quickSort(int arr[], int low, int high)
{
if (low < high)
{
int pivot = arr[low]; // 选择第一个元素作为基准元素
int i = low, j = high;
while (i < j)
{
while (i < j && arr[j] > pivot)
{
j--;
}
while (i < j && arr[i] <= pivot)
{
i++;
}
if (i < j)
{
swap(&arr[i], &arr[j]);
}
}
swap(&arr[low], &arr[i]);
quickSort(arr, low, i - 1); // 对左边子序列进行快速排序
quickSort(arr, i + 1, high); // 对右边子序列进行快速排序
}
}
// 打印数组元素
void printArray(int arr[], int size)
{
for (int i = 0; i < size; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
}
int main()
{
int arr[] = {8, 5, 7, 3, 6, 1, 2, 8};
int size = sizeof(arr) / sizeof(arr[0]);
printf("原始数组:");
printArray(arr, size);
quickSort(arr, 0, size - 1);
printf("排序后数组:");
printArray(arr, size);
return 0;
}
输出结果:
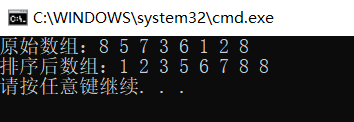
分析程序:
代码首先定义了一个 swap 函数用于交换两个元素的值。然后,quickSort 函数使用递归实现了快速排序的具体操作。最后,在 main 函数中创建一个待排序的数组,并调用 quickSort 函数对数组进行排序。最终,通过调用 printArray 函数打印排序后的数组。