动态规划的解题步骤可以分为以下五步,大家先好好记住
1.创建dp数组以及明确dp数组下标的含义 2.制定递推公式 3.初始化 4.遍历顺序 5.验证结果
股票购买时机问题的解题核心思路
当天的收益是根据前一天持有股票还是不持有股票的状态决定的
那么很自然的我们就想到了使用动态规划的思想来解决问题,接下来就根据动态规划以及解题的核心思想来解决 股票购买时机问题
121. 买卖股票的最佳时机
根据题意: 某一天 买入这只股票,并选择在 未来的某一个不同的日子
也就是说我们只用买卖股票一次即可 那么根据动态规划的解题步骤以及核心思想我们一步步分析
1.创建dp数组以及明确dp数组下标的含义
//0 表示持不有股票的状态 1表示持有股票的状态
int[][] dp = new int[prices.length][2];2.制定递推公式
//持有的状态 - 要么是保持持有状态 要么是今天买入股票
dp[i][0] = Math.max(dp[i-1][0],-prices[i]);
//不持有的状态 - 要么是保持不持有状态 要么是今天卖出股票
dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0] + prices[i]);3.初始化
dp[0][0] = -prices[0];
dp[0][1] = 0;4.遍历顺序
//从前往后遍历- 由于我们是从 i = 1 开始遍历的所以是prices[i-1]
for(int i = 1;i < dp.length;i++){
//持有
dp[i][0] = Math.max(dp[i-1][0],-prices[i]);
//不持有
dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0] + prices[i]);
}5.验证
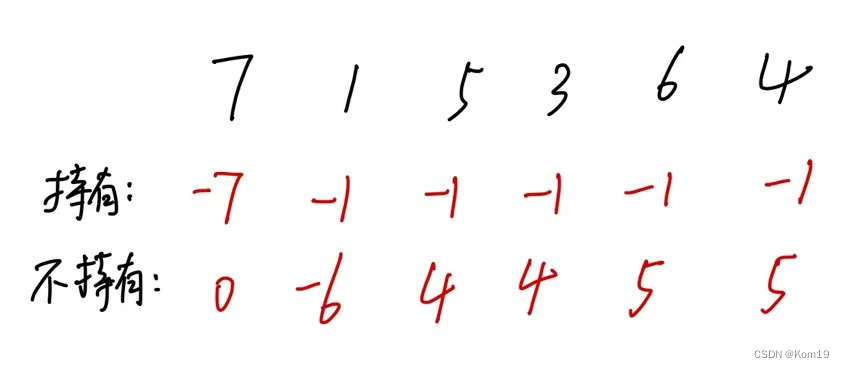
最后贴上完整代码
public int maxProfit(int[] prices) {
int len = prices.length;
//dp数组下标的含义是当日持有股票和不持有股票的最大利润
int[][] dp = new int[len][2];
//递推公式
//dp[i][0] 表示持有股票 dp[i][1] 表示不持有股票
//dp[i][0] = Math.max(dp[i-1][0],dp[i-1][0] - prices[i]);
//dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0] + prices[i]);
//初始化
dp[0][0] = -prices[0];
dp[0][1] = 0;
for(int i = 1;i < dp.length;i++){
//持有
dp[i][0] = Math.max(dp[i-1][0],-prices[i]);
//不持有
dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0] + prices[i]);
}
return Math.max(dp[len-1][0],dp[len-1][1]);
}122. 买卖股票的最佳时机 II
本题遇上一题最大的不同就是可以多次买卖股票了,大题思路和上一题是差不多的
所以我们只需要在 2.指定递推公式 这里修改一下即可
由于可以多次买卖股票了,那么在今天买入股票这个步骤就需要参考昨天不持有股票的状态了
这就是和上一题不同的地方,上一题由于只需要买入一次,所以不用参考任何状态
那么只需要简单的进行修改即可
for(int i = 1;i < dp.length;i++){
//持有
dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1] - prices[i]);
//不持有
dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0] + prices[i]);
}123. 买卖股票的最佳时机 III
本题说了只能购买两次股票那么难度就增加了,但是核心思路“当天的收益是根据是前一天持有股票还是不持有股票的状态决定的”还是不变的
1.创建dp数组以及明确dp数组下标的含义
int len = prices.length;
//dp数组的下标的含义是当日持有股票或者不持有股票获得的最大收益
//0~1表示第一次持有股票 2~3表示第二次持有股票
int[][] dp = new int[len + 1][4];2.制定递推公式
第一次持有是第一题的递推公式思路(只能买卖股票一次)
第二次持有是第二题的思路,因为此时买卖股票需要结合上一次买卖股票的状态来决定(多次买卖股票)
结合上两题的思想我们得到递推公式
//第一次持有
dp[i][0] = Math.max(dp[i-1][0], -prices[i]);
//第一次不持有
dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0] + prices[i]);
//第二次持有
dp[i][2] = Math.max(dp[i-1][2],dp[i-1][1] - prices[i]);
//第二次不持有
dp[i][3] = Math.max(dp[i-1][3],dp[i-1][2] + prices[i]);3.初始化
//第一次持有
dp[0][0] = -prices[0];
//第一次不持有
dp[0][1] = 0;
//第二次持有
dp[0][2] = -prices[0];
//第二次不持有
dp[0][3] = 0;4.遍历顺序
从前往后
for(int i = 1;i < dp.length;i++){
dp[i][0] = Math.max(dp[i-1][0], -prices[i-1]);
dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0] + prices[i]);
dp[i][2] = Math.max(dp[i-1][2],dp[i-1][1] - prices[i]);
dp[i][3] = Math.max(dp[i-1][3],dp[i-1][2] + prices[i]);
}最后完整代码如下
public int maxProfit(int[] prices) {
int len = prices.length;
int[][] dp = new int[len][4];
//第一次持有
dp[0][0] = -prices[0];
//第一次不持有
dp[0][1] = 0;
//第二次持有
dp[0][2] = -prices[0];
//第二次不持有
dp[0][3] = 0;
for(int i = 1;i < dp.length;i++){
dp[i][0] = Math.max(dp[i-1][0], -prices[i]);
dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0] + prices[i]);
dp[i][2] = Math.max(dp[i-1][2],dp[i-1][1] - prices[i]);
dp[i][3] = Math.max(dp[i-1][3],dp[i-1][2] + prices[i]);
}
return dp[len-1][3];
}188. 买卖股票的最佳时机 IV
别被吓着!这题实际上和上一题是一模一样的!
区别就在于这一题是购买K次,而K则是题目随机分配的
但思路还是一样的!
那么怎么来解决掉0~K次的各个状态呢?答案也很简单!使用for循环
比如初始化的时候我们可以使用for循环来进行初始化
//初始化
for(int i = 1;i < k*2 + 1;i += 2){
//规定奇数是持有的状态 偶数是不持有的状态
dp[0][i] = -prices[0];
}当我们制定递推公式的时候也是使用for循环来帮助我们实现的
//遍历顺序
for(int i = 1;i < len;i++){
for(int j = 0;j < 2*k - 1;j += 2){
//持有
dp[i][j+1] = Math.max(dp[i-1][j+1],dp[i-1][j] - prices[i]);
//不持有
dp[i][j+2] = Math.max(dp[i-1][j+2],dp[i-1][j+1] + prices[i]);
}
}你们看完可能会觉得很疑惑:不是说第一次持有股票不需要参考任何状态吗?那这个代码怎么解释
dp[i - 1][j] - prices[i];
注意我们在初始化的时候是从 i = 1 开始的 也就是说 第一次持有股票时的状态还是
dp[i][0] = - prices[i];
这样大家应该明白了吧
最后贴上完整的代码
class Solution {
public int maxProfit(int k, int[] prices) {
int len = prices.length;
//dp数组
int[][] dp = new int[len][k*2 + 1];
//递推公式
//持有操作 奇数
//dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j] - price[i]);
//不持有操作 偶数
//dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j] + price[i]);
//初始化
for(int i = 1;i < k*2 + 1;i += 2){
dp[0][i] = -prices[0];
}
//遍历顺序
for(int i = 1;i < len;i++){
for(int j = 0;j < 2*k - 1;j += 2){
//持有
dp[i][j+1] = Math.max(dp[i-1][j+1],dp[i-1][j] - prices[i]);
//不持有
dp[i][j+2] = Math.max(dp[i-1][j+2],dp[i-1][j+1] + prices[i]);
}
}
//验证
return dp[len - 1][k*2];
}
}309. 买卖股票的最佳时机含冷冻期(老实说,这题是我觉得股票买卖时机里面最难的一题...)
想要解决这道难题首先我们得分析好状态,不然会越来越懵逼的
首先由持有状态 不持有状态(保持不持有状态,前一天是冷冻期状态) 冷冻期状态
我们先定义好dp数组
int[][] dp = new int[len][4];
//1.持有股票(保持持有股票/今天买入股票) 2.保持不持有股票 3.今天卖出股票 4.处于冷冻期
//持有
dp[0][0] = -prices[0];
//不持有
dp[0][1] = 0;
//今天卖出股票
dp[0][2] = 0;
//处于冷冻期 = 昨天卖出股票
dp[0][3] = dp[0][2];持有状态可以由不持有状态和冷冻期状态进行推导,它可以是保持持有状态也可以是今天买入
dp[i][0] = Math.max(Math.max(dp[i-1][1],dp[i-1][3]) - prices[i],dp[i-1][0]);那么不持有状态可以由保持不持有状态和前一天是冷冻期进行推导
dp[i][1] = Math.max(dp[i-1][1],dp[i-1][3]);今天卖出股票直接由持有状态进行推导
dp[i][2] = dp[i-1][0] + prices[i];冷冻期状态实际上就是保持了昨天卖出股票的状态
dp[i][3] = dp[i-1][2];状态推导完了剩下也就简单了,直接上代码
class Solution {
public int maxProfit(int[] prices) {
int len = prices.length;
int[][] dp = new int[len][4];
//1.持有股票(保持持有股票/今天买入股票) 2.保持不持有股票 3.今天卖出股票 4.处于冷冻期
//持有
dp[0][0] = -prices[0];
//不持有
dp[0][1] = 0;
//今天卖出股票
dp[0][2] = 0;
//处于冷冻期 = 昨天卖出股票
dp[0][3] = dp[0][2];
for(int i = 1;i < len;i++){
//持有股票
dp[i][0] = Math.max(Math.max(dp[i-1][1],dp[i-1][3]) - prices[i],dp[i-1][0]);
//保持不持有股票
dp[i][1] = Math.max(dp[i-1][1],dp[i-1][3]);
//今天卖出股票
dp[i][2] = dp[i-1][0] + prices[i];
//处于冷冻期
dp[i][3] = dp[i-1][2];
}
return Math.max(dp[len-1][1],Math.max(dp[len-1][2],dp[len-1][3]));
}
}714. 买卖股票的最佳时机含手续费
本题实际上只用在第二题的基础上扣除手续费就好了只需要修改这一段代码即可
dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0] + prices[i] - fee);股票买卖时机问题我们只需要把握一点就是把 持有和不持有 两个状态分析好,题目就会变得很简单