【LeetCode刷题（数据结构）】：翻转二叉树

news2024/11/22 16:05:08

在这里插入图片描述

方法一：递归

思路与算法
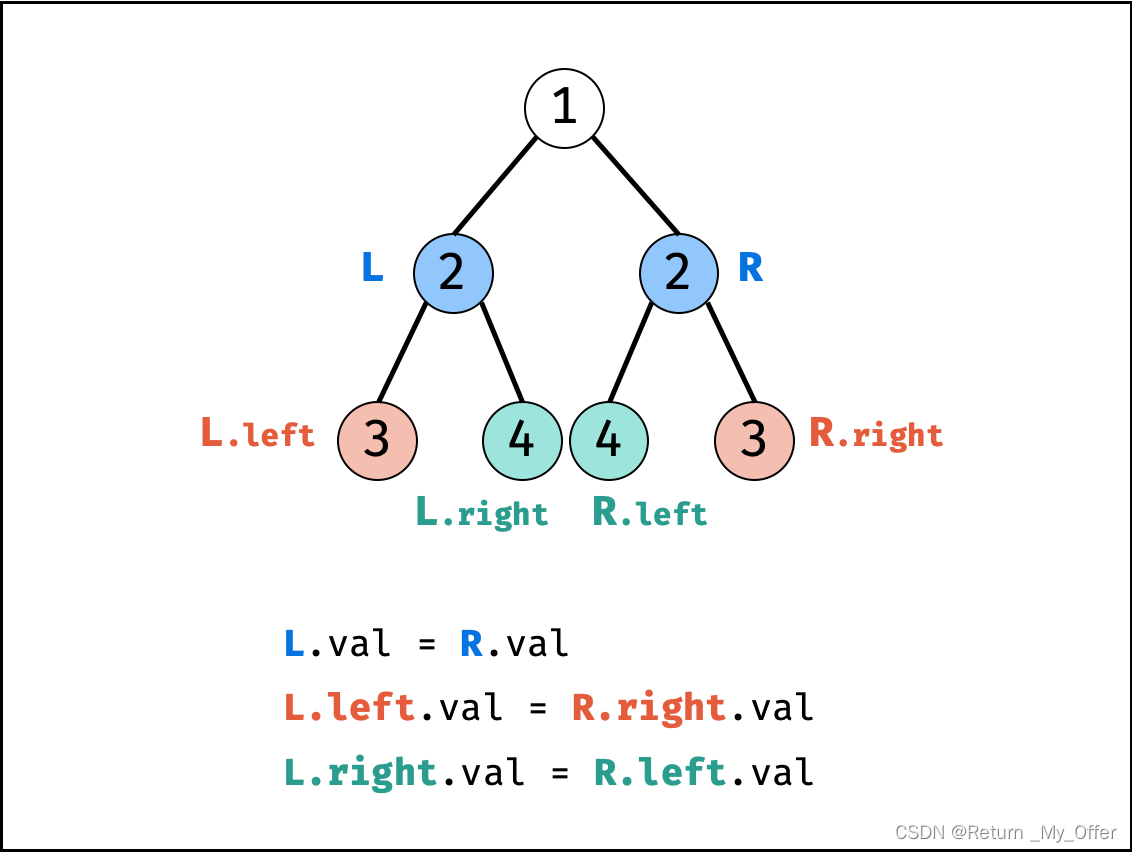
这是一道很经典的二叉树问题。显然，我们从根节点开始，递归地对树进行遍历，并从叶子节点先开始翻转。如果当前遍历到的节点 root\textit{root}root 的左右两棵子树都已经翻转，那么我们只需要交换两棵子树的位置，即可完成以 root\textit{root}root 为根节点的整棵子树的翻转
代码

struct TreeNode* invertTree(struct TreeNode* root) {
    if (root == NULL) {
        return NULL;
    }
    struct TreeNode* left = invertTree(root->left);
    struct TreeNode* right = invertTree(root->right);
    root->left = right;
    root->right = left;
    return root;
}

复杂度分析

时间复杂度：O(N) 其中 NNN 为二叉树节点的数目。我们会遍历二叉树中的每一个节点，对每个节点而言，我们在常数时间内交换其两棵子树
空间复杂度：O(N) 使用的空间由递归栈的深度决定，它等于当前节点在二叉树中的高度。在平均情况下，二叉树的高度与节点个数为对数关系，即 O(log⁡N)而在最坏情况下，树形成链状，空间复杂度为 O(N)
在这里插入图片描述

其实就是交换一下左右节点，然后再递归的交换左节点，右节点根据动画图我们可以总结出递归的两个条件如下
终止条件：当前节点为 null 时返回
交换当前节点的左右节点，再递归的交换当前节点的左节点，递归的交换当前节点的右节点

2 迭代

在这里插入图片描述

struct TreeNode* invertTree(struct TreeNode* root){
    if(root == NULL) return NULL;
    struct TreeNode* stack[1000];
    int top = -1;
    stack[++top] = root;
    while(top >= 0){
        struct TreeNode* node = stack[top--];
        struct TreeNode* temp = node->left;
        node->left = node->right;
        node->right = temp;
        if(node->left != NULL) stack[++top] = node->left;
        if(node->right != NULL) stack[++top] = node->right;
    }
    return root;
}