问题

今天在做23李六第二套的时候看到了一道题：

答案里面说的直接再加一个y=y和上面的两个方程就凑成了三个方程（x关于y的，y关于y的，z关于y的，最后每个方程都对y求导，再代入y=1，就有了方向向量）。这里我产生了一个疑问，参数式这么任意的吗？我记得只有t才能做参数，还有就是标准的参数式应该是如下的吧，怎么可以不带入点呢？以及为什么对参数求导就能得到方向向量呢？

思考

因此，我就开始疑惑参数式的本质究竟是什么。

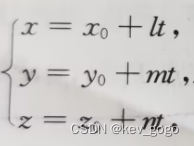
显然，在这里，x对t求导对应的是l，是方向向量和x轴的夹角的k倍，也就是cosα，相应的，m是和y轴夹角的k倍，n是和z轴夹角的k倍（三个k相等），单位化后就有：
(l,m,n)->(cosα,cosβ,cosγ)

这个cosα具体等于什么呢？
比如方向向量是（l,m,n)那么（l，m，n）点乘（1，0，0）=|（l，m，n，）||（1，0，0）|cosα，即方向向量点乘坐标轴向量（cosα对应和x轴的夹角），cosα就是l除以l的模，因此，cosα和l是有线性关系的，方向向量单位化后就变成了cos的形式。这也是为什么三个cos的模为1（因为平方相加就变成了模除以模）

发现一个有用的hhh，向量点乘可以凑出来向量之间的夹角。

那么直线式子的看的更清晰了，不过这只是说，如果我们有了方向向量，可以去列参数式，但是没有方向向量的时候，我们如何通过参数式构造方向向量？

我想，答案只能是随便构建了。。。只要能将x,y,z通过同一个参数表示（比如t，那么就大功告成（这个t可以是y或者x等等）），然后x，y，z分别对t求导即可得出方向向量。。。

虎头蛇尾了，但是真的没想出来，咋能求出来方向向量（就是这个的物理意义是什么）有机会再搞吧。。。