前言
众所周知计算机模拟的随机是伪随机,但在结果看来依然和现实中的随机差别不大。
例如掷硬币,连续掷很多很多次之后,总有连续七八十来次同一个面朝上的情况出现,计算机中一般的随机函数也能很好模拟这一点。
但在游戏中,假如有一个50%概率会出现的情况,经常连续七八十来次不出现,这样其实非常影响游戏体验。
那么为了增加这部分游戏体验,我们如何避免上述情况发生,使某个概率能在总体上较为均匀地分布呢?
例如现在有这样的需求:
A. 暴击率总体为20%
B. 要求每十次攻击,至少有一次暴击
C. 要求暴击的总体分布较为均匀
算法预览
经过一段时间的深思熟虑,笔者终于构建了一种名为“动态平衡概率”的算法。
虽然它还有一些局限性,但已经达到了基本可用的状态。
先上代码,为了方便演示图表,这里就用 python 了:
import matplotlib.pyplot as plt
import random
# 初始化变量
InitCritPercent = 0.2 # 初始暴击率
dynamicCritPercent = 0.2 # 动态暴击率
currentCritPercent = 0 # 当前暴击概率
deltaCritPercent = 0 # 当前暴击率与初始暴击率的差值(用来表示变化)
attackTotalCount = 0 # 总攻击次数
critTotalCount = 0 # 总暴击次数
noCritStreakCount = 0 # 连续未暴击次数
# 给 plot 准备的列表
currentCritPercentList = []
deltaCritPercentList = []
dynamicCritPercentList = []
noCritStreakCountList = []
isCriticalList = []
# 获取最佳的 N
def find_optimal_N(p):
one_minus_p = 1 - p
for i in range(1, 501):
if one_minus_p ** i <= 0.05:
return i
return 500 # 如果未找到合适的 N,则默认返回 500
# 测试 10000 次
for i in range(10000):
# 核心代码 ↓
attackTotalCount += 1
isCritical = False
# 检查当前攻击数是否大于 0
if attackTotalCount > 0:
# 计算当前暴击概率
currentCritPercent = critTotalCount / attackTotalCount
# 计算当前暴击概率与初始暴击率的差值
deltaCritPercent = abs(InitCritPercent - currentCritPercent)
# 计算动态暴击率
dynamicCritPercent = (attackTotalCount * (InitCritPercent - currentCritPercent) + currentCritPercent) * pow(deltaCritPercent, 0.5)
# 检查是否连续 N - 1 次未暴击
if noCritStreakCount < find_optimal_N(InitCritPercent) - 1:
percent = random.random()
if percent <= dynamicCritPercent:
isCritical = True
noCritStreakCount = 0
else:
noCritStreakCount += 1
else:
isCritical = True
noCritStreakCount = 0
if isCritical:
critTotalCount += 1
# 核心代码 ↑
# 将数据添加到列表中
currentCritPercentList.append(currentCritPercent)
deltaCritPercentList.append(deltaCritPercent)
dynamicCritPercentList.append(dynamicCritPercent)
noCritStreakCountList.append(noCritStreakCount)
isCriticalList.append(int(isCritical))
# 创建多表格
fig, axs = plt.subplots(2)
# 每 100 条数据标注一下
for i in range(0, len(currentCritPercentList), 100):
axs[0].annotate(f"{currentCritPercentList[i]:.3f}", (i, currentCritPercentList[i]))
# 画出暴击概率数据表格
axs[0].plot(currentCritPercentList, label='Current Crit Percent', color='r')
axs[0].plot(deltaCritPercentList, label='Delta Crit Percent', color='g')
axs[0].plot(dynamicCritPercentList, label='Dynamic Crit Percent', color='b')
axs[0].set_xlabel('Total Attacks')
axs[0].set_ylabel('Probability')
axs[0].legend()
# 画出连续未暴击次数的表格
axs[1].plot(noCritStreakCountList, label='No-Crit Streak', color='m')
axs[1].plot(isCriticalList, label='Is Critical', color='c')
axs[1].set_xlabel('Total Attacks')
axs[1].set_ylabel('No-Crit Streak / Is Critical')
axs[1].legend()
plt.show()
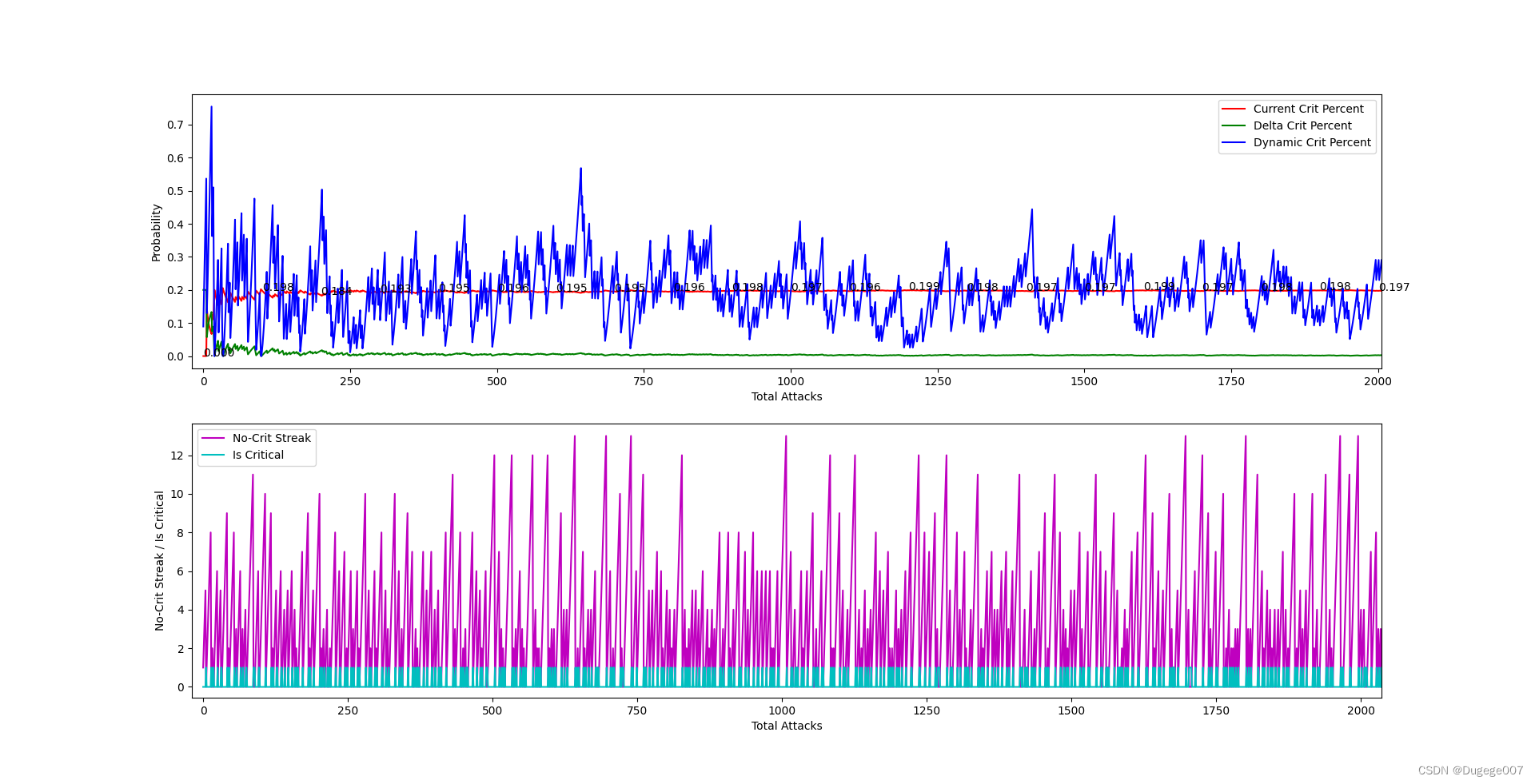
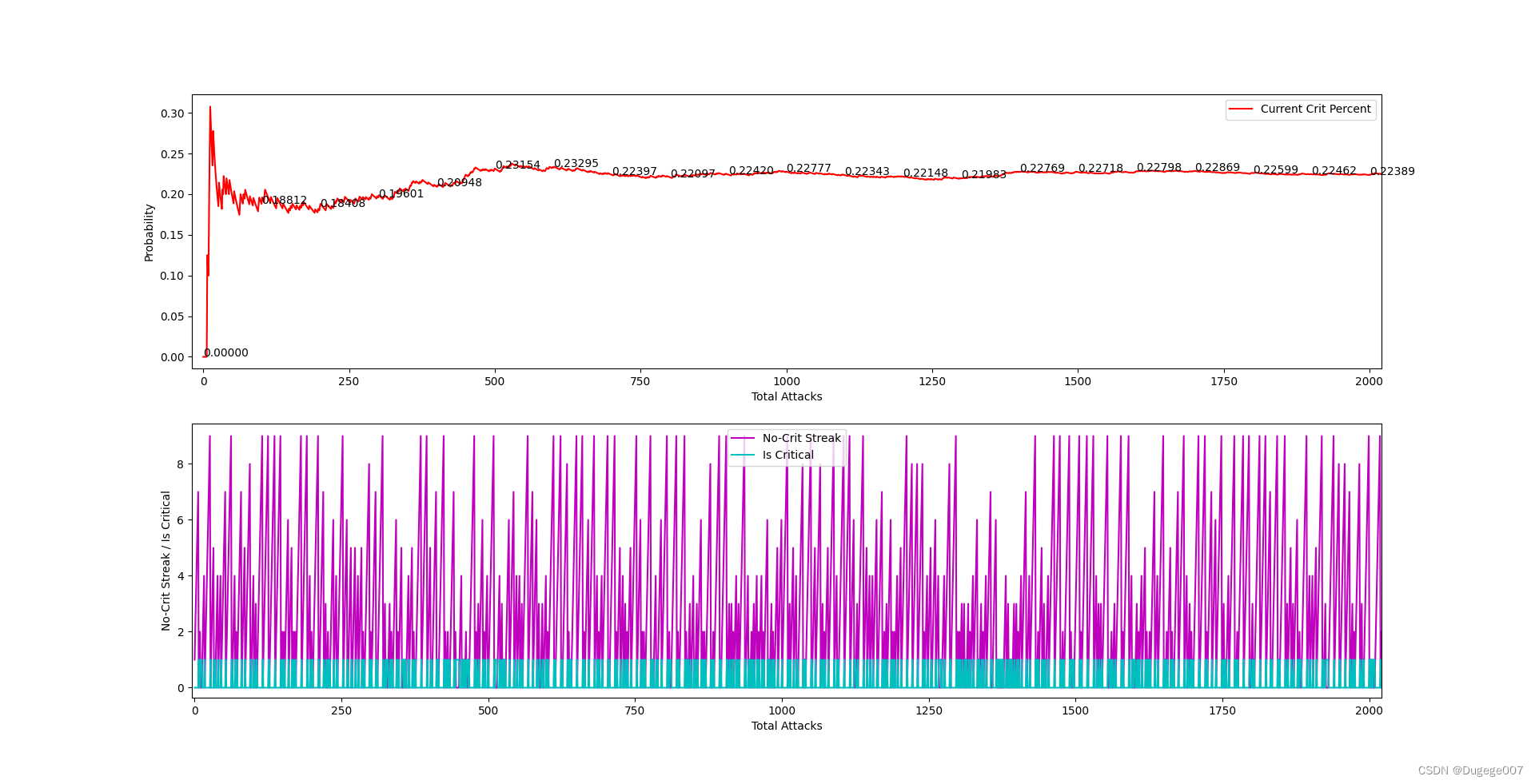
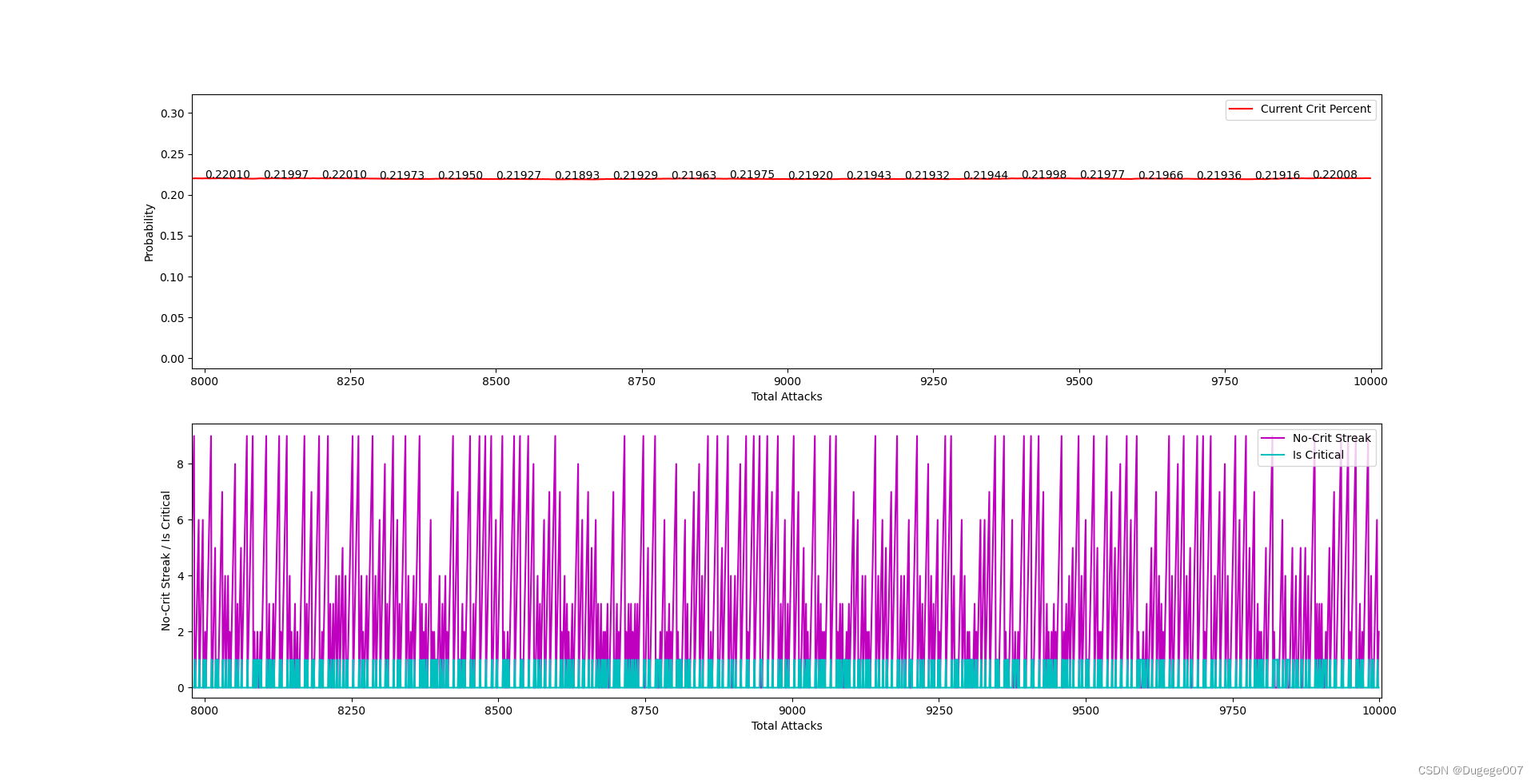
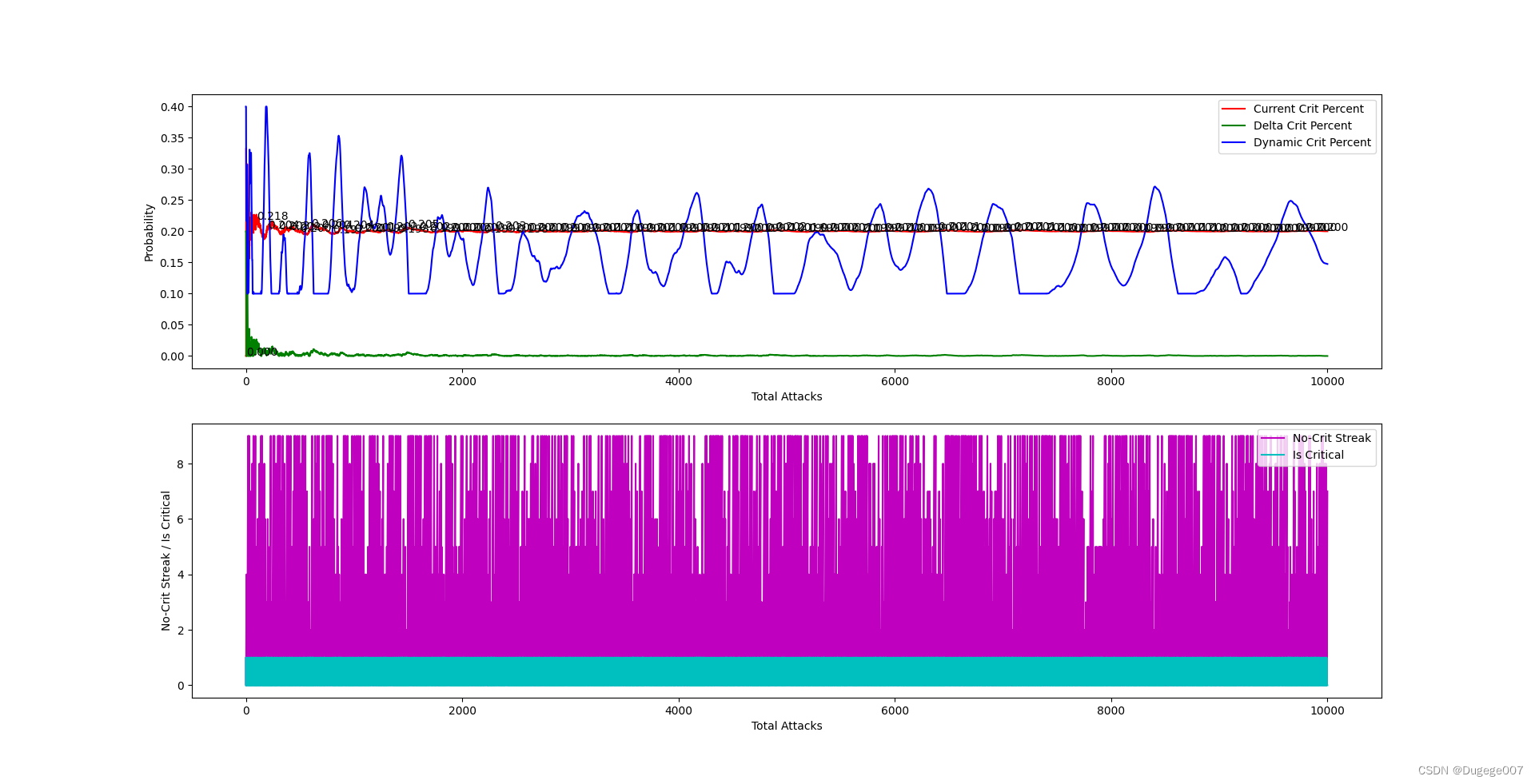
给定参数的运行结果如下图所示(这里的“要求N次攻击,至少有一次暴击”中的N,根据算法取了14)
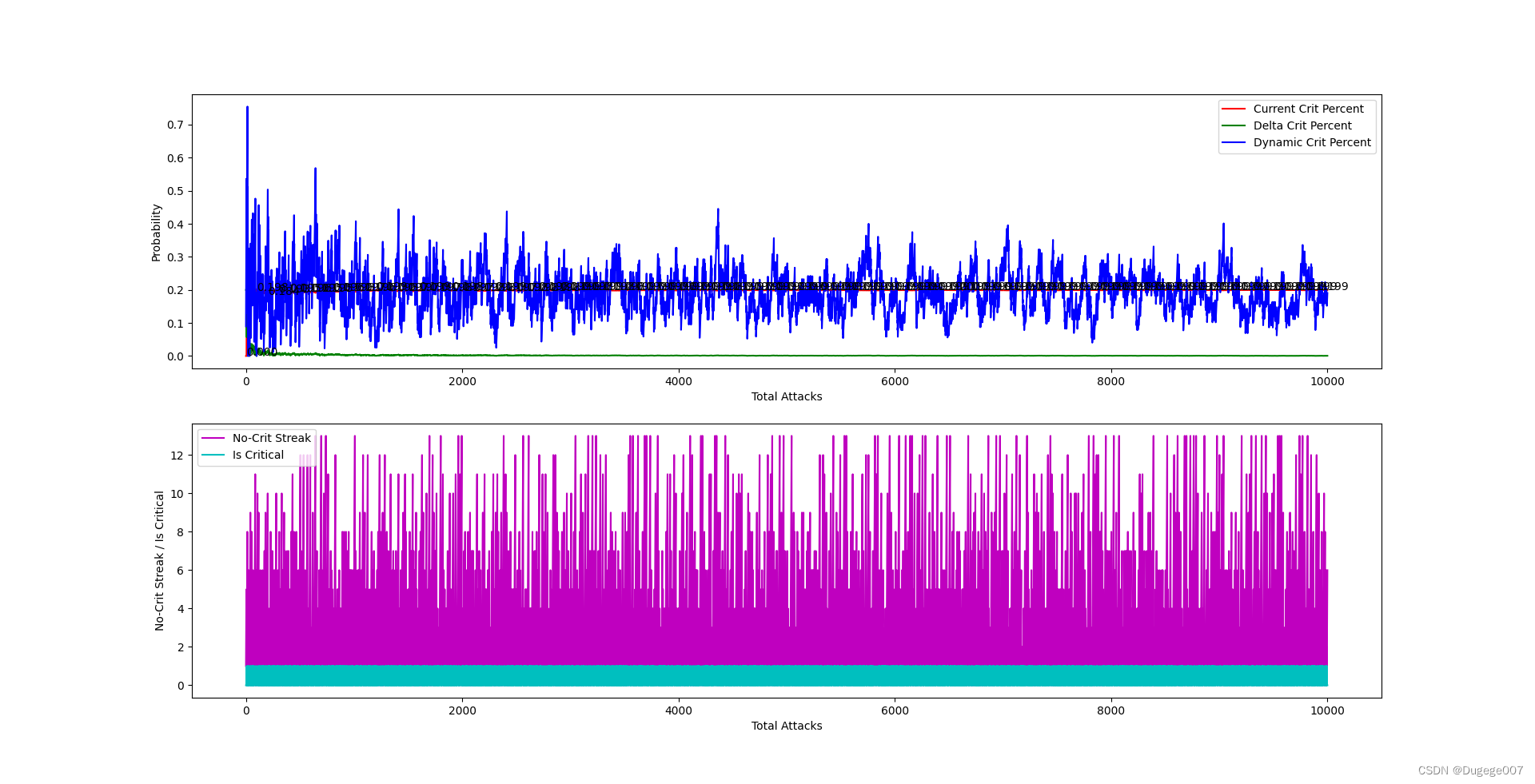
0 ~ 2000 次 如下
8000 ~ 10000 次 如下
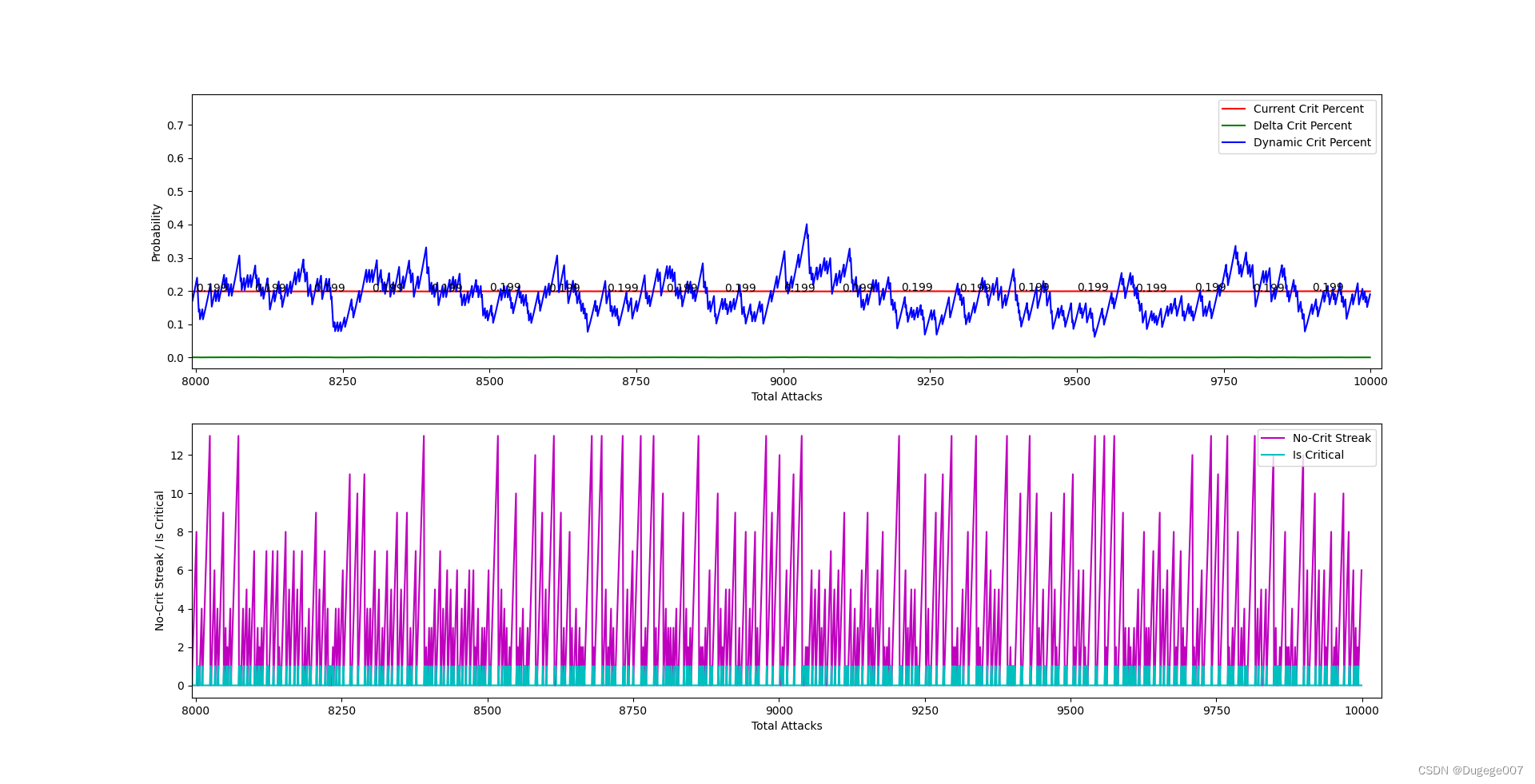
可以看出,总体暴击率会在大概300次内稳定下来,并且逐渐逼近 0.2;
在攻击次数足够多时,“动态暴击率”的浮动也会趋于稳定。
这是一种通过调整每次攻击的暴击率,来达到动态平衡效果的算法;
也可以说,这是一种动态调整每次概率,以达到目标数学期望的算法。
核心思路
以“暴击率”为例,以下是这种“动态平衡概率”算法的核心思路:
基本参数:
初始概率(目标概率)
:
P
动态概率
:
d
y
n
a
m
i
c
P
当前概率
:
c
u
r
r
e
n
t
P
概率差值
:
d
e
l
t
a
P
攻击次数
:
a
t
t
a
c
k
N
暴击次数
:
c
r
i
t
N
连续未暴击次数
:
n
o
C
r
i
t
S
t
r
e
a
k
\begin{align*} \text{初始概率(目标概率)} & :P \\ \text{动态概率} & :dynamicP \\ \text{当前概率} & :currentP \\ \text{概率差值} & :deltaP \\ \text{攻击次数} & :attackN \\ \text{暴击次数} & :critN \\ \text{连续未暴击次数} & :noCritStreak \\ \end{align*}
初始概率(目标概率)动态概率当前概率概率差值攻击次数暴击次数连续未暴击次数:P:dynamicP:currentP:deltaP:attackN:critN:noCritStreak
核心运算逻辑:
c
u
r
r
e
n
t
P
=
c
r
i
t
N
a
t
t
a
c
k
N
d
e
l
t
a
P
=
∣
P
−
c
u
r
r
e
n
t
P
∣
d
y
n
a
m
i
c
P
=
(
a
t
t
a
c
k
N
⋅
(
P
−
c
u
r
r
e
n
t
P
)
+
c
u
r
r
e
n
t
P
)
⋅
d
e
l
t
a
P
\begin{align*} currentP &= \frac{critN}{attackN} \\ deltaP &= |P - currentP| \\ dynamicP &= \left( attackN · (P - currentP) + currentP \right) · \sqrt{deltaP} \\ \end{align*}
currentPdeltaPdynamicP=attackNcritN=∣P−currentP∣=(attackN⋅(P−currentP)+currentP)⋅deltaP
暴击判断逻辑:
找到一个最佳的N,
用于判断连续 N - 1 次未暴击
:
Find_Optimal_N
(
p
)
:
(
1
−
p
)
N
≤
0.05
随机数生成和暴击判断
:
如果
n
o
C
r
i
t
S
t
r
e
a
k
<
N
−
1
,则生成一个随机数
p
e
r
c
e
n
t
;
﹂如果
p
e
r
c
e
n
t
≤
d
y
n
a
m
i
c
P
,则判定为暴击,相关参数 + 1
﹂否则 未暴击,相关参数 + 1
否则 必然暴击,相关参数 + 1
\begin{align*} \\ \text{找到一个最佳的N,} \\ \text{用于判断连续 N - 1 次未暴击} & : \\ \text{Find\_Optimal\_N}(p) & : (1 - p) ^ N \leq 0.05 \\ \\ \text{随机数生成和暴击判断} & : \\ & \text{如果 \(noCritStreak\) \( < N - 1 \),则生成一个随机数 \(percent\);} \\ & \text{ ﹂如果 \(percent\) \( \leq \) \(dynamicP\),则判定为暴击,相关参数 + 1} \\ & \text{ ﹂否则 未暴击,相关参数 + 1} \\ & \text{否则 必然暴击,相关参数 + 1} \\ \end{align*}
找到一个最佳的N,用于判断连续 N - 1 次未暴击Find_Optimal_N(p)随机数生成和暴击判断::(1−p)N≤0.05:如果 noCritStreak <N−1,则生成一个随机数 percent; ﹂如果 percent ≤ dynamicP,则判定为暴击,相关参数 + 1 ﹂否则 未暴击,相关参数 + 1否则 必然暴击,相关参数 + 1
本文到这里其实就结束了,这套算法虽然简单,但是笔者发现它的过程还是挺有意思的。
感兴趣的朋友可以继续往下看,文末还有一些优化思路…
发现
还是前文中的需求:
A. 暴击率总体为20%
B. 要求每十次攻击,至少有一次暴击
C. 要求暴击的总体分布较为均匀
假如每次暴击的概率都是0.2,并且每十次攻击至少一次暴击,这样相当于增加了总体最终的暴击数,也就是变相增加了暴击率,确实需要通过某种方式将最终结果调整到0.2.
目前笔者想到的实现方式大致分为两种:
一种是“动态概率”,我们可以随着实际已出现的概率,动态地调整下一次的概率,并保证在最终结果上符合我们的目标概率。
另一种是提前将“随机种子”做好。在制作“种子”时使用连续分段的、适当长度的数组,每段数组中目标出现的概率基本相同,且总体概率符合我们的目标概率。再人为打乱每段数组,最后将他们拼接起来。但是这种方式还有个问题,就是打乱数组之后可能会出现两个数组中的一个暴击在头一个在尾,两次暴击又会间隔较远的情况,无法完全保证 B 条件成立。
本文先尝试第一种方式————“动态概率”
以前面的需求为例,假如每次暴击的概率都是0.2,并且每十次攻击至少一次暴击,先这样在Unity中看一下最终的暴击率会高出多少
using UnityEngine;
public class CriticalHit : MonoBehaviour
{
// 初始暴击率
public float InitCritPercent = 0.2f;
// 当前暴击概率
private float currentCritPercent;
// 当前总攻击次数
private int attackTotalCount = 0;
// 当前总暴击过的次数
private int critTotalCount = 0;
// 连续未出现暴击的次数
private int noCritStreakCount = 0;
private void Start()
{
currentCritPercent = InitCritPercent;
}
private void Update()
{
// 监听鼠标左键输入
if (Input.GetMouseButtonDown(0))
{
// 测试一次
PerformAttack();
Debug.Log("当前暴击率:" + currentCritPercent);
}
if (Input.GetKeyDown(KeyCode.Space))
{
// 测试一万次
for (int i = 0; i < 10000; i++) PerformAttack();
}
}
private void PerformAttack()
{
attackTotalCount++;
bool isCritical = false;
if (attackTotalCount > 0)
{
// 计算当前暴击概率 = 总暴击数 / 总攻击数
currentCritPercent = (float)critTotalCount / attackTotalCount;
}
// 检查是否需要强制暴击
if (noCritStreakCount < 9)
{
float percent = Random.Range(0f, 1f);
if (percent < InitCritPercent)
{
isCritical = true;
noCritStreakCount = 0; // 重置计数器
}
else
{
noCritStreakCount++;
}
}
else
{
isCritical = true;
noCritStreakCount = 0; // 重置计数器
}
if (isCritical) critTotalCount++;
// 执行攻击,如果 isCritical 为 true,则为暴击
if (isCritical)
Debug.Log("Critical Hit!");
else
Debug.Log("Normal Hit.");
}
}
将这个脚本挂到场景中的空物体上,运行游戏,然后按空格键先测试一万次,再点击鼠标左键显示当前的暴击率
用上述方式测试几次,会发现最终的暴击率大概在 22.5% 左右,打印结果如下图所示
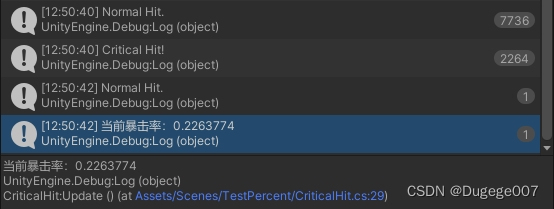
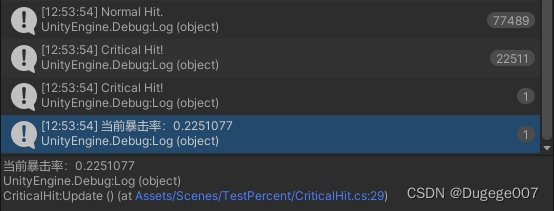
那么这多出来的 2.5% 为什么会是 2.5% 呢,它具体是怎么来的呢,如何避免它产生呢?
带着这样的疑惑,笔者开始尝试进行分析…
排除误差的可能
首先我们要排除这 2.5% 是误差的可能。
假设暴击率为 0.2,不考虑其他的设定和限制,每次测试十万次、共测试三次。
那么正常情况下的输出结果如下图所示
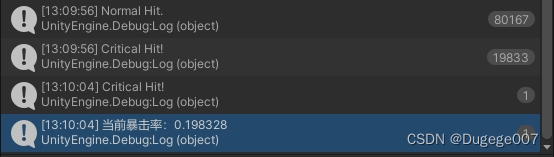
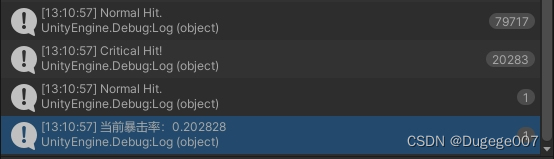
误差在 0.2% 左右,这与 2.5% 差别还是很大的,所以基本排除这是误差导致的情况。
探索
为了进一步优化算法,笔者决定结合已有的数据和个人直觉进行改进。
笔者用Python重新编写了一版代码,这样我们不仅可以方便地输出图表进行可视化分析,还能在这个基础上进行后续的代码修改和优化。
import matplotlib.pyplot as plt
import random
# 初始化变量
InitCritPercent = 0.2 # 初始暴击率
attackTotalCount = 0 # 总攻击次数
critTotalCount = 0 # 总暴击次数
noCritStreakCount = 0 # 连续未暴击次数
# 给 plot 准备的列表
currentCritPercentList = []
noCritStreakCountList = []
isCriticalList = []
# 测试 10000 次
for i in range(10000):
attackTotalCount += 1
isCritical = False
# 检查是否连续 9 次未暴击
if noCritStreakCount < 9:
percent = random.random()
if percent <= InitCritPercent:
isCritical = True
noCritStreakCount = 0
else:
noCritStreakCount += 1
else:
isCritical = True
noCritStreakCount = 0
if isCritical:
critTotalCount += 1
# 计算当前暴击概率
currentCritPercent = critTotalCount / attackTotalCount
# 添加数据到列表中
currentCritPercentList.append(currentCritPercent)
noCritStreakCountList.append(noCritStreakCount)
isCriticalList.append(int(isCritical))
# 创建多表格
fig, axs = plt.subplots(2)
# 画出暴击概率数据表格
axs[0].plot(currentCritPercentList, label='Current Crit Percent', color='r')
axs[0].set_xlabel('Total Attacks')
axs[0].set_ylabel('Probability')
axs[0].legend()
# 每 100 条数据标注一下
for i in range(0, len(currentCritPercentList), 100):
axs[0].annotate(f"{currentCritPercentList[i]:.5f}", (i, currentCritPercentList[i]))
# 画出连续未暴击次数的表格
axs[1].plot(noCritStreakCountList, label='No-Crit Streak', color='m')
axs[1].plot(isCriticalList, label='Is Critical', color='c')
axs[1].set_xlabel('Total Attacks')
axs[1].set_ylabel('No-Crit Streak / Is Critical')
axs[1].legend()
plt.show()
从输出的图表中不难看出,整体的暴击率确实变高了,如下图所示
前 2000 次 如下
8000 ~ 10000 次 如下
如要将最终的暴击概率调整回 0.2,那就应该降低“当前暴击概率”,将 B 条件所增加的那部分修正回来。
“递增修正”
将前文的python代码添加几个变量,用来检测当前暴击概率的变化,当前暴击概率高于初始暴击率的时候,就降低动态暴击率,直到将当前暴击率拉回到正常水平;反之亦然。
import matplotlib.pyplot as plt
import random
# 初始化变量
InitCritPercent = 0.2 # 初始暴击率
currentCritPercent = 0 # 当前暴击概率
deltaCritPercent = 0 # 当前暴击率与初始暴击率的差值(用来表示变化)
dynamicCritPercent = 0.2 # 动态暴击率
attackTotalCount = 0 # 总攻击次数
critTotalCount = 0 # 总暴击次数
noCritStreakCount = 0 # 连续未暴击次数
# 给 plot 准备的列表
currentCritPercentList = []
deltaCritPercentList = []
dynamicCritPercentList = []
noCritStreakCountList = []
isCriticalList = []
# 测试 10000 次
for i in range(10000):
attackTotalCount += 1
isCritical = False
# 检查是否连续 9 次未暴击
if attackTotalCount > 0:
# 计算当前暴击概率
currentCritPercent = critTotalCount / attackTotalCount
# 计算当前暴击概率与初始暴击率的差值
deltaCritPercent = abs(InitCritPercent - currentCritPercent)
# 计算动态暴击率
if(currentCritPercent > InitCritPercent):
dynamicCritPercent -= deltaCritPercent
if(currentCritPercent < InitCritPercent):
dynamicCritPercent += deltaCritPercent
# 检查是否连续 9 次未暴击
if noCritStreakCount < 9:
percent = random.random()
if percent <= dynamicCritPercent:
isCritical = True
noCritStreakCount = 0
else:
noCritStreakCount += 1
else:
isCritical = True
noCritStreakCount = 0
if isCritical:
critTotalCount += 1
# 将数据添加到列表中
currentCritPercentList.append(currentCritPercent)
deltaCritPercentList.append(deltaCritPercent)
dynamicCritPercentList.append(dynamicCritPercent)
noCritStreakCountList.append(noCritStreakCount)
isCriticalList.append(int(isCritical))
# 创建多表格
fig, axs = plt.subplots(2)
# 每 100 条数据标注一下
for i in range(0, len(currentCritPercentList), 100):
axs[0].annotate(f"{currentCritPercentList[i]:.3f}", (i, currentCritPercentList[i]))
# 画出暴击概率数据表格
axs[0].plot(currentCritPercentList, label='Current Crit Percent', color='r')
axs[0].plot(deltaCritPercentList, label='Delta Crit Percent', color='g')
axs[0].plot(dynamicCritPercentList, label='Dynamic Crit Percent', color='b')
axs[0].set_xlabel('Total Attacks')
axs[0].set_ylabel('Probability')
axs[0].legend()
# 画出连续未暴击次数的表格
axs[1].plot(noCritStreakCountList, label='No-Crit Streak', color='m')
axs[1].plot(isCriticalList, label='Is Critical', color='c')
axs[1].set_xlabel('Total Attacks')
axs[1].set_ylabel('No-Crit Streak / Is Critical')
axs[1].legend()
plt.show()
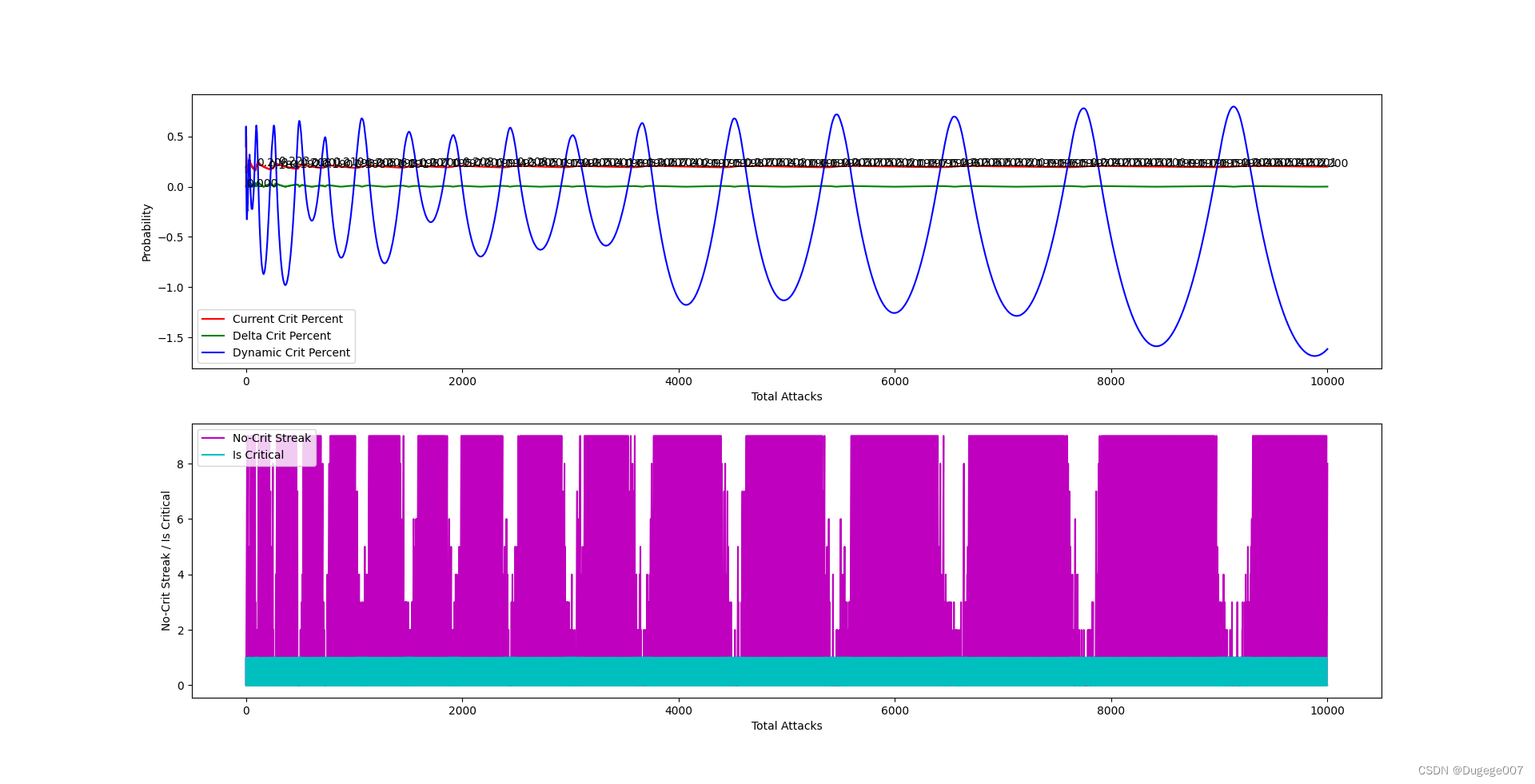
输出结果如下图所示
前 2000 次 如下
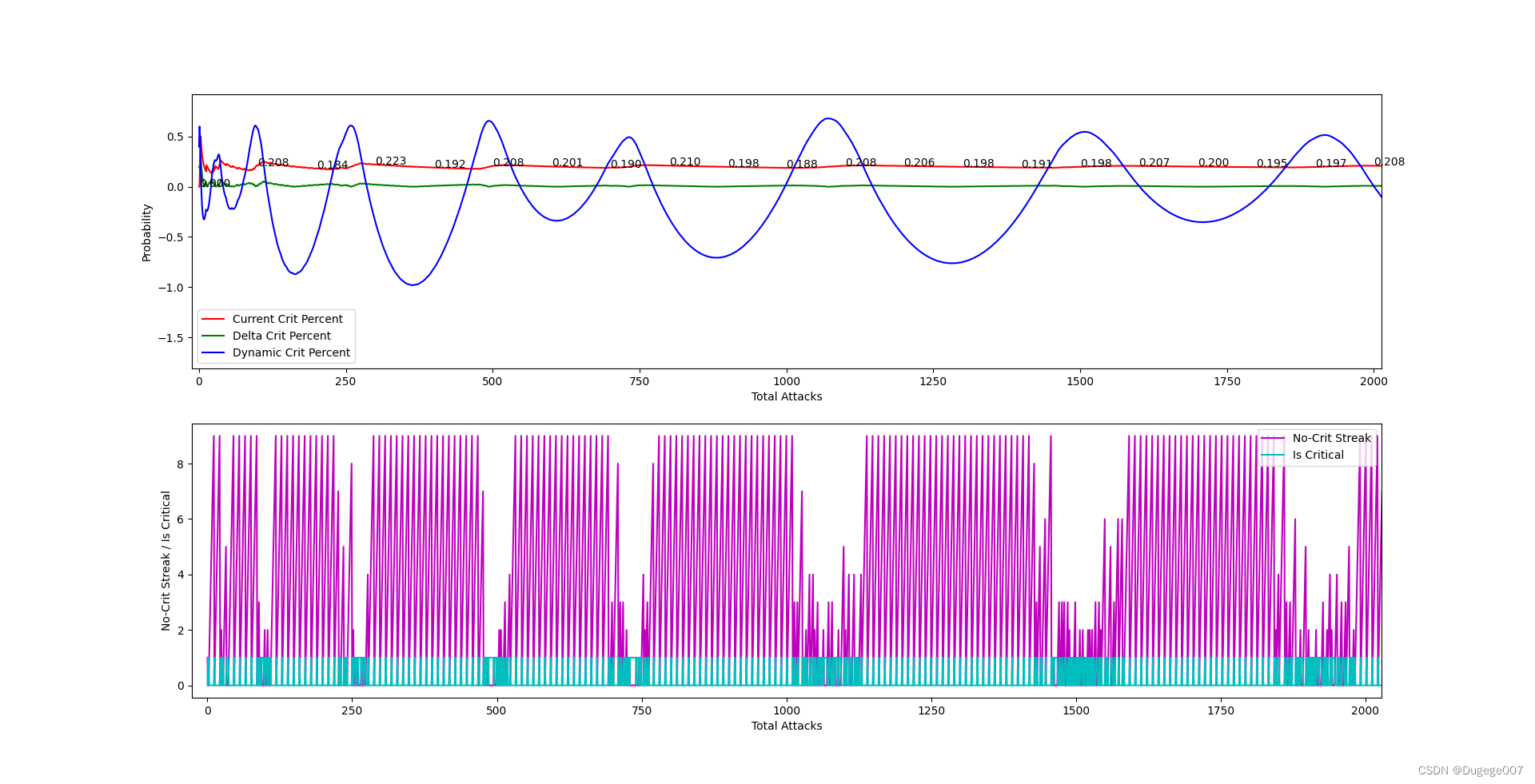
可以明显看出动态暴击率在大幅度地反复震荡,并且明显超出了 (0, 1) 的区间;
在震荡的高点时,会出现连续暴击的情况;在震荡的低点时,会出现连续地触发“保底”暴击;
这样虽然能将总体暴击概率稳定在 0.2 左右,但这显然不满足条件 C。
“递增修正”优化
显而易见,当动态暴击率超出 (0, 1) 区间时,就和 0、1 没有区别了
所以可以为它加个简单限幅,例如笔者将动态暴击率的幅度限制在(0.5倍初始暴击率,2倍初始暴击率)之间
# 同上文代码
# 测试 10000 次
for i in range(10000):
# 同上文代码
if attackTotalCount > 0:
# 同上文代码
# 计算动态暴击率
if(currentCritPercent > InitCritPercent):
dynamicCritPercent = min(max(dynamicCritPercent - deltaCritPercent, InitCritPercent * 0.5), InitCritPercent * 2)
if(currentCritPercent < InitCritPercent):
dynamicCritPercent = min(max(dynamicCritPercent + deltaCritPercent, InitCritPercent * 0.5), InitCritPercent * 2)
# 检查是否连续 9 次未暴击
if noCritStreakCount < 9:
# 同上文代码
# 同上文代码
# 同上文代码
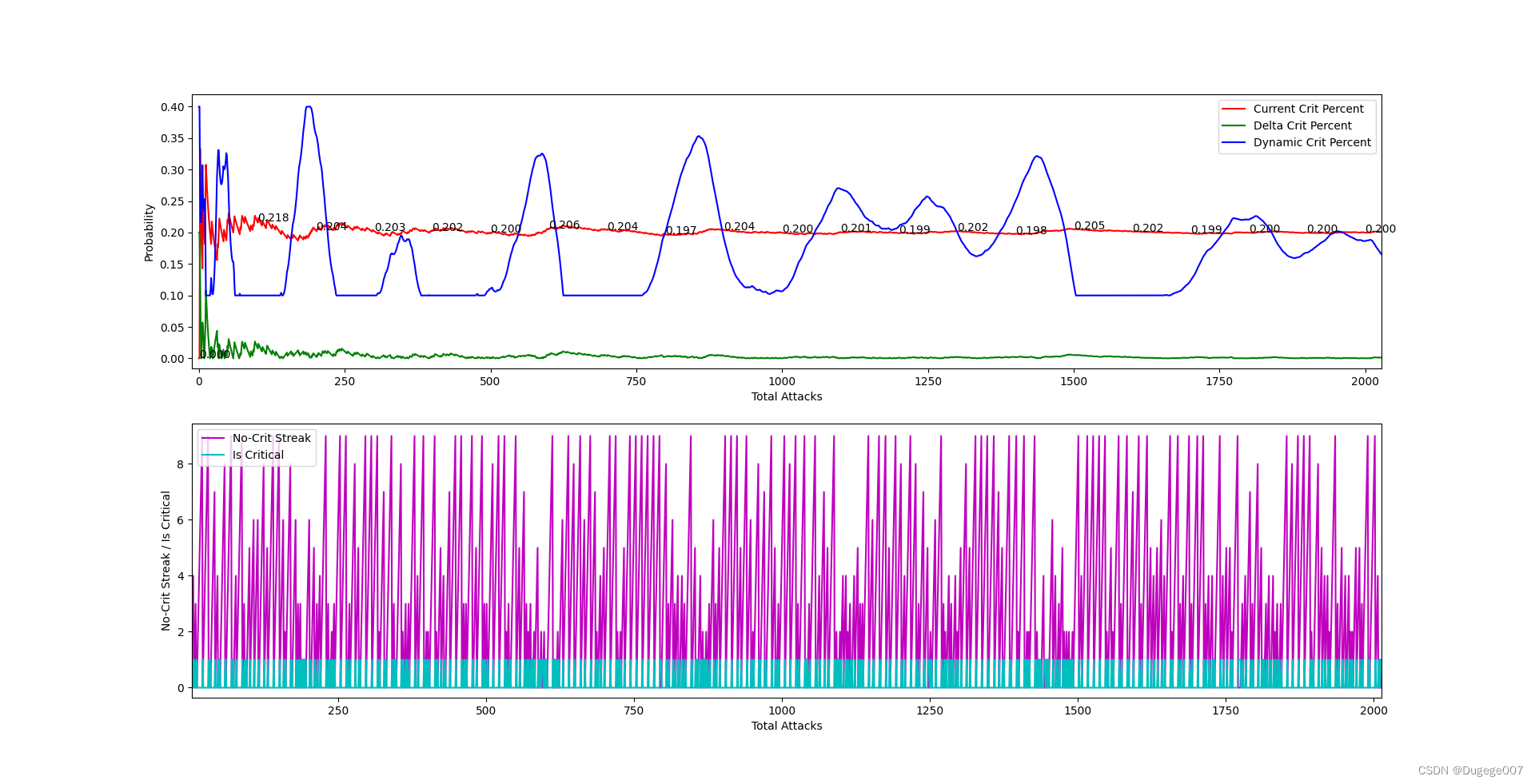
输出结果如下图所示
前 2000 次 如下
8000 ~ 10000 次 如下
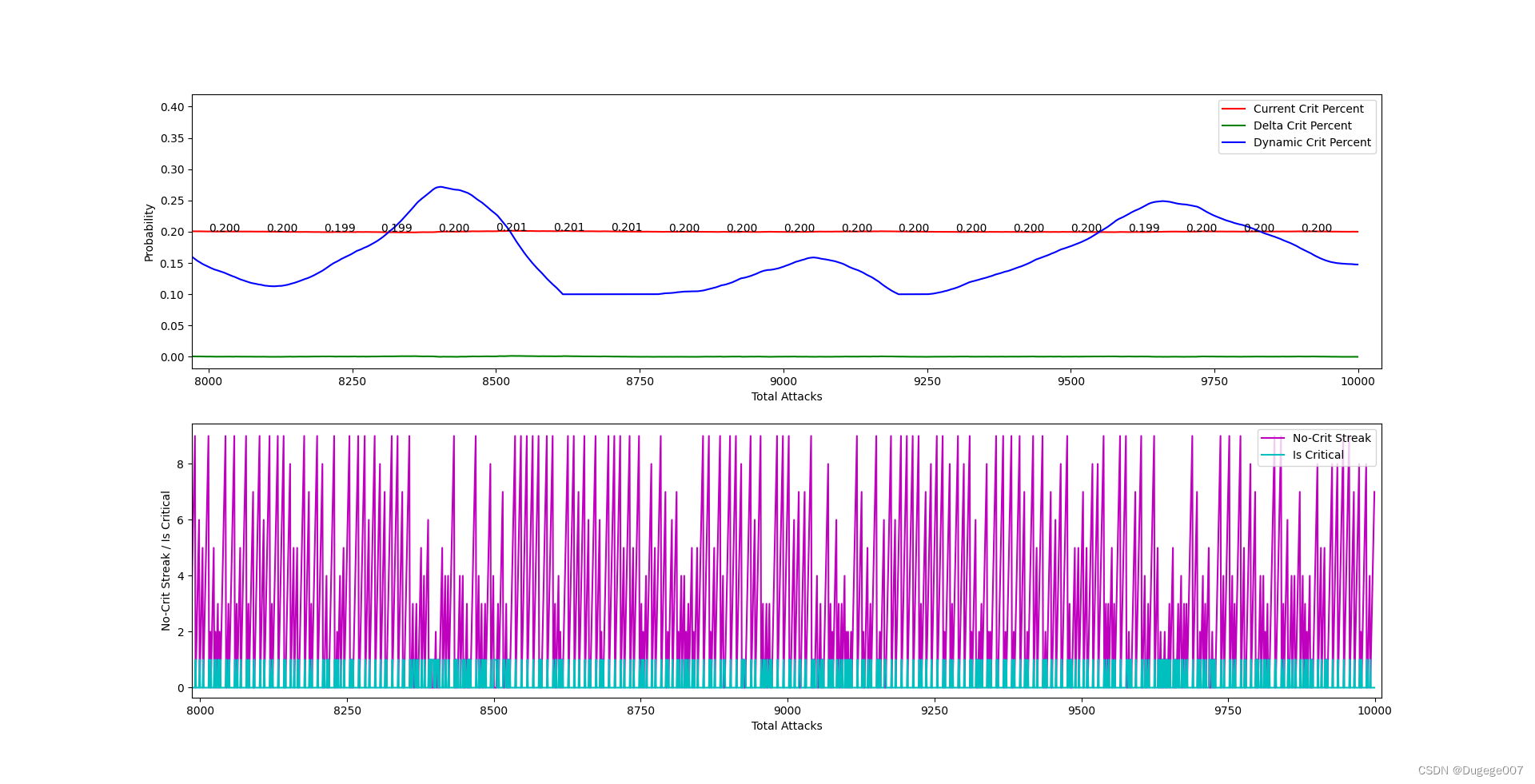
现在的算法已经基本可用了,但还需要多尝试才能找到合适的限幅范围。
当限幅范围过大时,概率的分布会变得不均匀;
限幅范围过小时,又会出现无法逼近目标概率(初始暴击率),比较麻烦。
“递增修正”测试
将上述优化过的算法应用到其他情景中,例如掷硬币,每5次投掷至少有一次正面
初始概率(目标概率) = 0.5
# 同上文代码
InitCritPercent = 0.5
dynamicCritPercent = 0.5
# 同上文代码
# 测试 10000 次
for i in range(10000):
# 同上文代码
# 检查是否连续 4 次未掷出正面
if noCritStreakCount < 4:
# 同上文代码
# 同上文代码
# 同上文代码
输出结果如下图所示
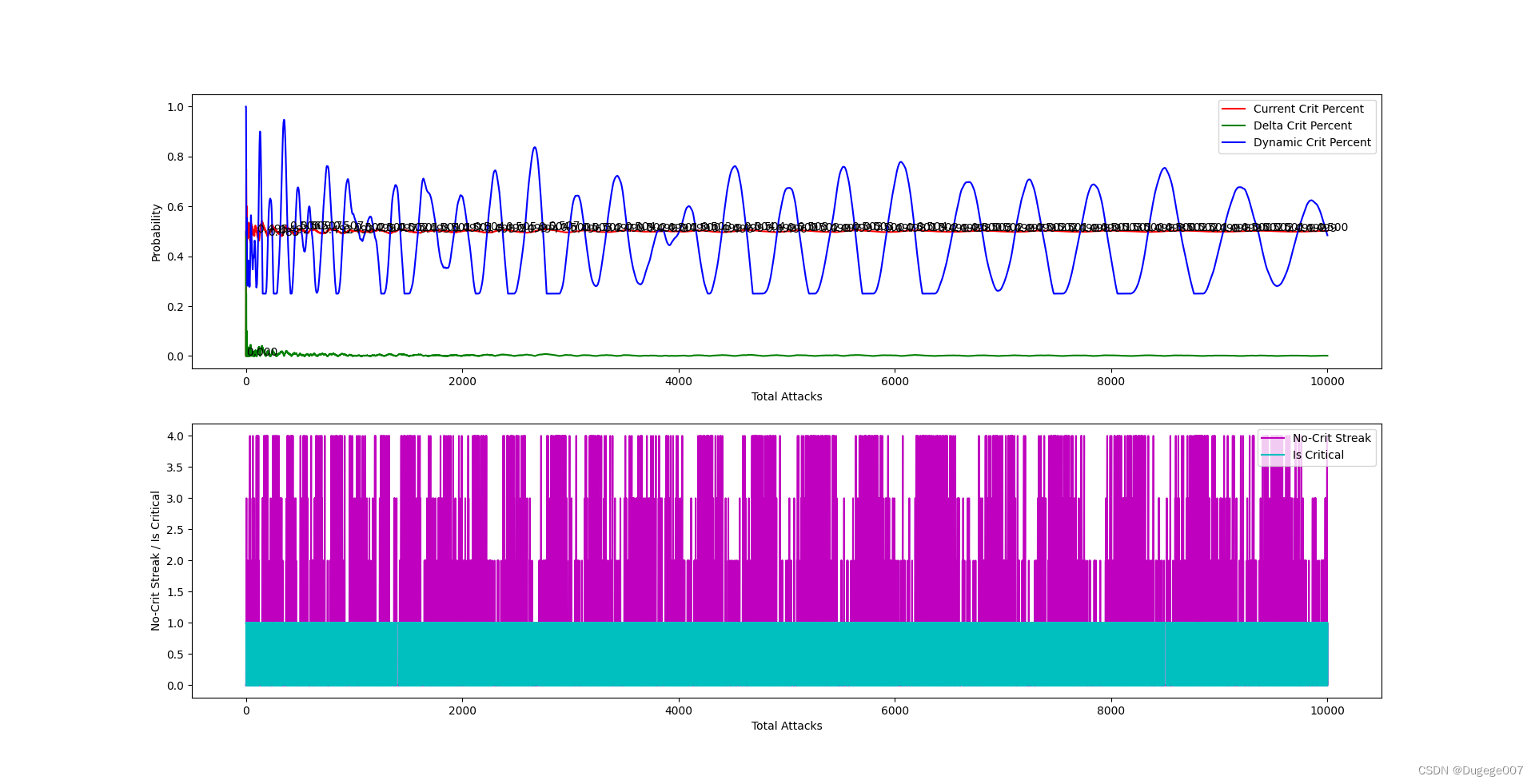
前 2000 次 如下
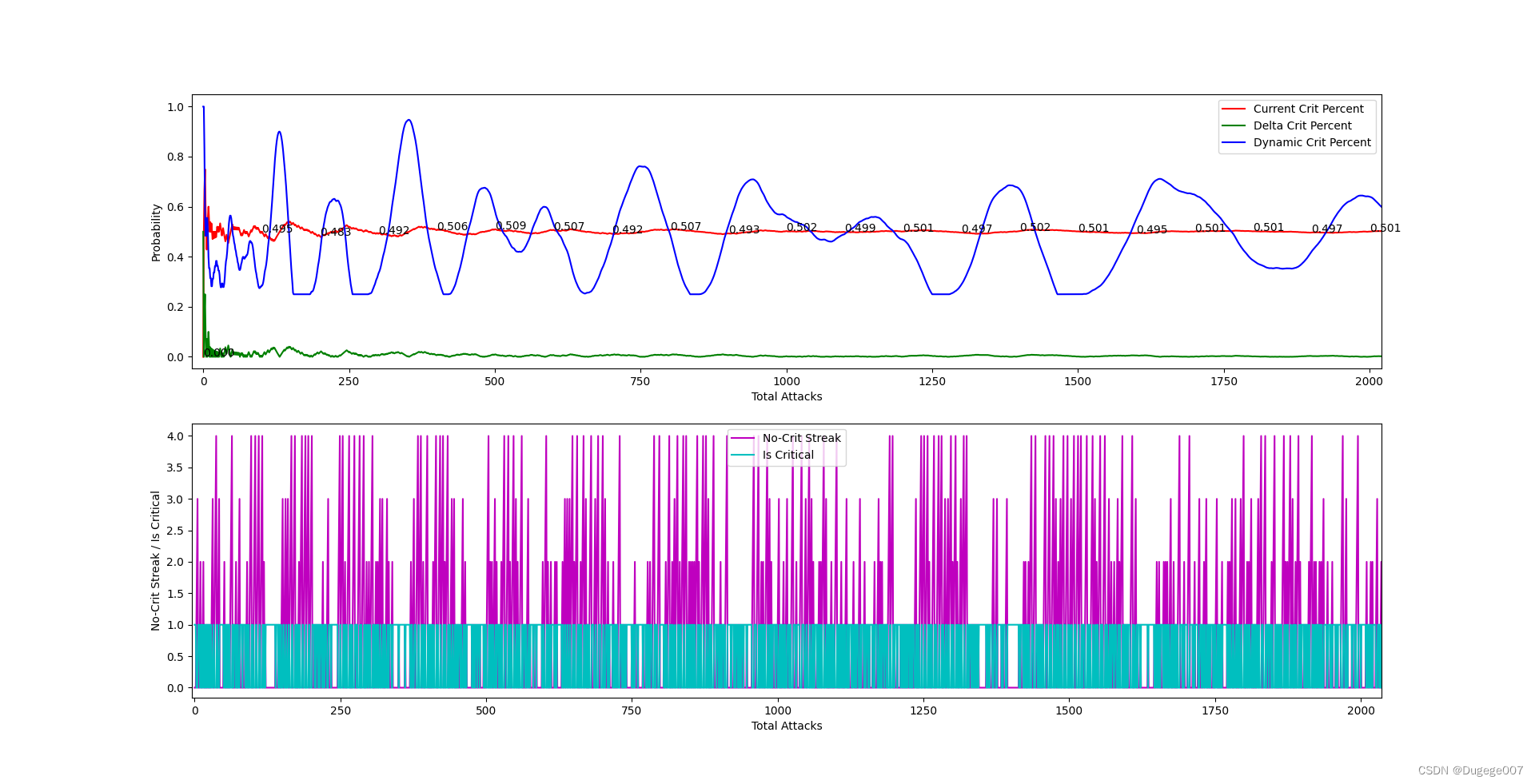
8000 ~ 10000 次 如下
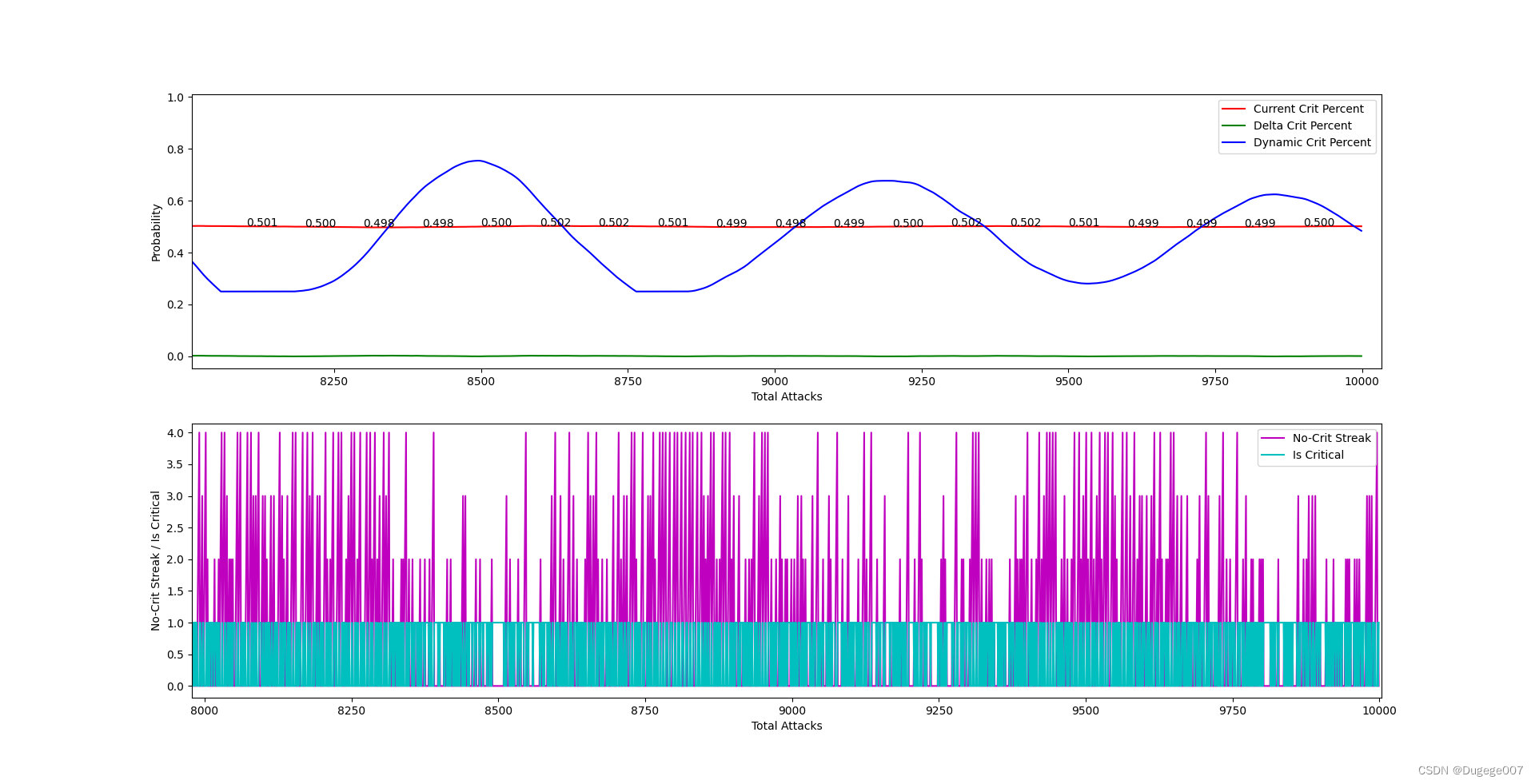
可以发现出现连续未正面的次数(连续未暴击次数),又在动态概率的波谷处出现“聚拢”现象,这很好理解:因为我们的限幅有些过大了。
总结下来,这种手动限定幅度的方式效率很低还容易出问题…
那么能不能让它根据自身目前状况,如目标概率、总攻击次数等参数,来动态调整 动态暴击率的增量呢?
“镜像修正”
基于以上思考,笔者希望每次攻击的“动态暴击率”是上次“当前暴击概率”关于“初始暴击率”的镜像,通过这种有针对性的“反向”操作,来将最终暴击率逼近目标值。
于是便有如下代码:
# 初始化变量
InitCritPercent = 0.2 # 初始暴击率
dynamicCritPercent = 0.2 # 动态暴击率
# 同上文代码
# 测试 10000 次
for i in range(10000):
# 同上文代码
if attackTotalCount > 0:
# 同上文代码
# 计算动态暴击率
dynamicCritPercent = attackTotalCount * InitCritPercent - (attackTotalCount - 1) * currentCritPercent
# 检查是否连续 9 次未暴击
if noCritStreakCount < 9:
# 同上文代码
# 同上文代码
# 同上文代码
输出结果如下图所示
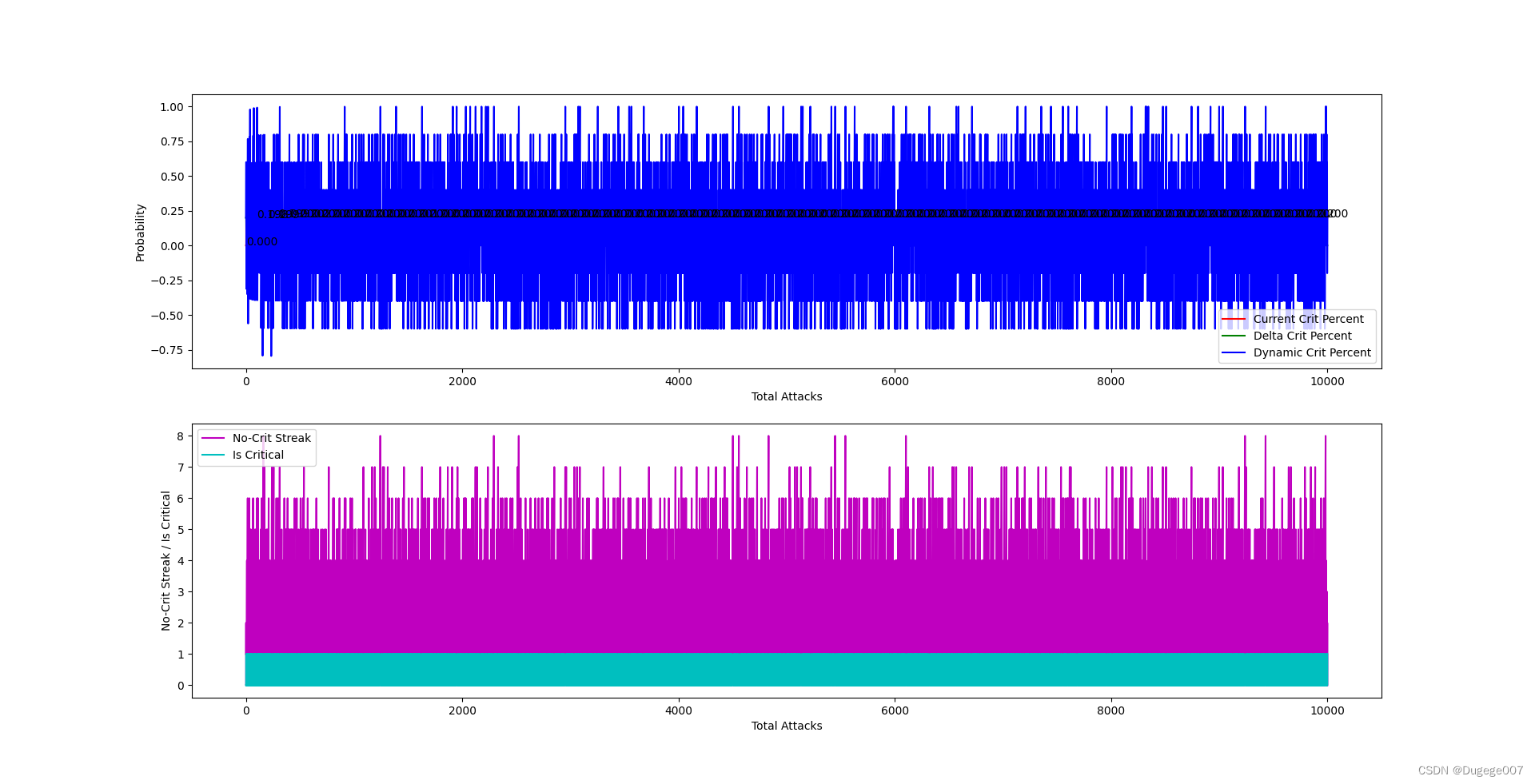
前 2000 次 如下
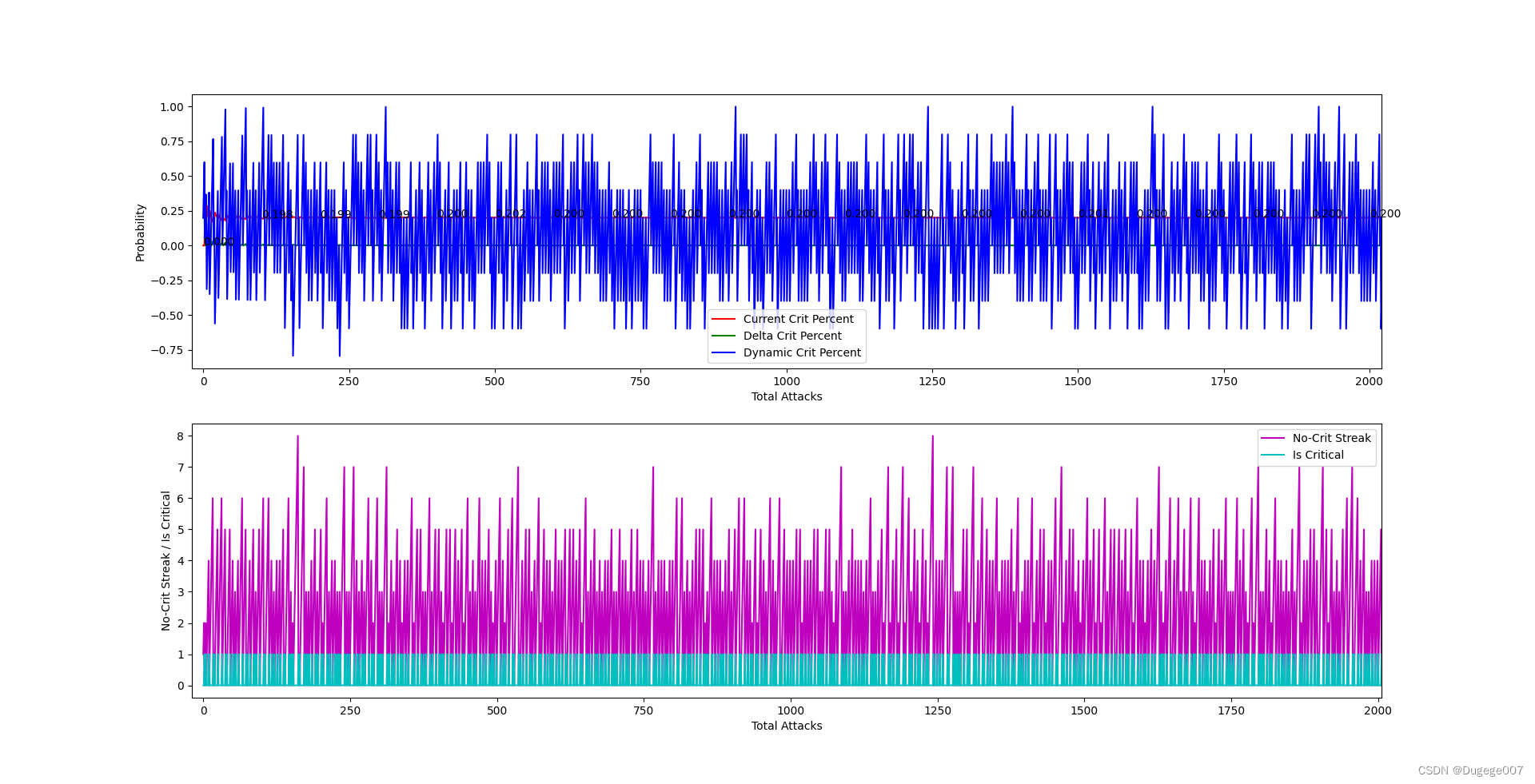
8000 ~ 10000 次 如下
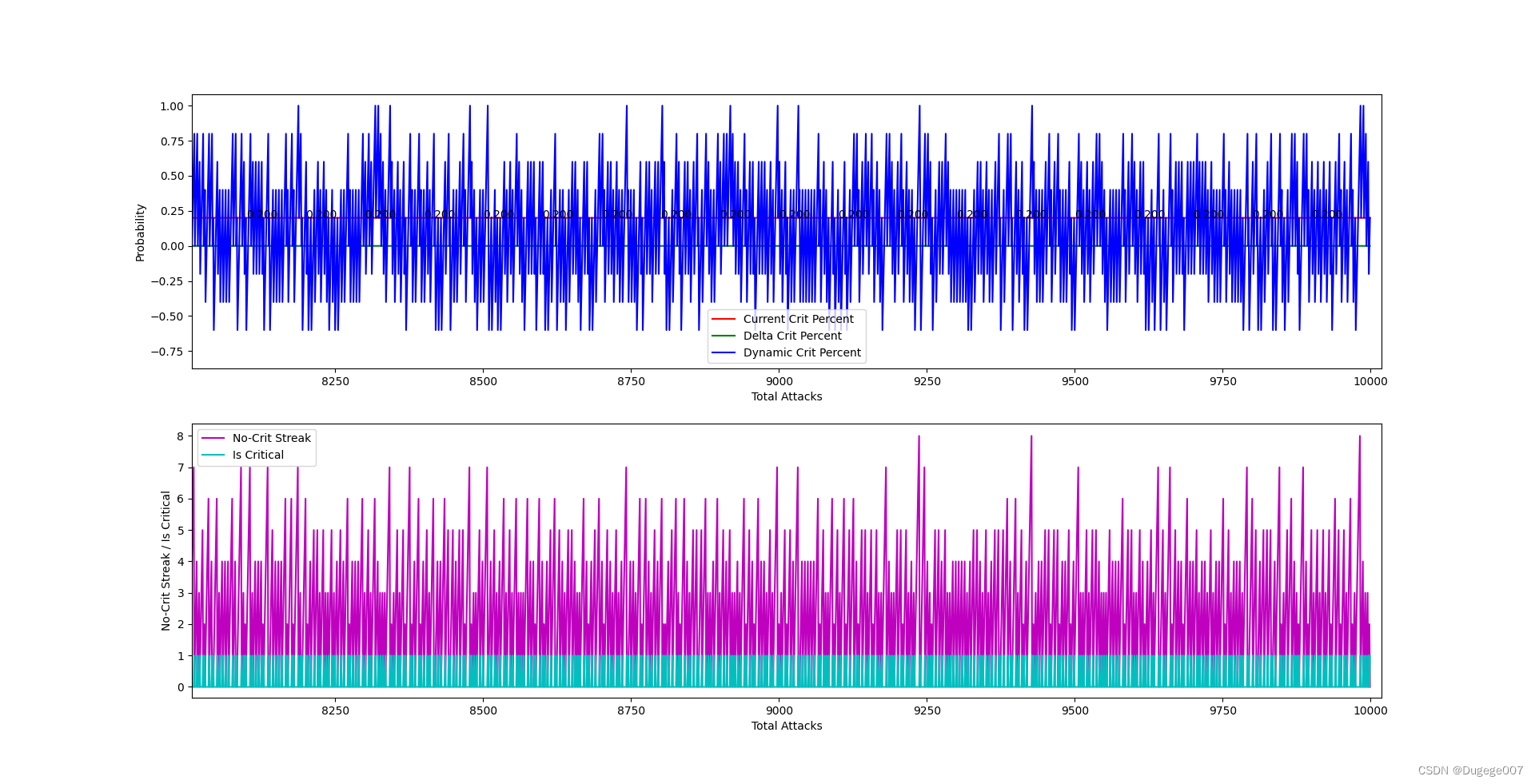
虽然能将最终的暴击概率稳定在 0.2,但结果过于平均了!
可以说这种“修正”的操作过于灵敏,导致暴击的分布非常均匀,甚至没有出现连续 9 次以上的未暴击。但这仍不是我们想要的,需要继续优化。
“镜像修正”优化
笔者发现,这种“过于均匀”的分布情况也是因为每次修正幅度过大导致的。
现在要调整这个幅度会比“递增修正”的方法容易很多,只需要让“计算动态暴击率”的结果乘以一个较小的系数即可。
这个系数需要与当前的状态有关,并且是一个越来越小的值。
而在攻击次数越来越多时,currentCritPercent 也会越来越逼近 InitCritPercent 的值,所以 deltaCritPercent 会随着攻击次数的增多越来越小;
(又因为 currentCritPercent 趋向于一个比 InitCritPercent 偏大的值,那么 deltaCritPercent 也会永不为 0)
这里我们就用 deltaCritPercent 来作为系数,目前来看刚好合适。
# 同上文代码
# 计算动态暴击率
dynamicCritPercent = (attackTotalCount * (InitCritPercent - currentCritPercent) + currentCritPercent) * deltaCritPercent
# 同上文代码
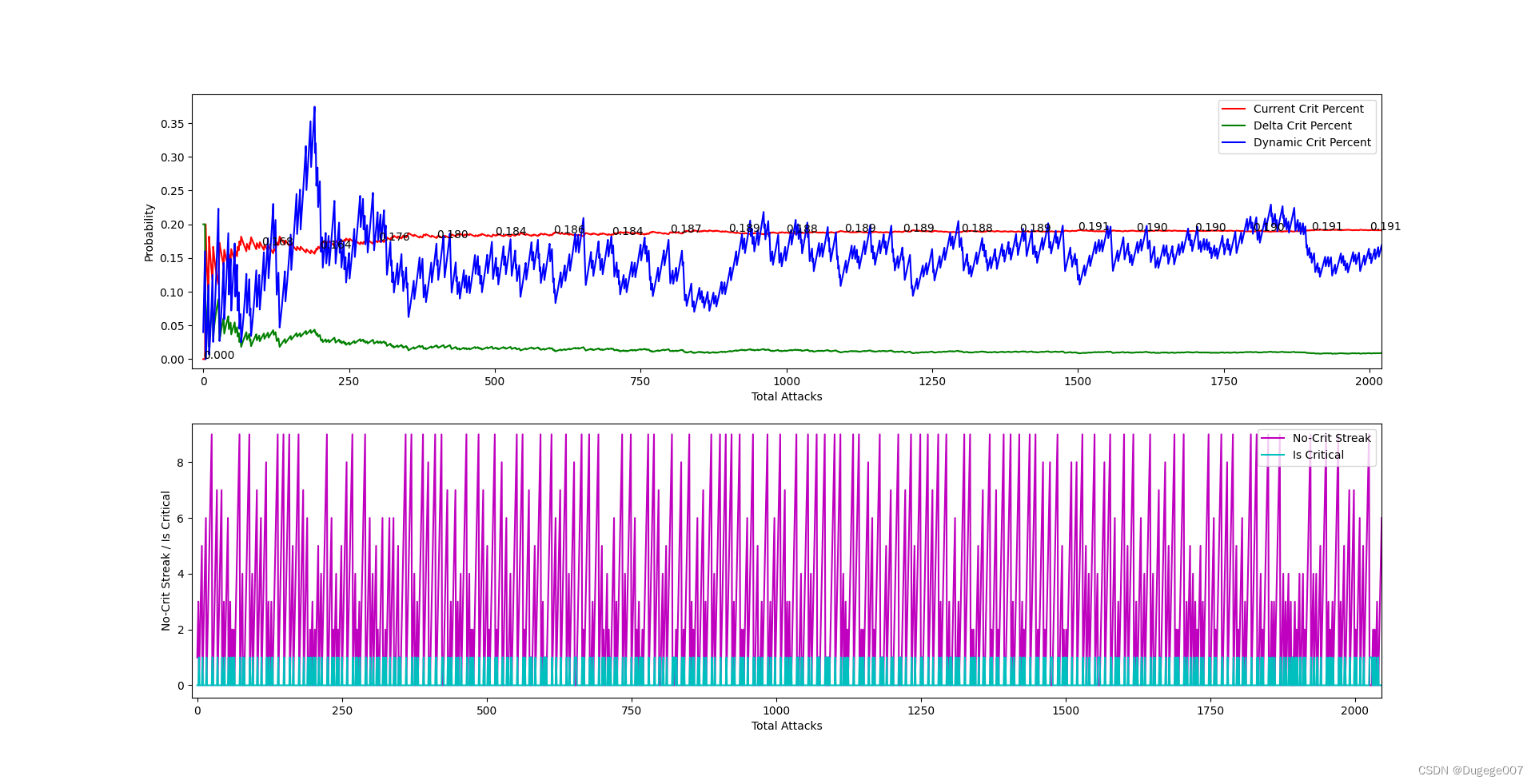
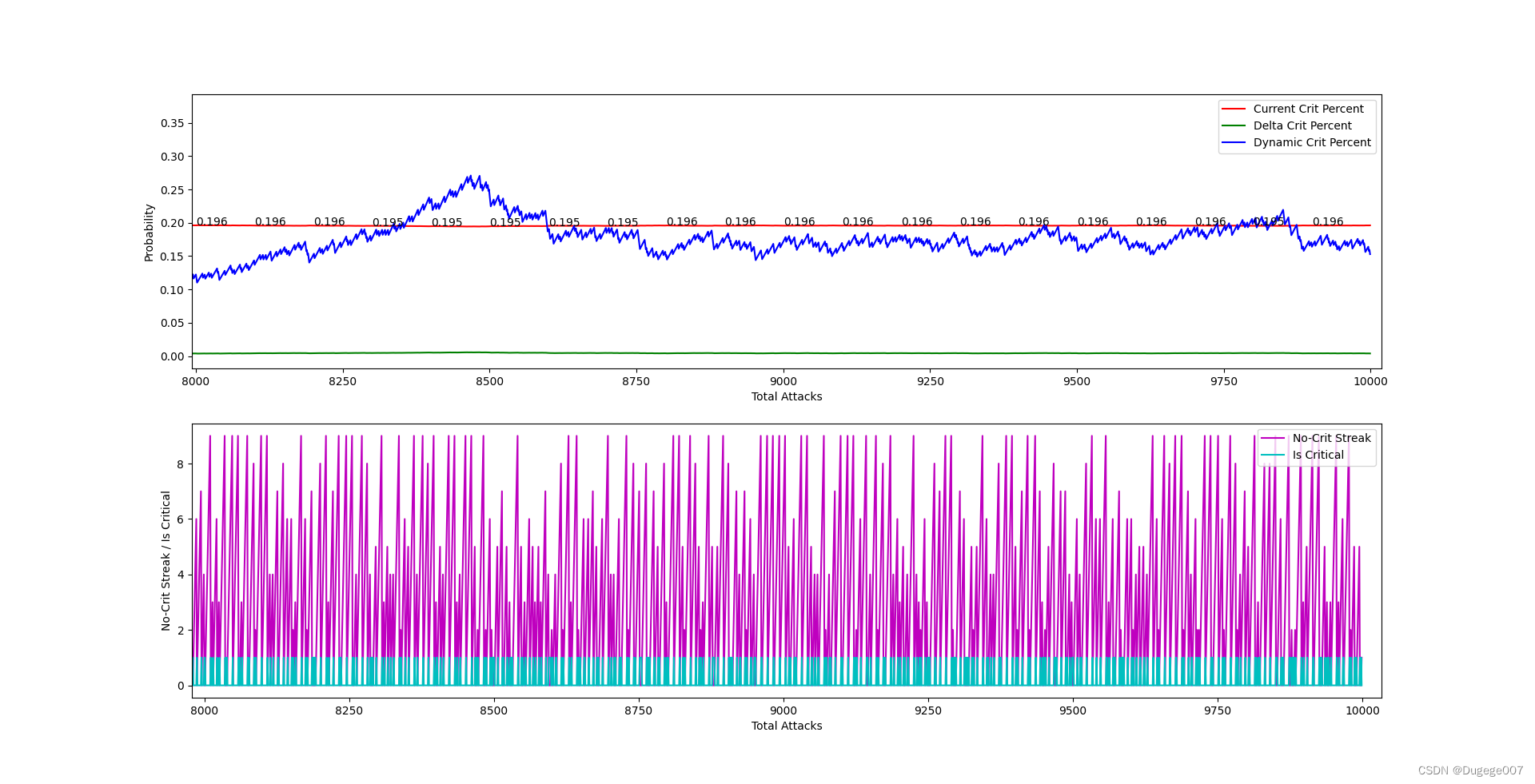
输出结果如下图所示
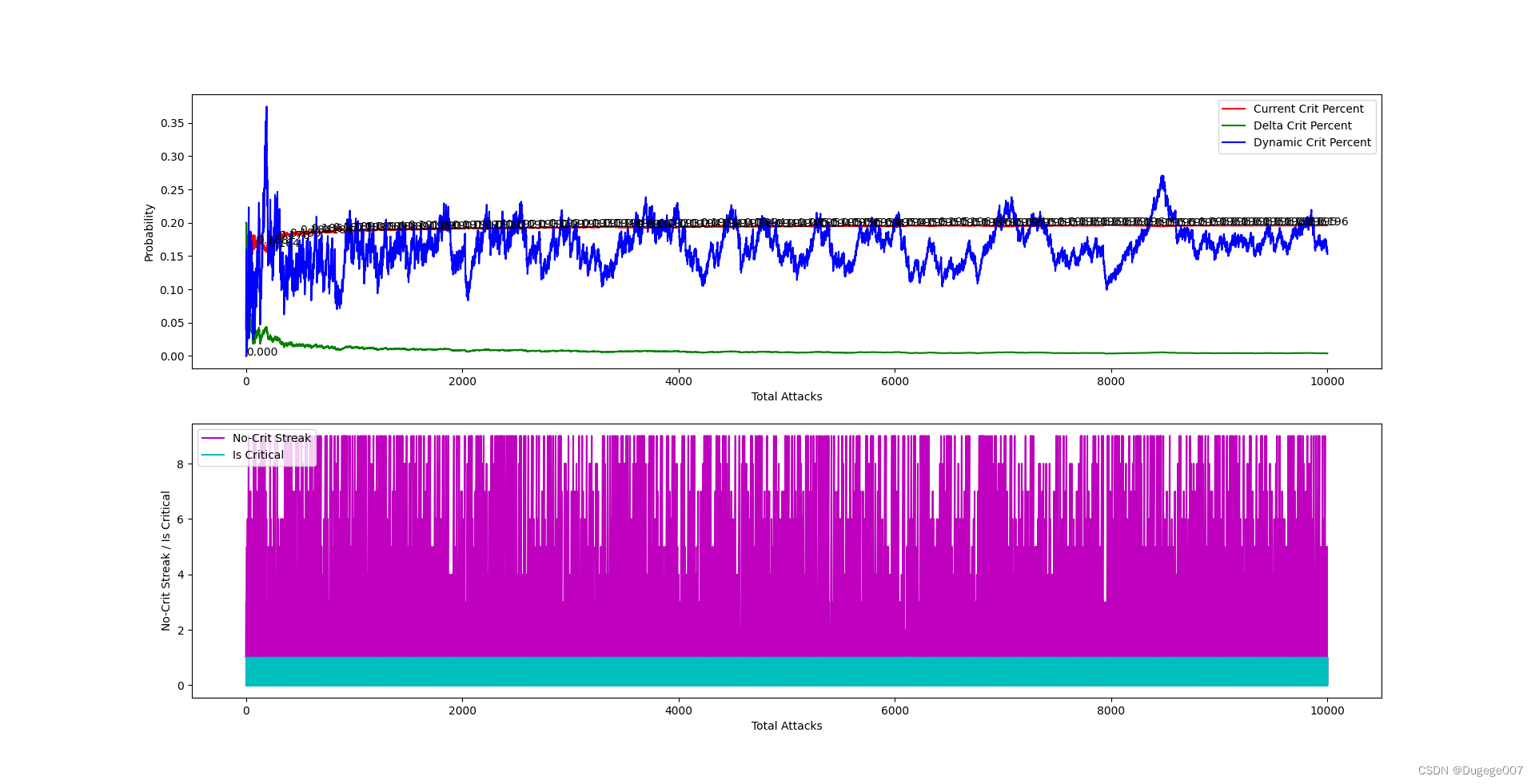
前 2000 次 如下
8000 ~ 10000 次 如下
由于对每次的 dynamicCritPercent 的幅度都做了差不多的限制,可以看到图二中,在前 1000 次左右攻击时,currentCritPercent 逼近目标值的速度很慢。
啧,还差一点…
继续优化!既然 deltaCritPercent 会随着攻击次数增多变得越来越小,那么我们不妨直接将它放大。
# 同上文代码
# 计算动态暴击率
dynamicCritPercent = (attackTotalCount * (InitCritPercent - currentCritPercent) + currentCritPercent) * pow(deltaCritPercent, 0.5)
# 同上文代码
输出结果如下图所示
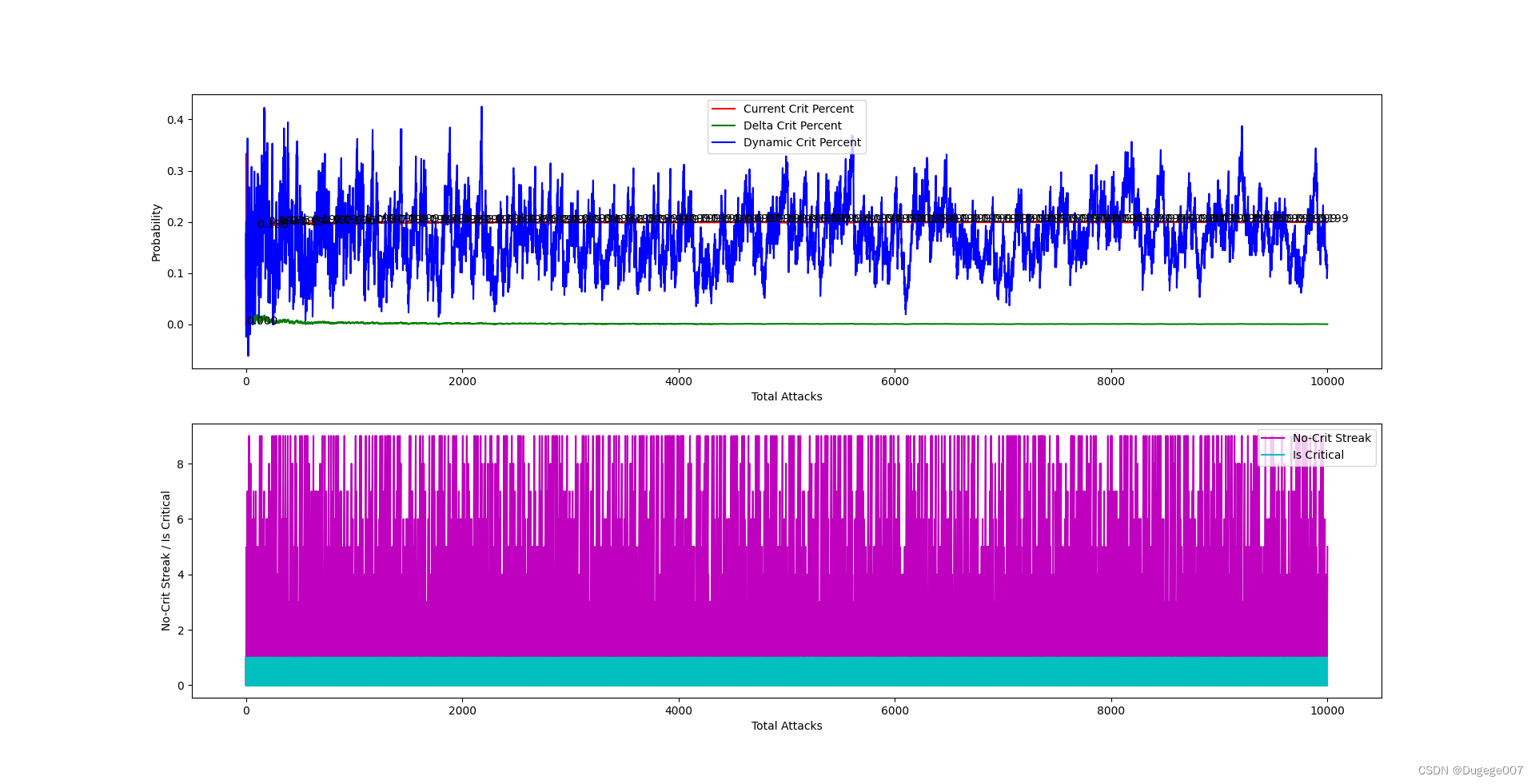
前 2000 次 如下
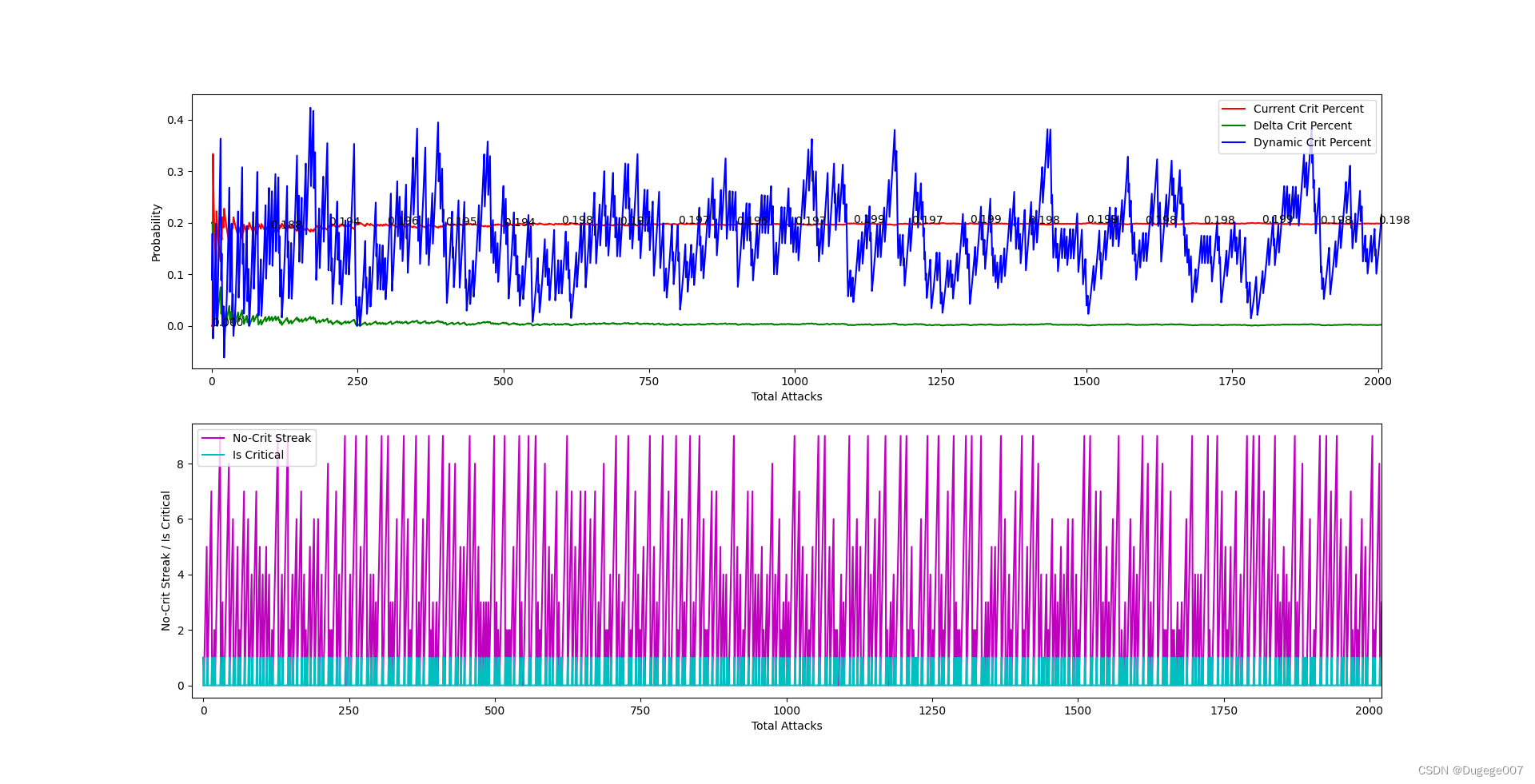
8000 ~ 10000 次 如下
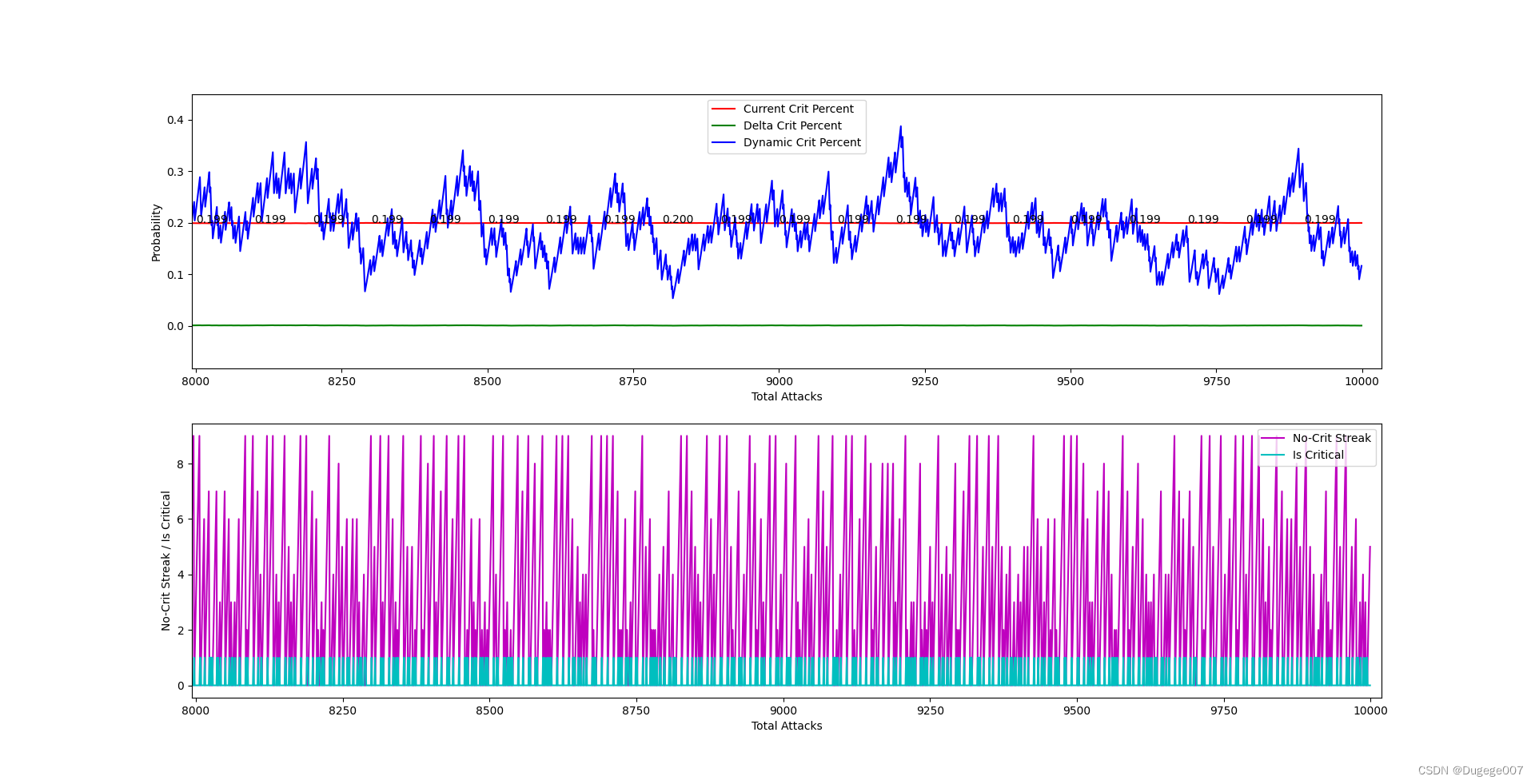
以上结果已经基本符合预期。
“镜像修正”测试
掷硬币
下面还是用硬币的例子:掷硬币,每5次投掷至少有一次正面
初始概率(目标概率) = 0.5
# 同上文代码
InitCritPercent = 0.5
dynamicCritPercent = 0.5
# 同上文代码
# 测试 10000 次
for i in range(10000):
# 同上文代码
# 检查是否连续 4 次未掷出正面
if noCritStreakCount < 4:
# 同上文代码
# 同上文代码
# 同上文代码
输出结果如下图所示
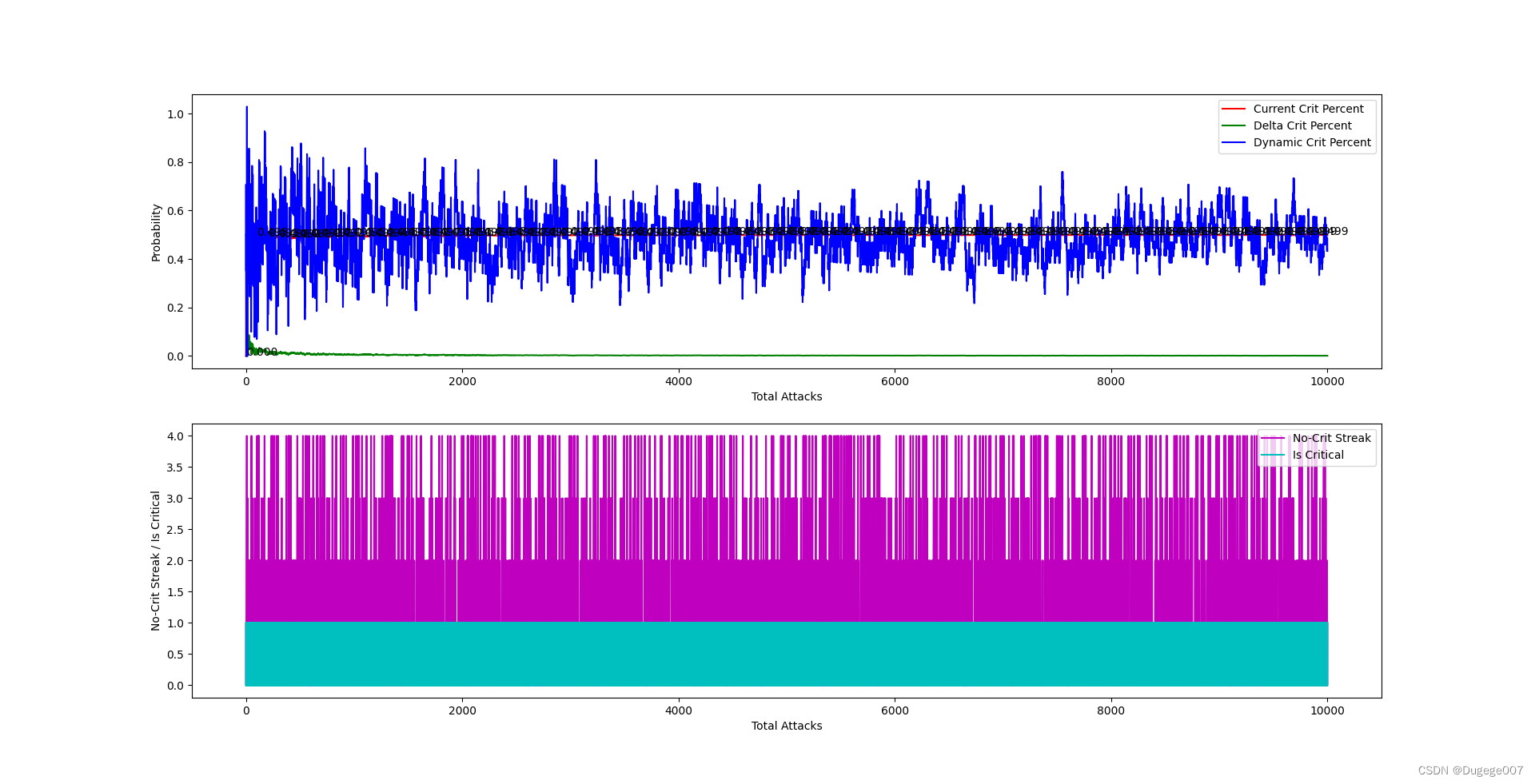
前 2000 次 如下
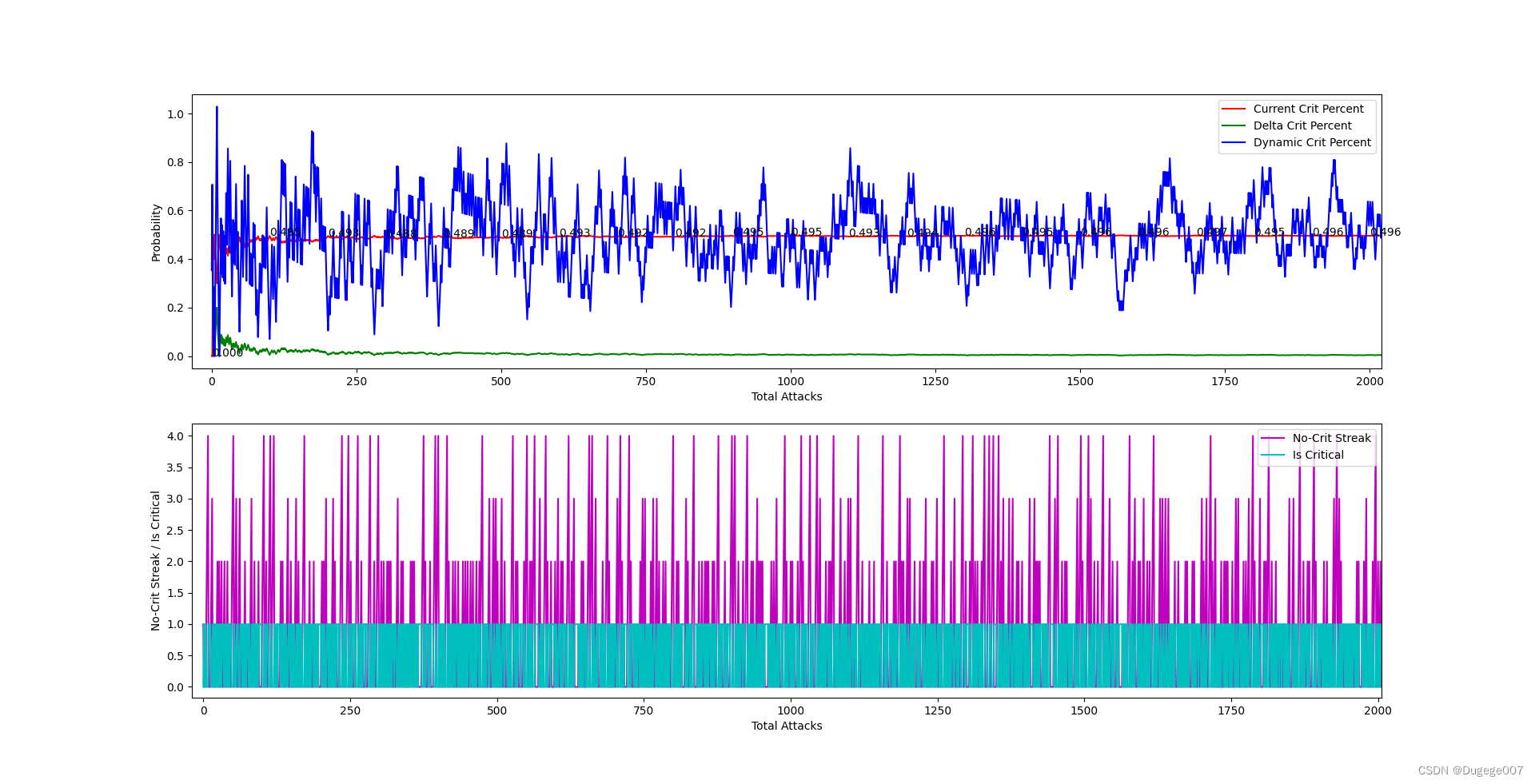
8000 ~ 10000 次 如下
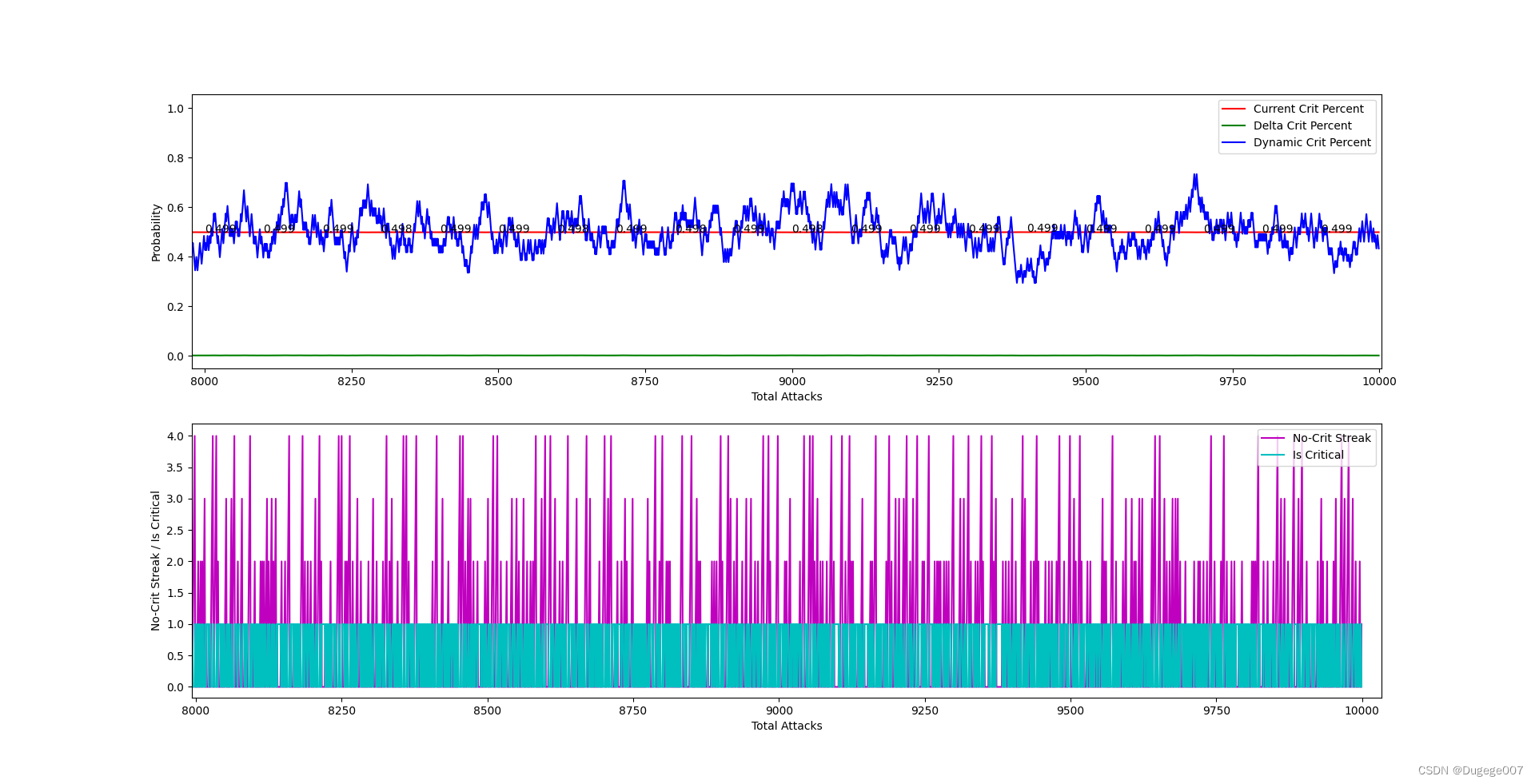
也基本符合预期。
掷骰子
再以掷骰子为例:每掷出 15 次至少有一次是 点数 1。
# 同上文代码
InitCritPercent = 0.166667
dynamicCritPercent = 0.166667
# 同上文代码
# 测试 10000 次
for i in range(10000):
# 同上文代码
# 检查是否连续 14 次未掷出正面
if noCritStreakCount < 14:
# 同上文代码
# 同上文代码
# 同上文代码
输出结果如下图所示
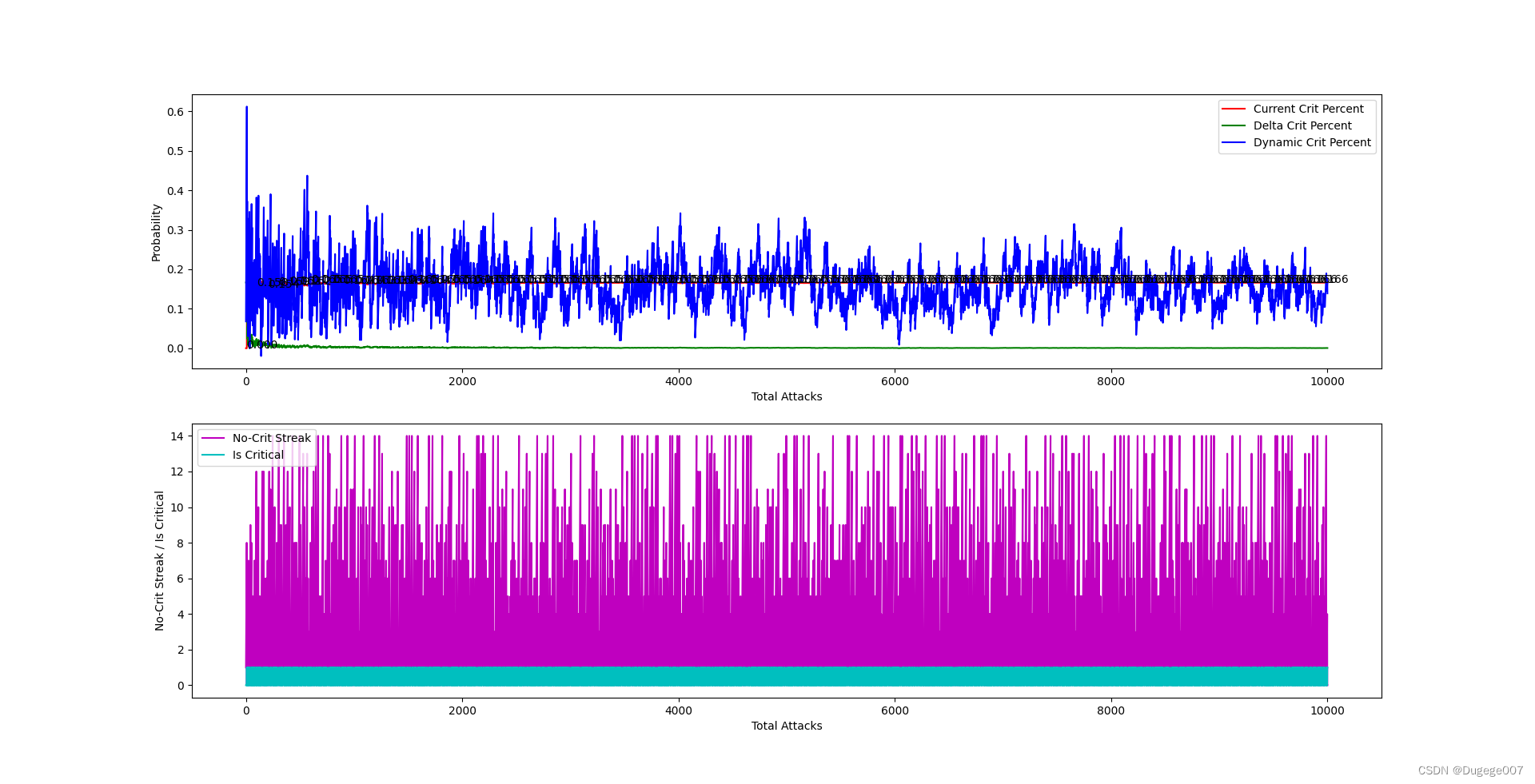
前 2000 次 如下
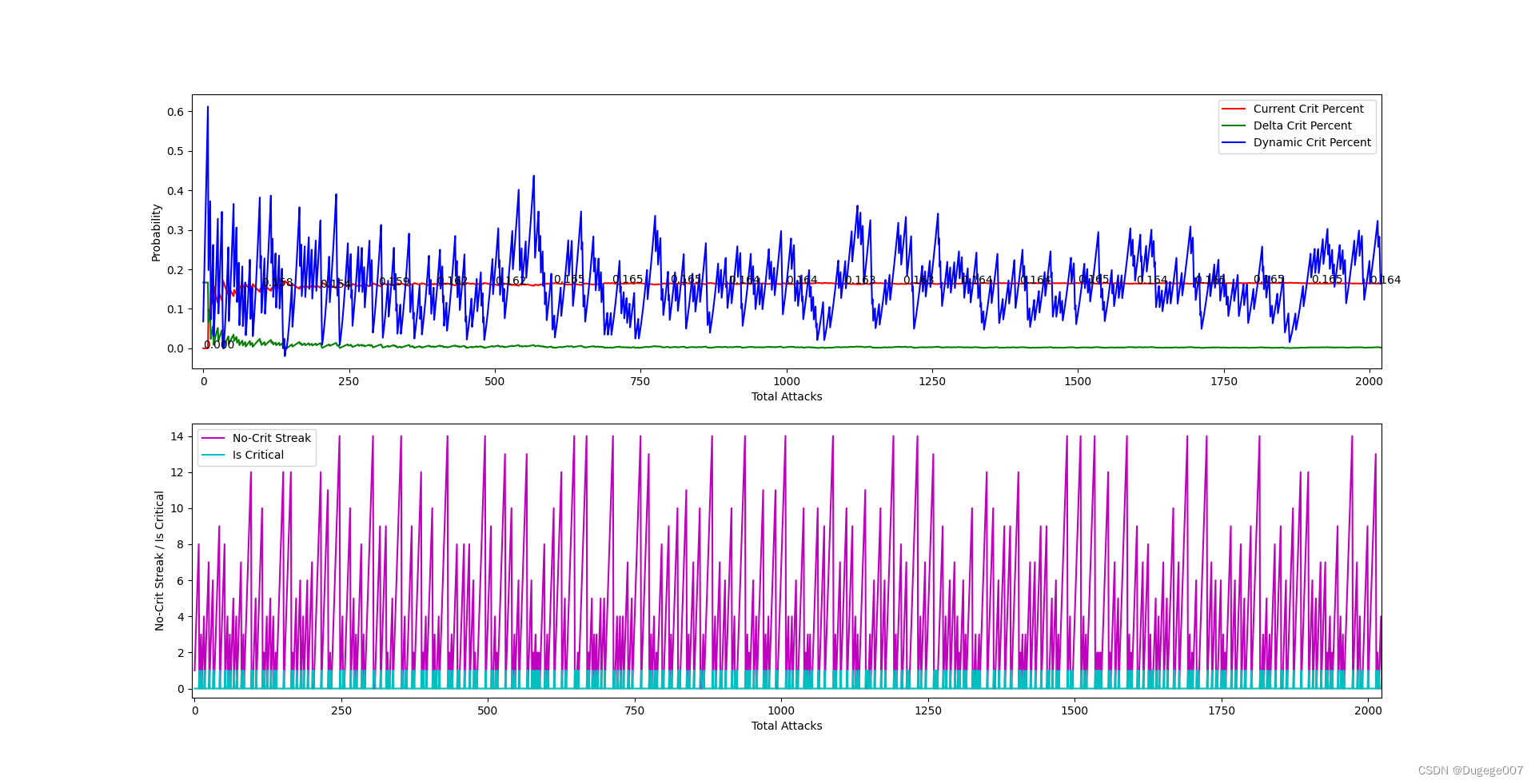
8000 ~ 10000 次 如下
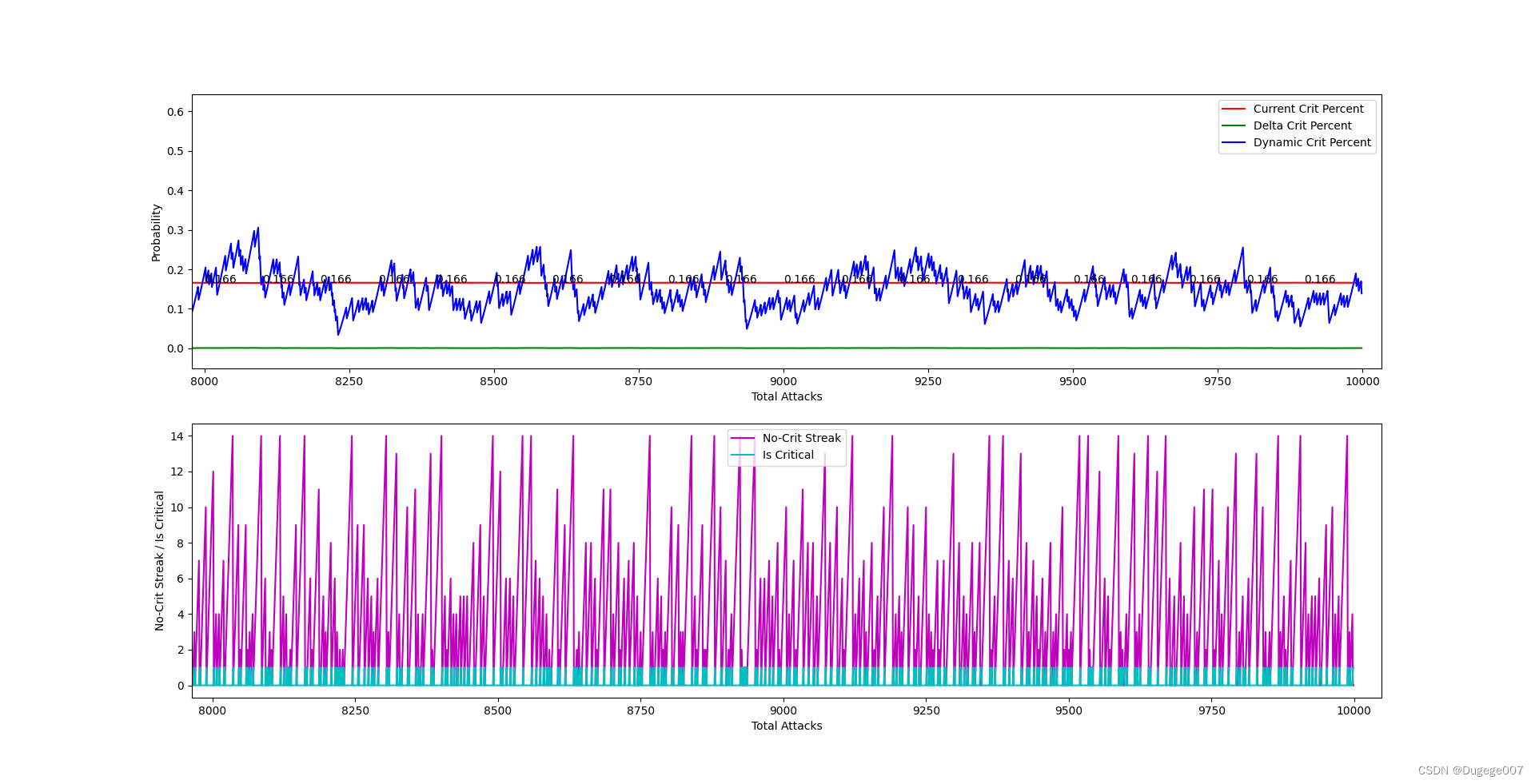
稳定发挥。
优化
目前“镜像修正”算法已经基本可用了,但是虽然叫“镜像”,却已经没有了镜像当初的样子。
不如就直接改名叫“动态平衡概率”算法好了…
算法优化
细心的朋友应该会发现,这套算法在一开始的概率会低于目标概率一些,并且逼近的速度还是慢了些。后期稳定性也没有想象中的高。
笔者目前能想到的继续优化的方式有三种:
1.分段修改 deltaCritPercent 的开根,类似LOD模型替换的感觉;
2.用 log 函数做系数,然后当次数达到一定值时直接 * deltaCritPercent 就可以了;
3.按目标概率的比例,给“总攻击次数”和“总暴击次数”设置较大的初始值。这样不用给 deltaCritPercent 开平方,就能得到一个较为满意的结果,也会相对高效一些。
笔者还没来得及测试性能,如果后续有相关优化会修改本文章,或者发一篇新文章。
关于判断次数
我们感觉到的小概率事件发生的概率通常在 5% 或 1% 以下,通过这两个标准,我们可以很轻松地得出“目标概率为 X 时,操作 N 次至少出现一次目标事件”中的N:
def find_optimal_N(p):
# 从 1 到 500
for i in range(1, 501):
if(1 - p) ** i <= 0.05:
return i
print(find_optimal_N(0.2))
print(find_optimal_N(0.5))
print(find_optimal_N(0.166667))
# 输出结果为:
# 14
# 5
# 17
所以当目标概率为 0.2、0.5、0.166667 时,N 比较合适的值为 14、5、17。
当目标概率小于 0.05 时,可以让if(1 - p) ** i <= 0.01:,或者更小。
结语
虽然本算法目前还有待优化,但已经足够应对一些游戏场景。
关于那多出的2.5%的问题,笔者会继续探索,直到找到满意的答案。
如果这篇文章能为你解决问题或带来新的启发,那我会感到非常荣幸!
对于已经在这个领域有丰富经验的大佬们,非常欢迎你们的建议或批评。这不仅能帮助我改进,也能让这篇文章更加完善,从而帮助到更多的人。
感谢你抽出宝贵的时间来阅读这篇文章,如果你觉得有用,也请不吝分享给更多需要的人。
再次感谢,期待我们在知识的海洋里再次相遇!



![2023年中国改性聚乙烯产能、产量及市场规模现状分析[图]](https://img-blog.csdnimg.cn/img_convert/8dc35a1941a21d7fdfa34cc75ab13618.png)
![[12 种安卓数据恢复方案] 最佳免费 Android 照片恢复工具榜单](https://img-blog.csdnimg.cn/img_convert/fd15a460a99b31013b28d5b2eb354bea.jpeg)