📝个人主页:@Sherry的成长之路
🏠学习社区:Sherry的成长之路(个人社区)
📖专栏链接:练题
🎯长路漫漫浩浩,万事皆有期待
文章目录
- 二叉搜索树的最近公共祖先
- 叉搜索树中的插入操作
- 删除二叉搜索树中的节点
- 总结:
二叉搜索树的最近公共祖先
235. 二叉搜索树的最近公共祖先 - 力扣(LeetCode)
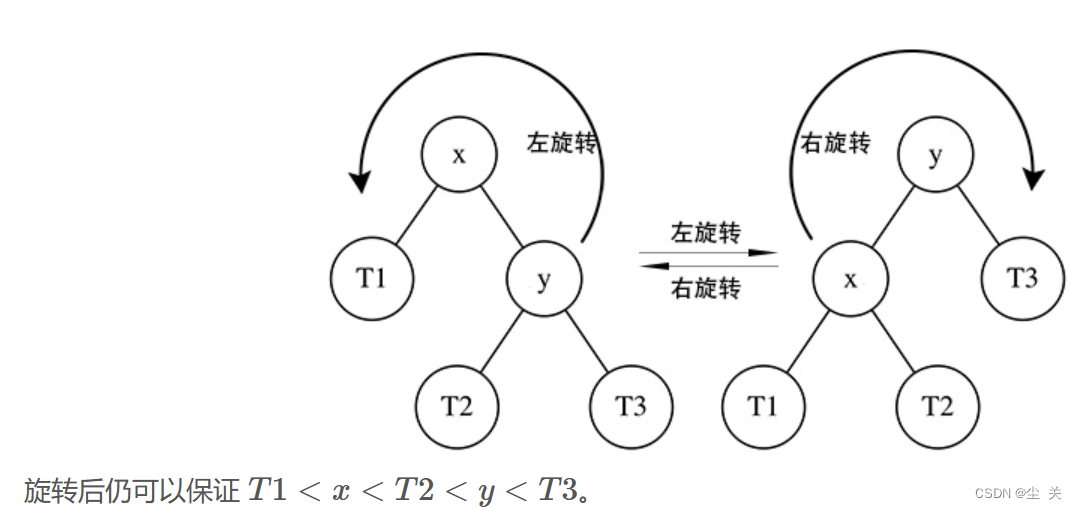
看了题解,发现这道题与上一期相似的题的区别是,普通二叉树的查找最近公共节点,我们需要从二叉树的底部向上面遍历处理节点,而二叉搜索树,由于它自身拥有特定的排列顺序的缘故,我们要从上到下顺序的遍历处理节点,这一点上处理节点的顺序是不同的。我们根据搜索树的特征,将我们要查找的节点对应的值,与现在处在的节点值作比较,如果要查找的值大那么向右子树寻找,如果小向左子树递归
class Solution {
public:
TreeNode* traversal(TreeNode* cur,TreeNode* p,TreeNode* q)
{
if(cur==NULL)
{
return cur;
}
if(cur->val>p->val&&cur->val>q->val)
{
TreeNode* left=traversal(cur->left,p,q);
if(left!=NULL)
{
return left;
}
}
if(cur->val<p->val&&cur->val<q->val)
{
TreeNode* right=traversal(cur->right,p,q);
if(right!=NULL)
{
return right;
}
}
return cur;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
return traversal(root,p,q);
}
};
代码比求普通二叉树略简短一些。递归通过对left和right的判断而看是否找到了p,q其中之一,向上返回,我们将处在p和q中间的第一次遇到的节点直接返回上去,因为第一次遍历到的那个p和q中间的节点一定处在p和q子树的中间节点,如果它再向左或者向右子树递归,那么就一定会错过p或者q中的其中一个。这就是为什么我们遇到数值在其中间直接返回,这也是根据了搜索树的特性。
叉搜索树中的插入操作
701. 二叉搜索树中的插入操作 - 力扣(LeetCode)
二叉搜索树中的插入操作,是略有理解难度的。起初在做这道题时,我们可能会被题目实例中的可以以多种答案提交而搞懵,有直接插入的,还有改变了二叉树结构插入进去的。这里我们需要明白,我们插入的任何节点都可以直接插入到该二叉搜索树的叶子节点处,也就是说不必要改变树的结构,因为改变树的结构的代码实现起来是有一些困难的。不理解为什么要插入的任何节点都可以在叶子节点插入的可以自行模拟一下。这里不必担心要插入的节点会和原二叉树某些节点值1相同,题目已经明确告诉了。
class Solution {
public:
TreeNode* parent;
void traversal(TreeNode* cur,int val)
{
if(cur==nullptr)
{
TreeNode* node=new TreeNode(val);
if(val>parent->val)
{
parent->right=node;
}
else
{
parent->left=node;
}
return;
}
parent=cur;
if(cur->val>val)
{
traversal(cur->left,val);
}
if(cur->val<val)
{
traversal(cur->right,val);
}
return;
}
TreeNode* insertIntoBST(TreeNode* root, int val) {
parent=new TreeNode(0);
if(root==nullptr)
{
root=new TreeNode(val);
}
traversal(root,val);
return root;
}
};
起初写代码时候,我是又自定义了一个void类型的函数,但是看了题解发现那样做很麻烦,直接在主函数上改动,是本题的最优解,当我们遍历到空的时候也就是找到了我们要插入的地点了,我们就直接原地创建一个节点然后返回上去,返回到上一层让上一层的节点链接我们要插入进去的节点即可。
class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
if(root==NULL){
TreeNode*node=new TreeNode(val);
return node;
}
if(root->val>val){
root->left=insertIntoBST(root->left,val);
}
if(root->val<val){
root->right=insertIntoBST(root->right,val);
}
return root;
}
};
这道题的向上递归逻辑就是,一层链接一层,由于我们没有改动二叉搜索树的结构,但是我觉得最好也要清楚,递归是如何一层一层向上返回的,它是每一次向上返回本层的节点,连接到上一层的left或者right处,当全部返回了之后,再把最开始的根节点root返回上去,作为返回值。
删除二叉搜索树中的节点
450. 删除二叉搜索树中的节点 - 力扣(LeetCode)
删除二叉树的节点面临着改变二叉树的结构,而无法避免。所以该类型题是较有难度的,删除二叉搜索的某节点,大致分为几种情况:要删除的节点并不在该二叉树中,删除的是叶子节点,删除的节点有左子树但是没有右子树,有右子树但没有左子树,最后一种情况是左右子树都有,其中最后一种是最复杂的。
找不到该节点我们可以直接向上返回,不对该二叉树做任何的改动,如果是叶子节点那么我们将null返回到上一层,让链接目标节点的节点某一方向指向空,这时候我们就直接把它从二叉树上取了下来,中间的两者,都是让上一层链接我们要删除的节点的不为空的子树部分,直接连接上去就可以了,避免都结构的改动。最后一种,我们需要向上一层返回的是:该节点右子树的最左子树链接要删除节点的左子树。因为我们要删除的节点的右子树节点一定都比我们的要删除的左子树节点值要大,而它右子树的最左侧子树的值应该是略大于要删除的节点,这样我们就只是在我们删除的节点的右子树的最左侧叶子节点处插入了一本来就有序的左子树,这样的改动最大限度的减小了结构处理的困难性。
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if(root==nullptr)
{
return root;
}
if(root->val==key)
{
if(root->left==nullptr&&root->right==nullptr)
{
delete root;
return nullptr;
}
else if(root->left==nullptr)
{
auto retNode=root->right;
delete root;
return retNode;
}
else if(root->right==nullptr)
{
auto retNode=root->left;
delete root;
return retNode;
}
else
{
TreeNode* cur=root->right;
while(cur->left!=nullptr)
{
cur=cur->left;
}
cur->left=root->left;
TreeNode* tmp=root;
root=root->right;
delete tmp;
return root;
}
}
if(root->val>key)
{
root->left=deleteNode(root->left,key);
}
if(root->val<key)
{
root->right=deleteNode(root->right,key);
}
return root;
}
};
判断部分略多了一些,递归部分很少,这道题的递归返回逻辑仍然是,将本层的节点返回给上一层,然后上一层再链接当前节点的树。
总结:
今天我们完成了二叉搜索树的最近公共祖先、二叉搜索树中的插入操作、删除二叉搜索树中的节点三道题,相关的思想需要多复习回顾。接下来,我们继续进行算法练习。希望我的文章和讲解能对大家的学习提供一些帮助。
当然,本文仍有许多不足之处,欢迎各位小伙伴们随时私信交流、批评指正!我们下期见~