300.最长递增子序列
/**
* @param {number[]} nums
* @return {number}
*/
var lengthOfLIS = function(nums) {
let dp = Array(nums.length).fill(1);
let result = 1;
for(let i = 1; i < nums.length; i++) {
for(let j = 0; j < i; j++) {
if(nums[i] > nums[j]) {
dp[i] = Math.max(dp[i], dp[j]+1);
}
}
result = Math.max(result, dp[i]);
}
return result;
};
思路
当前下标i的递增子序列长度,其实和i之前的下表j的子序列长度有关系
- dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度
- 递推方程 :if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值。 - dp[i]的初始化
每一个i,对应的dp[i](即最长递增子序列)起始大小至少都是1.

674. 最长连续递增序列
/**
* @param {number[]} nums
* @return {number}
*/
var findLengthOfLCIS = function(nums) {
let m=1
let temp=1
for(let i=1;i<nums.length;i++){
if(nums[i]>nums[i-1])
temp++
else {
temp=1
}
m=Math.max(m,temp)
}
return m
};
第一想法
如上,贪心
dp做法
let dp = new Array(nums.length).fill(1);
//dp[i]:以下标i为结尾的连续递增的子序列长度为dp[i]
for(let i = 0; i < nums.length - 1; i++) {
if(nums[i+1] > nums[i]) {
dp[i+1] = dp[i]+ 1;
}
}
return Math.max(...dp);
718. 最长重复子数组
/**
* @param {number[]} A
* @param {number[]} B
* @return {number}
*/
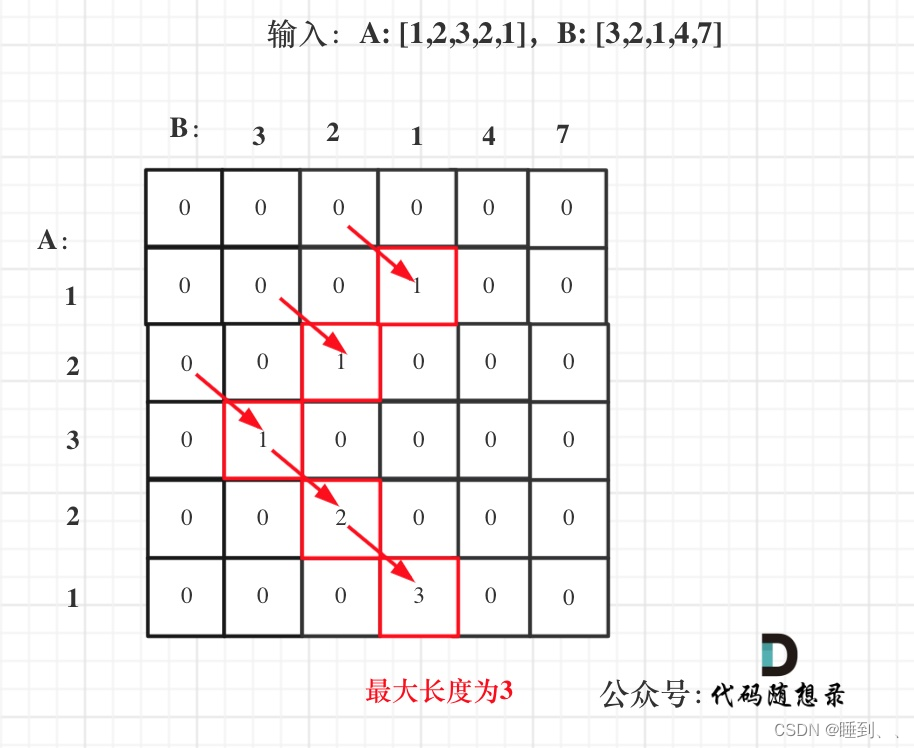
var findLength = function(A, B) {
// A、B数组的长度
const [m, n] = [A.length, B.length];
// dp数组初始化,都初始化为0
const dp = new Array(m + 1).fill(0).map(x => new Array(n + 1).fill(0));
// 初始化最大长度为0
let res = 0;
for (let i = 1; i <= m; i++) {
for (let j = 1; j <= n; j++) {
// 遇到A[i - 1] === B[j - 1],则更新dp数组
if (A[i - 1] === B[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
}
// 更新res
res = dp[i][j] > res ? dp[i][j] : res;
}
}
// 遍历完成,返回res
return res;
};
思想
- 以下标i - 1为结尾的A,和以下标j - 1为结尾的B,最长重复子数组长度为dp[i][j]。
- 递推公式
即当A[i - 1] 和B[j - 1]相等的时候,dp[i][j] = dp[i - 1][j - 1] + 1; - 初始化
举个例子A[0]如果和B[0]相同的话,dp[1][1] = dp[0][0] + 1,只有dp[0][0]初始为0,正好符合递推公式逐步累加起来。
滚动数列
dp[i][j]都是由dp[i - 1][j - 1]推出。那么压缩为一维数组,也就是dp[j]都是由dp[j - 1]推出。
也就是相当于可以把上一层dp[i - 1][j]拷贝到下一层dp[i][j]来继续用。
for (int i = 1; i <= A.size(); i++) {
for (int j = B.size(); j > 0; j--) {
if (A[i - 1] == B[j - 1]) {
dp[j] = dp[j - 1] + 1;
} else dp[j] = 0; // 注意这里不相等的时候要有赋0的操作
if (dp[j] > result) result = dp[j];
}
dp[i][j]为 以下标i为结尾的A,和以下标j 为结尾的B,最长重复子数组长度?
如果定义 dp[i][j]为 以下标i为结尾的A,和以下标j 为结尾的B,那么 第一行和第一列毕竟要进行初始化,如果nums1[i] 与 nums2[0] 相同的话,对应的 dp[i][0]就要初始为1, 因为此时最长重复子数组为1。 nums2[j] 与 nums1[0]相同的话
困难
收获
1
/**
* @param {number[]} nums
* @return {number[]}
*/