(一) 基础补充
二叉搜索树(BST)
定义:
二叉搜索树(Binary Search Tree),简写BST,是满足某些条件的特殊二叉树。任何一个节点的左子树上的点,都必须小于当前节点。任何一个节点的右子树上的点,都必须大于当前节点。任何一棵子树,也都满足上面两个条件。即对于根节点,左子树中所有节点的值 < 根节点的值 < 右子树中所有节点的值。另外,在二叉查找树中,是不存在重复节点的。本文中AVL 树和二叉搜索树有很多共同点, AVL 树只是增加了自平衡的部分。
数据结构--- 树_尘 关的博客-CSDN博客 具体请看
(二)解析AVL
AVL来源
1962年,G. M. Adelson-Velsky 和 Evgenii Landis 在其论文 "An algorithm for the organizational of information" 中首次介绍了 AVL 树这种数据结构。AVL 树作为最早出现的自平衡二叉搜索树,其主要特点是任意节点的两个子树的高度最大差别为1,因此它也被称为高度平衡树。在 AVL 树上执行查找、插入和删除的平均和最坏情况下的时间复杂度都是O(log n)。同时,添加和删除节点时可能需要进行一次或多次的树旋转来保持平衡。—— 某科
AVL树是高度平衡的二叉树。它的特点是: AVL树中任何节点的两个子树的高度最大差别为1。
————吾言
为什么会有AVL
在查找元素时,二叉搜索树的速度明显优于普通二叉树。但是,如果二叉搜索树不平衡,搜索速度将受到严重影响。
以下数字:8, 15, 24, 29, 32, 56为例,考虑下面的三种不同的树形结构示例。就搜索效率而言,第二棵树的效率是最高的,第一棵树次之,而第三棵树效率最低。假如我们想查找数字8,第二棵树只需3次比较,第一棵树需要4次,而第三棵树需要6次。事实上,第三棵树基本上已经变成了一个链表结构。

综上所言,为了提高二叉搜索树的搜索效率,我们应该尽量减少树的深度————减少左右子树的高度差是一种有效的方法。当任何节点的左右子树高度差不超过1时,这个二叉搜索树可以被认为是平衡的。
关于AVL树的一些概念
高度
高度是节点到最远的叶子节点的距离。(千人千言,但终殊途同归,本文采用)
平衡因子
AVL 树使用节点中的高度(height)属性测量节点是否平衡。
如图,AVL树:

旋转
树旋转是对二叉树的一种操作,不影响元素的顺序(二叉搜索树,但会改变树的结构。
一般有两种旋转方式:
- 左旋转,逆时针旋转
- 右旋转,顺时针旋转
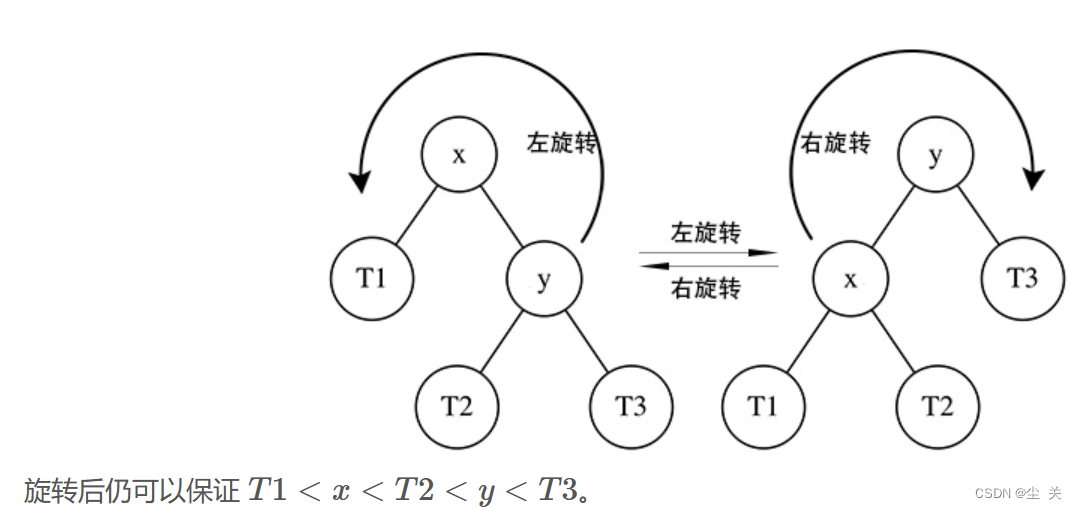
,孩子和孙子方向一致(都是左或者都是右),那么就简单一次旋转就能整理好,如果方向不一致(一左一右),先在孩子节点上把孙子节点转到同一方向上,然后再在父节点上按照刚刚方向一致的情况处理。
剖析——AVL的底层思维(重点)
AVL Tree Visualzation (usfca.edu) ——看文章里面有实现的动画,自个玩玩呗。