yolov5中的位置损失到底有哪些？

news2024/11/15 20:31:05

1.IOU loss

2.GIOU

3.DIOU和CIOU

5.SIOU

6.EIOU

7.WIOU

8.MPDIOU

别人问目标检测有几个损失函数？

我答：三个。

别人笑了笑。

我问：难道我说记错了？

别人说：是的，你记错了。

我说：哦。

经常糊里糊涂的我竟然没有反驳。

今天就理一理yolov5的损失，并重点讲一下其中的位置损失。

------------------------

yolov5有三个损失函数：分类损失，位置损失，置信度损失

总体的损失为以上三者的加权相加，通过改变权值可以调整三者损失的关注度。

证据：utils/loss.py line240

其中的参数设置：

data/hyps/hyp.scratch.yml

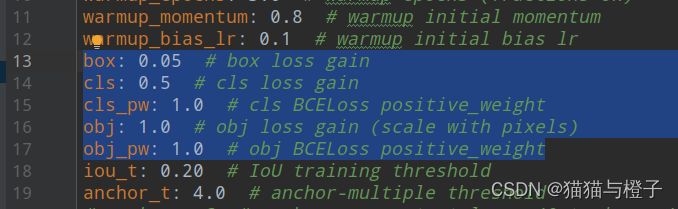
分类损失：

通常对于分类任务，输出的标签是互斥的。yolov5中是对每一个类别预测结果使用二元交叉损失。

位置损失：

边界框预测是目标检测中最主要的任务之一，目标检测中想要框出检测到的目标，就需要通过对边界框所在位置数据的预测。

目标损失：

使用交叉熵损失作为目标损失，有效的区分背景和前景；

--------------------

对于位置损失，目前的发展顺序：

IOU -》DIOU -》CIOU -》SIOU -》EIOU -》WIOU -》MPDIOU

1.IOU loss

论文：《UnitBox: An Advanced Object Detection Network》

链接：https://arxiv.org/pdf/1608.01471.pdf

之前用的回归损失存在问题：

但该方式还存在两个问题（来自论文《Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression》中的观点，https://arxiv.org/pdf/1902.09630.pdf）：

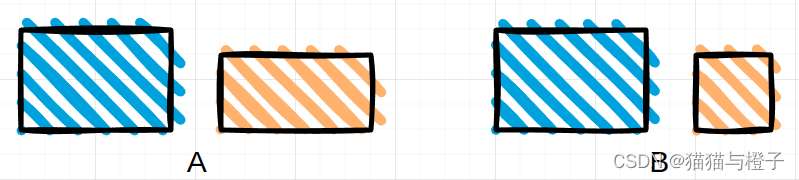
1.a图和b图中2图都没有重叠，但是使用l2loss无法反应出A和B之间的距离（C与D之间的距离）；

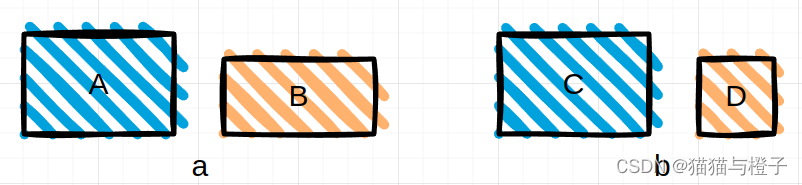
2.预测框与gt框之间不能完全反映重叠度的好坏。

iou loss相比于l2 loss收敛性更好，ROC曲线指标也更好（参考：https://arxiv.org/pdf/1608.01471.pdf）

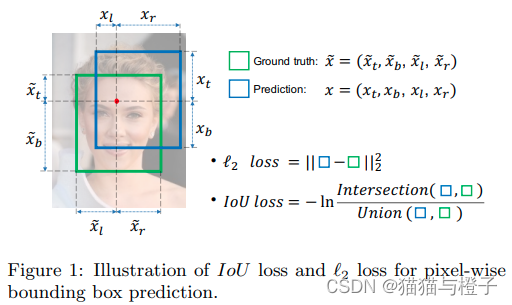
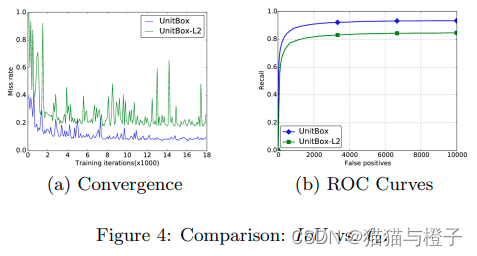
该方法存在缺陷：

1.当真实框和预测框完全不重叠时，因为其损失都为 1，则无法反映预测框离真实框的远近；

2.当真实框包含预测框，且真实框与预测框的大小固定时，其 IoU 很定为预测框与真实框面积的比值，则无论预测框在真实框中的哪个位置，损失都不变。

2.GIOU

论文：《Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression》

链接：https://arxiv.org/pdf/1902.09630.pdf

其中C就是包含两个框的最小矩形外框，GIOU计算中分子表示C中除了A和B并集的剩下部分。

损失函数：

$L_{giou} = 1-giou$

3.DIOU和CIOU

论文：《Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression》

链接：https://arxiv.org/pdf/1911.08287.pdf

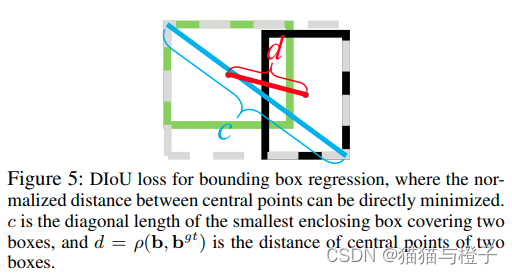
作者认为好的检测回归损失应该需要考虑三个方面：预测框和GT框的重叠度、预测框和GT框的中心点距离、预测框和GT框各自的长宽比一致性。于是在iou loss的基础上提出了DIOU loss：引入了预测框和GT框中心点的距离。在DIOU loss的基础上提出了CIOU loss：引入了预测框的长宽比和GT框的长宽比。

损失函数：

将检测框和GT框之间的中心距离加入loss可以在两框不想交的时候指引预测。解决了大框包小框时的问题：

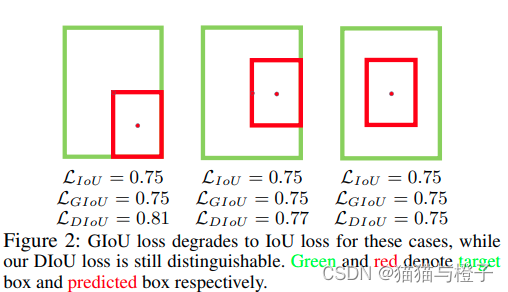
第三种类型的图，iou中加入了中心距离后，得到的DIOU的loss最小，这是很合理的。

作者将diou加入到nms替换iou，当中心点距离近到一定范围的多数情况下表示的是同一个目标，而中心点距离过远即使二者iou超过阈值有可能是遮挡和被遮挡的两个目标。如下图：

上图中，采用diou nms将被遮挡的目标释放出来了。

5.SIOU

论文：《SIoU Loss: More Powerful Learning for Bounding Box Regression Zhora Gevorgyan》

链接：https://arxiv.org/pdf/2205.12740.pdf

SIOU在考虑重叠区域，距离和长宽，还考虑了2个框的角度问题。当预测框和真实框不想交时，如何加快收敛速度，作者认为真实框与预测框框之间的方向，导致收敛速度较慢，角度损失定义如下：

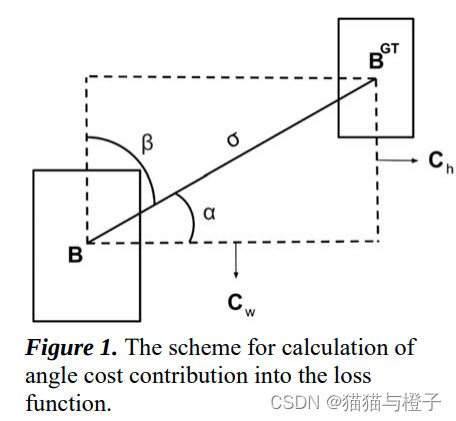
Ch为真实框和预测框中心点的高度差，δ为真实框和预测框中心点的距离。

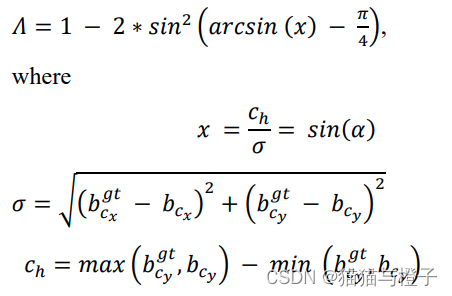
$(b_{C_{_{x}}}^{gt},b_{C_{_{y}}}^{gt})$ 为真实框中心坐标 $(b_{C_{_{x}}},b_{C_{_{y}}})$ 为预测框中心坐标，可以注意到当 $\alpha$ 为 $\frac{\pi }{ 2}$ 或0时，在训练过程中若 $\alpha<\frac{\pi }{4}$ ,则最小化 $\alpha$ ，否则最小化 $\beta$ 。

距离代价（Distance cost）：考虑GT框和预测框之间的距离

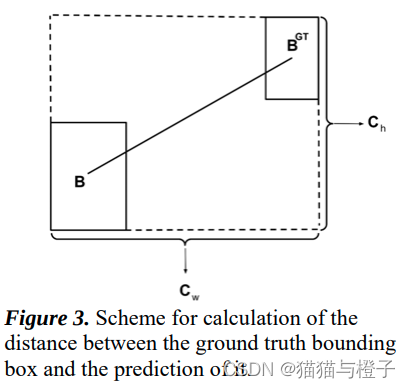
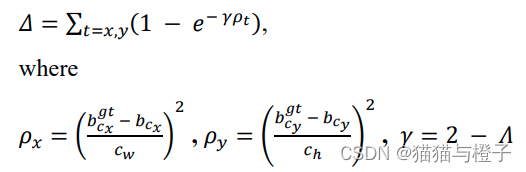
在计算Λ时，当两个框近乎平行的时候，Λ趋近于0，这样计算出来两框之间的角度距离接近0，此时γ的值接近2，则两框之间的距离对于整体loss贡献变少。当两个框的角度在45时，Λ趋近于1，此时γ的值接近1，则两框之间的距离应该被重视，需要占更多的loss。

形状代价（Shape cost）：考虑两个框之间的长宽比，是通过计算两框之间的宽只差和两个框之间最大宽之比来定义的。

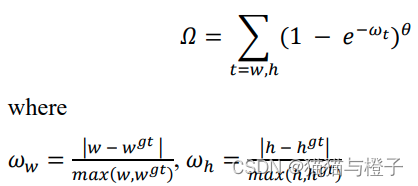
重叠区域考虑：重叠区域考虑其实就是普通的IOU。

最后的整体loss公式：

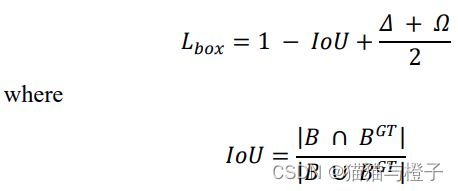
6.EIOU

论文：《Focal and Efficient IOU Loss for Accurate Bounding Box Regression》

链接：https://arxiv.org/pdf/2101.08158.pdf

作者认为ciou loss对于长宽比的加入loss的设计不太合理，于是将ciou loss中反应长宽比一致性的部分替换成了分别对于长和宽的一致性loss，形成了eiou loss；其次，大多数损失函数忽略了正负样本不平衡的问题，即大量与目标框重叠面积较小的预测框在最终的 bbox 优化中占用了绝大部分的贡献。

公式定义：

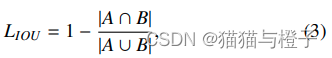
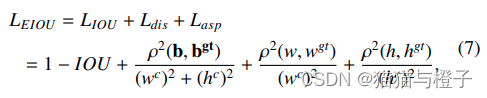
其中，Wc和hc是预测边界框与真实框的最小外接矩形的宽度和高度，p是两点之间的欧氏距离。

7.WIOU

论文：《Wise-IoU: Bounding Box Regression Loss with Dynamic Focusing Mechanism》论文链接：https://arxiv.org/pdf/2301.10051.pdf

使用IOU损失的时候，当边界框没有重叠的时候，反向传播的梯度消失了。本文就是解决这个问题。

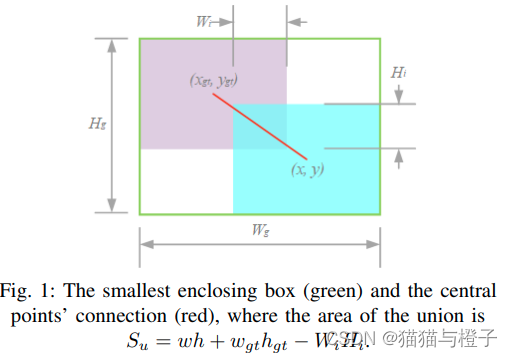
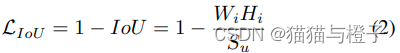
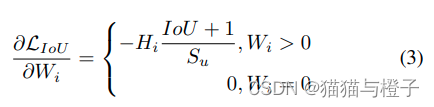
作者考虑使用构造了惩罚项Ri来解决这个问题。加入惩罚项的公式：

DIOU将惩罚项定义为中心点连接的归一化长度：

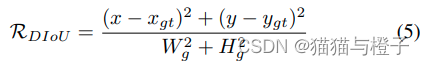
EIoU 在此基础上加大了对距离度量的惩罚力度，其惩罚项定义为：

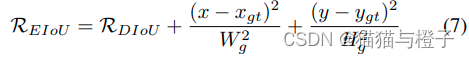
Complete-IOU

在RDIOU的基础上，CIOU增加了对纵横比一致性的考虑：

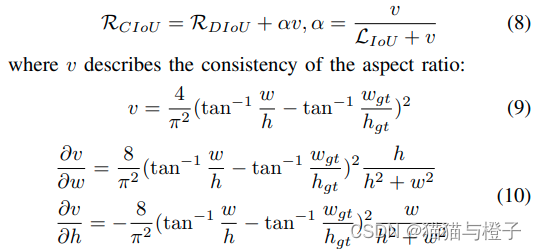
其中 $\nu$ 反向传播的梯度满足 $\frac{\partial \nu }{\partial h }=-\frac{\omega }{h}\frac{\partial \nu }{\partial \omega }$ ,也就是v不可能为预测框的宽高提供同号的梯度。在前文对DIoU的分析中可知DIoU会产生负梯度 $\frac{\partial R_{DIoU}}{\partial W_{g}}$ ,当这个负梯度与 $\frac{\partial L_{IoU}}{\partial W_{g}}$

正好抵消时，会导致预测框无法优化。而CIoU对纵横比一致性的可以优化该问题。

（略，后续补充完整）... ...

8.MPDIOU

论文：《MPDIoU: A Loss for Efficient and Accurate Bounding Box Regression》

链接：https://arxiv.org/pdf/2307.07662.pdf

目的：大多数的边界框回归损失函数在不同预测结果下具有相同的值，这降低了边界框回归的收敛速度和准确性。

所以作者提出了以下的算法：

def bbox_mpdiou(box1, box2, x1y1x2y2=True, mpdiou_hw=None, grid=None, eps=1e-7):
    # Returns the IoU of box1 to box2. box1 is 4, box2 is nx4
    box2 = box2.T
    box1[:2] += grid
    box2[:2] += grid

    # Get the coordinates of bounding boxes
    if x1y1x2y2:  # x1, y1, x2, y2 = box1
        b1_x1, b1_y1, b1_x2, b1_y2 = box1[0], box1[1], box1[2], box1[3]
        b2_x1, b2_y1, b2_x2, b2_y2 = box2[0], box2[1], box2[2], box2[3]
    else:  # transform from xywh to xyxy
        b1_x1, b1_x2 = box1[0] - box1[2] / 2, box1[0] + box1[2] / 2
        b1_y1, b1_y2 = box1[1] - box1[3] / 2, box1[1] + box1[3] / 2
        b2_x1, b2_x2 = box2[0] - box2[2] / 2, box2[0] + box2[2] / 2
        b2_y1, b2_y2 = box2[1] - box2[3] / 2, box2[1] + box2[3] / 2
    
    # Intersection area
    inter = (torch.min(b1_x2, b2_x2) - torch.max(b1_x1, b2_x1)).clamp(0) * \
            (torch.min(b1_y2, b2_y2) - torch.max(b1_y1, b2_y1)).clamp(0)

    # Union Area
    w1, h1 = b1_x2 - b1_x1, b1_y2 - b1_y1 + eps
    w2, h2 = b2_x2 - b2_x1, b2_y2 - b2_y1 + eps
    union = w1 * h1 + w2 * h2 - inter + eps

    iou = inter / union
    d1 = (b2_x1 - b1_x1) ** 2 + (b2_y1 - b1_y1) ** 2
    d2 = (b2_x2 - b1_x2) ** 2 + (b2_y2 - b1_y2) ** 2
    return iou - d1 / mpdiou_hw - d2 / mpdiou_hw  # MPDIoU

注：以上是部分信息记录，没有详细讲述，不喜勿喷。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1084616.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！