1、稳定性分析

2、动态品质的求取

3、稳定误差计算

典型输入信号：

1、抛物线函数(等加速度阶跃函数)

2、单位阶跃函数

3.斜坡函数

A=1,是单位阶跃函数1(t)

4.脉冲函数

A=0 记为  

动态过程和稳态过程

超调量：（系统最大值-系统稳态值）/系统稳态值

线性常微分方程的通解=齐次方程通解+非齐次方程任一特解。

单位阶跃响应

r(t)=1  

(化成标准形式)

单位斜坡响应

r(t)=t       

(标准式：)

单位脉冲响应

R(s)=1

拉式反变换

线性定常系统 

系统对某信号导数的响应等于对该信号响应的导数。

系统对某信号积分的响应等于对该信号响应的积分。

二阶系统的暂态响应

二阶系统的单位阶跃响应

1、欠阻尼   

输入信号的拉氏变换，*传递函数=C(s).然后将输出进行拉斯反变换。

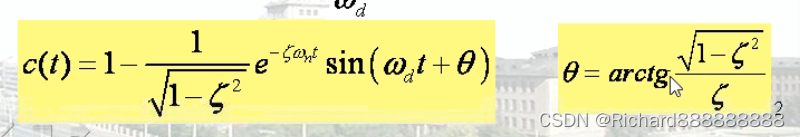
输出逐渐减小，但减小的过程中，逐渐震荡。

欠阻尼系统加入单位阶跃信号，输出的响应。

如下是响应曲线

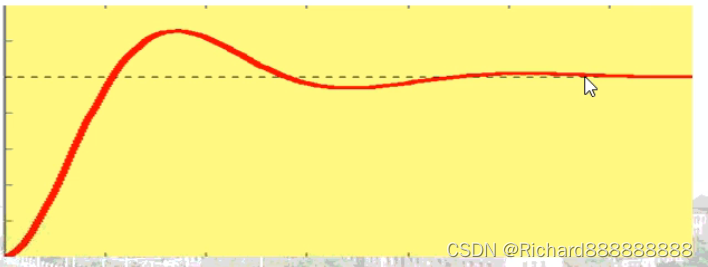
2、无阻尼系统 是欠阻尼系统的一个特例。

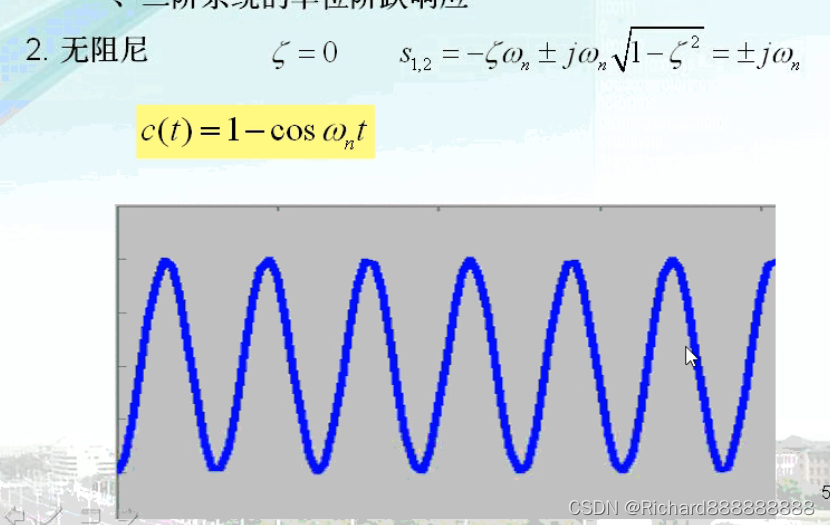
无阻尼系统是一个震荡的，最低点是0，最高点2的，加入阶跃信号的话，做等幅震荡。

3。临界阻尼。

是一个实数。

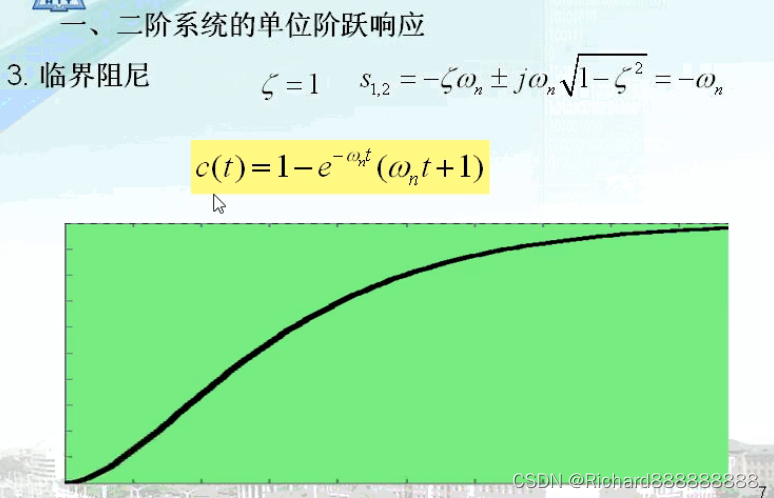
过阻 尼系统 

过阻 尼情况，加入阶跃信号时的图

性能指标：

上升时间

峰值时间 

最大超调量 

调整时间

最佳阻 尼比：超调量小，上升时间短。

二阶系统的暂态响应

如何得出的。

线性系统的稳定性

对于线性系统如果它是小范围稳定的，那它大范围肯定也是稳定的。

非线性是小范围稳定，大范围不稳定。

当初始偏差必须充分小时，系统才稳定，小偏差

范围内的稳定。

不管初始偏差有多大，系统总稳定。

在满足稳定条件下，当t——>无穷时，系统输出

重新回到原平衡点，如原平衡点为0时，渐近稳定。

是个复数，有实部和虚部组成。

当的实部<0时，输入趁近于1，系统稳定。

当系统所有特片根实部均为负(极点在S平面左半部），系统稳定。

只要有一个特征根实部为正(极点在S平面右半部),系统稳定。

有一个为零的特征根，或有一对在虚轴上的根——（共轭虚根）——系统临界稳定。

劳斯——赫尔判据

一种由特征方程的系数来判定系统稳定性的代数方法

如果系统稳定的话，特征根的实部就应该是负的，极点是负，根与系数的关系，由系数去判

定根的实部的正负。

系数首先要同号才有可能稳定，

如下，符号不同，所以是不稳定的。

如下，符号相同，但s一次方这一项缺失，所以也是不稳定的

下面是不一定， 不能说它是稳定的，也不能说它是不稳定的。不确定。

劳斯判据

第一步要列劳斯表

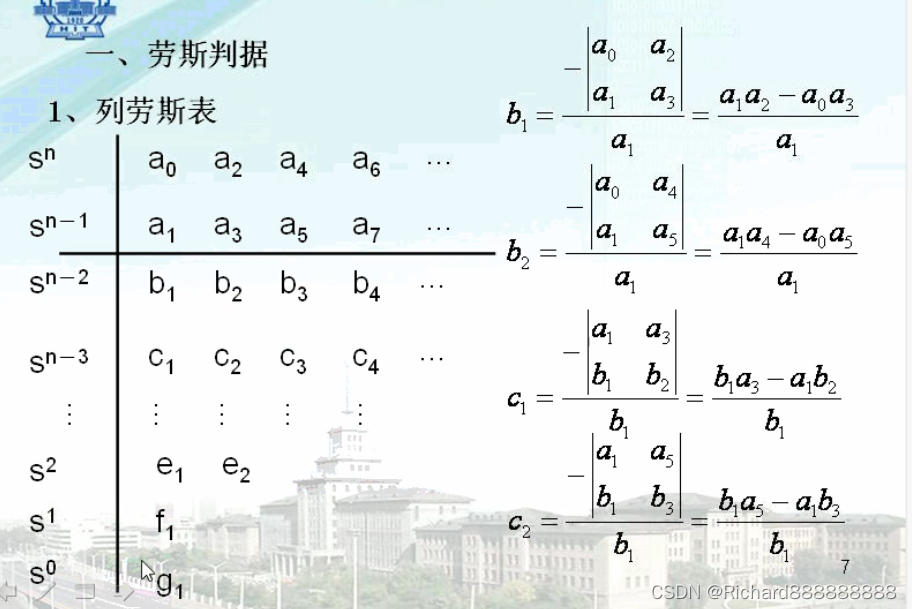
列劳斯表举例

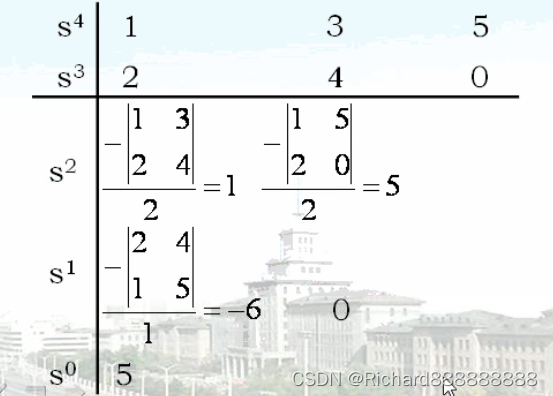
2.第二步，通过劳斯表第一烈的系数判断根的情况。

(1)第一列所有系数均不为零。

系统极点实部为正数根的数目等于劳斯表中第一列系数符号改变的次数。

如上图，第一列，符号全是正的，没有改变，说明右部s平面没有极点，说明系统稳定。

如上图，系数是同号的，不缺相，但劳斯表的第一项有变相，说明右边有极点，

所以不稳定。

-1/2改变了一次，9，又改变成正号，说明改变了两次，有两个正数根。

（2）某行第一列系数等于0，而其余项中某些项不等于零或没有其余项，用一

个很小 的正数代替为零的一项。

上面的系数符号与下面的系数符号相同——有一对虚根存在。

上面的系数符号与下面的系数符号相反——有一位于右半S平面的根。 

第一列系数符号改变----不稳定。

第一列系数符号不变----临界稳定。

概括以上的描述：

一旦第一列某一系数等于0，要么是不稳定，要么就是临界稳定，都属于不稳定系统。

举例说明：

如上图，第一列s1是0，则用代替。

(3)某一行所有各项系数均为零

存在一些大小相等，符号相反的实数和(或)一些共轭虚数极点。

如果某一行系数全部为零，则由上一行构造辅助方程，然后求导，将系数代替。

第一列系数符号改变——不稳定

第一列系数符号不变——临界稳定

举例说明

s5,s4行，得出第三行的系数全部是0，所以构造辅助方程，求导后，将

系数填入s3行，继续向下求。

也可以通过求辅助方程的特征根，如下，所求得s的正实部大于0，所以不稳定。

辅助多项式的次数表示特征根中数值相同，符号不同的根的数目。

赫尔维茨判据

一定是n行n列的。

判据:系统稳定的充分必要条件是在的情况下，上述行列式的各阶主子式大于零，

即。 

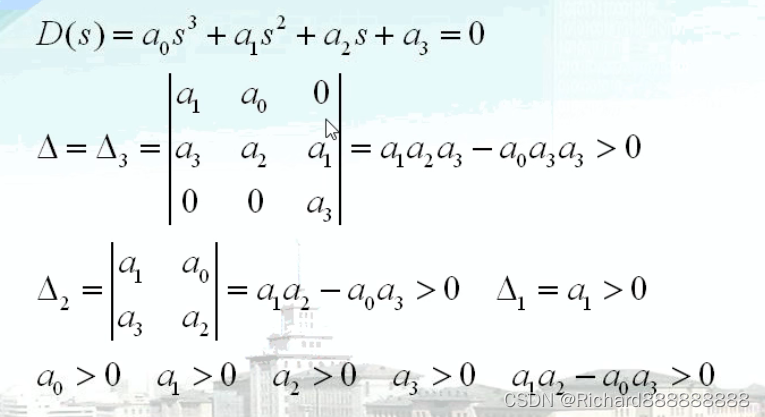
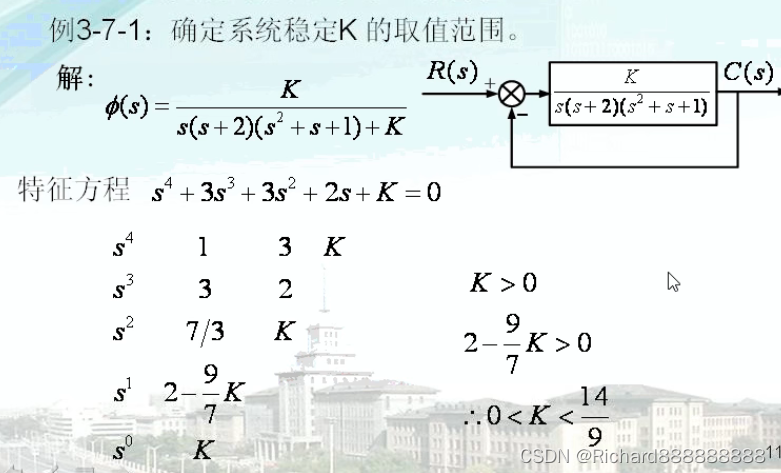
得到传递函数

要判断系统是否稳定，就要知道闭环极点在s平面的哪个位置。

因为求高阶方程很复杂，可以用劳斯判据。

稳态误差的定义

输入信号-主反馈信号。

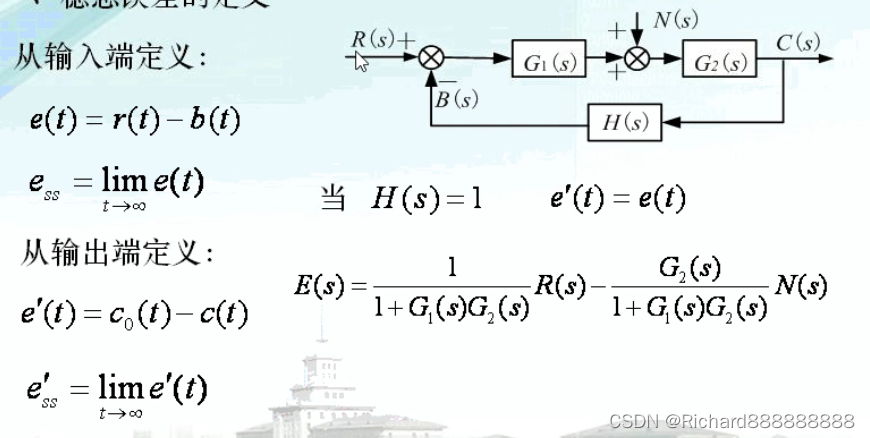
如上图的误差怎么计算

因为反馈是1，所以输入信号-输出信号=误差

简化后

减小误差的方式：

1、增加K

2、增加串联积分环节个数