来源:力扣(LeetCode)
描述:
给你 nums ,它是一个大小为 2 * n 的正整数数组。你必须对这个数组执行 n 次操作。
在第 i 次操作时(操作编号从 1 开始),你需要:
-
选择两个元素
x和y。 -
获得分数
i * gcd(x, y)。 -
将
x和y从nums中删除。
请你返回 n 次操作后你能获得的分数和最大为多少。
函数 gcd(x, y) 是 x 和 y 的最大公约数。
示例 1:
输入:nums = [1,2]
输出:1
解释:最优操作是:
(1 * gcd(1, 2)) = 1
示例 2:
输入:nums = [3,4,6,8]
输出:11
解释:最优操作是:
(1 * gcd(3, 6)) + (2 * gcd(4, 8)) = 3 + 8 = 11
示例 3:
输入:nums = [1,2,3,4,5,6]
输出:14
解释:最优操作是:
(1 * gcd(1, 5)) + (2 * gcd(2, 4)) + (3 * gcd(3, 6)) = 1 + 4 + 9 = 14
提示:
- 1 <= n <= 7
- nums.length == 2 * n
- 1 <= nums[i] <= 106
方法:状态压缩 + 动态规划
思路与算法
首先题目给出一个长度为 m = 2 × n 的正整数数组 nums,现在我们需要对这个数组进行 n 次操作——在第 i 次操作(操作编号从 1 开始),我们需要:选择两个元素 x 和 y,并得到分数 i × gcd(x, y),其中 gcd(x, y) 为 x 和 y 的最大公约数,然后把 x 和 y 从 nums 中删除。现在我们需要求进行 n 次操作后能获得的最大分数。
因为 1 ≤ n ≤ 7,所以我们可以用一个整数 s 来表示数组 nums 中未删除的数字状态——若数字 s 的二进制串从右往左的第 i 位为 1 则说明原数组中的第 i 位未被删除,否则表示被删除。然后我们设 dp[i] 表示对于未删除的数字状态为 i 时,我们往下进行操作能获得的最大分数,因为每次操作都需要删除两个元素,所以对于未删除的数字有奇数个的状态为非法状态,我们可以不做处理。那么我们思考如果进行状态转移——然后对于每个存在偶数个未删除数字的状态 s,假设其中有 ts 个未删除的数字,那么我们需要进行 ts / 2 次操作将全部数字删除。那么我们枚举第 ts / 2 次操作删除的两个元素可以得到:
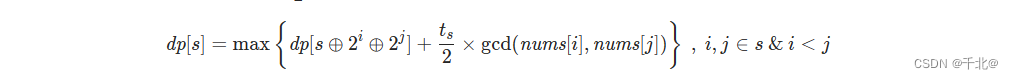
其中 s ⊕ 2i ⊕ 2j 表示从状态 s 中删除元素 nums[i] 和 nums[j] 的状态,gcd(nums[i], nums[j]) 表示 nums[i] 和 nums[j] 的最大公约数,为了避免重复运算每一对数字的最大公约数,我们可以在「动态规划」前对数组中的每一对数字的最大公约数进行预处理操作。当没有剩下的数字时,即 s = 0 时,我们不能继续往下操作,此时能获得的分数为 dp[0] = 0。然后我们可以「自底向上」来计算每一个状态,最后我们返回 dp[2m − 1] 即可。
代码:
class Solution {
public:
int maxScore(vector<int>& nums) {
int m = nums.size();
vector<int> dp(1 << m, 0);
vector<vector<int>> gcd_tmp(m, vector<int>(m, 0));
for (int i = 0; i < m; ++i) {
for (int j = i + 1; j < m; ++j) {
gcd_tmp[i][j] = gcd(nums[i], nums[j]);
}
}
int all = 1 << m;
for (int s = 1; s < all; ++s) {
int t = __builtin_popcount(s);
if (t & 1) {
continue;
}
for (int i = 0; i < m; ++i) {
if ((s >> i) & 1) {
for (int j = i + 1; j < m; ++j) {
if ((s >> j) & 1) {
dp[s] = max(dp[s], dp[s ^ (1 << i) ^ (1 << j)] + t / 2 * gcd_tmp[i][j]);
}
}
}
}
}
return dp[all - 1];
}
};
执行用时:52 ms, 在所有 C++ 提交中击败了94.23%的用户
内存消耗:9 MB, 在所有 C++ 提交中击败了27.89%的用户
复杂度分析
时间复杂度: O(2m × m2 + logC × m2),其中 m 为数组 nums 的长度,C = max(nums)。主要为「动态规划」的求解以及预处理每一对数字最大公约数的时间复杂度。
空间复杂度:O(2m × m2),其中 m 为数组 nums 的长度,主要为「动态规划」存储每一个状态和预处理中存储原数组中每一对元素最大公约数的空间开销。
author:LeetCode-Solution