数学建模——确定性时间序列分析方法

介绍

将预测对象按照时间顺序排成一组序列，称为时间序列。从时间序列过去的变化规律，推断今后变化的可能性及变化趋势、变化规律，这就是时间序列预测法。

时间序列模型，其实也是一种回归模型。其基本原理是，一方面承认事物发展的延续性，运用过去时间序列进行统计分析就能推断事物发展趋势；另一方面又充分考虑到偶然因素影响产生的随机性，为了消除随机波动的影响，利用历史数据，进行统计分析，并对数据做适当的处理，进行趋势预测。

优点：简单易行，便于掌握，能重复利用时间序列各项数据，计算速度快，对模型参数动有态确定能力，精度较好。
缺点：不能反映事物内在联系，不能分析两个因素的相关关系，只适合作短期预测。

确定性时间序列分析方法

1、时间序列的常见趋势

（1）长期趋势

时间序列朝着一定的方向持续上升或下降或留在某个水平的倾向。它反映了客观事物主要变化趋势，记为Tt；

（2）季节变动

序列按时间呈现短周期变化的规律，记为St；

（3）循环变动

通常是周期为一年以上的，由非季节因素一起的起伏波相似的波动，记为Ct；

（4）不规则变动

通常分为突然变动和随机扰动（变动），记为Rt。

常见的时间序列模型有以下几类

加法模型 yt=Tt+St+Ct+Rt；（常用）
乘法模型 yt=Tt×St×Ct×Rt；
混合模型 yt=Tt×St+Rt；yt=St+Tt×Ct×Rt；

其中，yt为观测值，随机变动Rt满足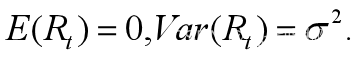

如果在预测时间范围内，无突然变动或者随机波动的方差σ2较小，并且有理由认为现在的演变趋势将持续发展到未来，可用一些经验方法进行预测。

2、时间序列预测的具体方法

2.1 移动平均法

设观测时间序列为y1,y2,…,yT。

一次移动平均值计算公式：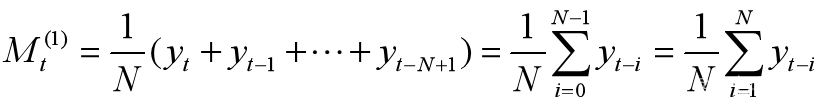

二次移动平均值计算公式：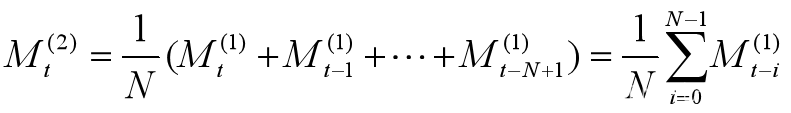

这里N<T,一般5≤N≤200.

（1）当预测目标的基本趋势在某一水平上下波动时，采用一次移动平均方法计算预测，即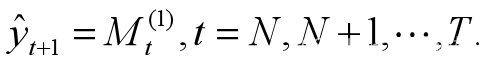

（2）当预测目标的基本趋势与某一直线相吻合时，采用二次移动平均法.

以上预测标准误差为

一般来说，N取多少为好，S越小越好。如果数据自带周期，N最好取周期值。

案例1

某企业1-11月的销售收入时间序列如表1所列，试用一次移动平均法预测12月的销售收入。

表1 1-11月销售收入记录

月份t	1	2	3	4	5	6
销售收入yt	533.8	574.6	606.9	649.8	705.1	772.0
月份t	7	8	9	10	11
销售收入yt	816.4	892.7	963.9	1015.1	1102.7

【符号说明】

t 时间变量t=1,2,…,11
yt 销售量记录值
n 移动平均项数
Mt 一次移动平均值,t=n,n+1,…,11
y(1) 预测值，t=5,6,…,12

【预测模型】

一次移动平均预测模型为：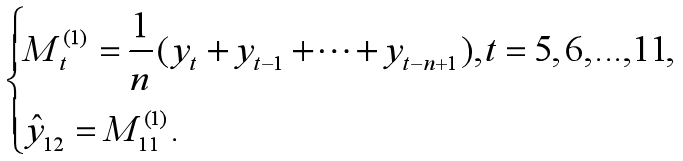

针对n=3，4，5，都做一次移动平均预测，将计算结果和误差都反映在表2.

先编写一个时间序列为yt,移动平均项n的预测与误差的程序yd1.m，再调用此函数计算不同n值的预测与误差，存放在表2进行对比

表2 n分别取3,4,5的预测对比

t	5	6	7	8	9	10	11	标准误差
yt	705.10	772.00	816.40	892.70	963.90	1015.10	1102.70	0.00
n=3	653.93	708.97	764.50	827.03	891.00	957.23	1027.23	60.73
n=4	634.10	683.45	735.83	796.55	861.25	922.03	993.60	92.37
n=5	614.04	661.68	710.04	767.20	830.02	892.02	958.16	124.63

function [M1,s]=yd1(yt,n)
t=length(yt);
yt1=[];
for k=n:t
    yr=yt(k-n+1:k);
    yr1=mean(yr);
    yt1=[yt1,yr1];
end
M1=[zeros(1,n-1),yt1];
yt21=yt(n+1:t);
yt22=M1(n+1:t);
yts=yt22-yt21;
s=(sum(yts.^2)/(t-n))^0.5;

yt=[533.8 574.6 606.9 649.8 705.1 772 816.4 892.7 963.9 1015.1 1102.7];
n=5;
[m1,s1]=yd1(yt,3);
[m2,s2]=yd1(yt,4);
[m3,s3]=yd1(yt,5);
S=[0,s1,s2,s3];
Y=[yt;m1;m2;m3];
B=[Y,S'];
xlswrite('d:\yidong1.xlsx',B);

由表2可见，n=3比n=4预测效果好，n=4比n=5预测效果好。用n=3的计算作预测，12月份销售量为1027.23.

2.2 一次指数平滑预测法

（1）预测模型

设时间序列为y1,y2,…,yt,…，α为加权系数，0<α<1，一次指数平滑公式为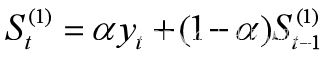

预测模型为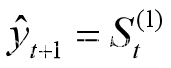

（2）加权系数的选择

（1）如果时间序列波动不大，比较平稳，则α取小一点，0.1-0.5，减小修正幅度，使预测模型包含较长的序列信息；

（2）如果序列具有迅速增加的变动趋势，α取大一点，0.6-0.8，使得预测模型灵敏度高一些，以便迅速跟上数据的变化。

（3）初始值的确定

一般选取最初几期实际值的平均值作为初始值。

案例2

就案例1中问题，用指数平滑预测法预测12月销售量。

就α=0.2,0.5,0.8分别作一次指数平滑预测，初始值为

即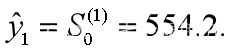

按照预测模型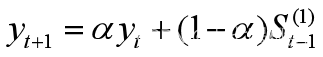计算不同α预测结果与误差，计入表3，进行对比做出决策。

function [s1,s]=expph1(yt,a)
n=length(yt);
s1(1)=mean(yt(1:2));
for k=2:n
    s1(k)=a*yt(k)+(1-a)*s1(k-1);
end
y11=s1-yt;
s=std(y11);

yt=[533.8 574.6 606.9 649.8 705.1 772 816.4 892.7 963.9 1015.1 1102.7];
[m1,s1]=expph1(yt,0.2);
[m2,s2]=expph1(yt,0.5);
[m3,s3]=expph1(yt,0.8);
s=[0,s1,s2,s3];
m=[yt;m1;m2;m3];
B=[m,s'];
xlswrite('d:\yd1.xlsx',B);

表3 不同权系数的指数平滑预测及其标准误差

月份	1	2	3	4	5	6
yt	533.80	574.60	606.90	649.80	705.10	772.00
a=0.2	554.20	558.28	568.00	584.36	608.51	641.21
a=0.5	554.20	564.40	585.65	617.73	661.41	716.71
a=0.8	554.20	570.52	599.62	639.76	692.03	756.01
月份	7	8	9	10	11	误差
yt	816.40	892.70	963.90	1015.10	1102.70	0.00
a=0.2	676.25	719.54	768.41	817.75	874.74	81.82
a=0.5	766.55	829.63	896.76	955.93	1029.32	28.33
a=0.8	804.32	875.02	946.12	1001.30	1082.42	11.20

由表3可以看出，α=0.8误差最小，选择系数α=0.8进行预测，12月份的销售量为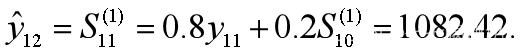

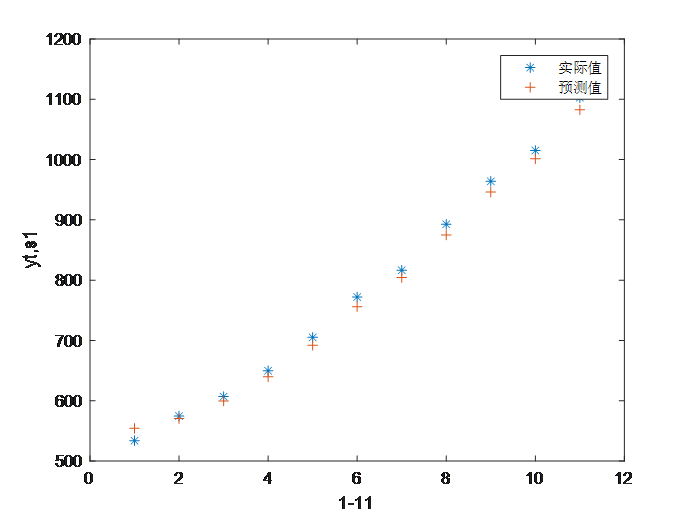
图2 预测值与实际值对比

从表2、表3和图2可以看出，预测值总是滞后于实际值。原因就是数据不满足模型要求（平稳型）。

3、差分指数平滑法

差分是改变数据趋势的根本方法（就像导数改变幂函数阶数一样）。如果数据呈现直线吻合型，差分后就呈现平稳性。

一阶差分指数平滑预测模型公式如下

【1】

公式【1】的第三个表示是就相当于：预测值=原值+差分(微分)的预测值.

案例3

对案例1问题用差分指数平滑法预测第12月的销售量。（取α=0.5）.

（1）先计算原始数据xt的差分，得到yt；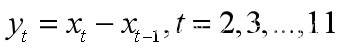

（2）对数据yt，取α=0.5做一次指数平滑预测，得到St；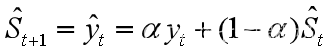

（3）作预测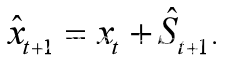

先编制一个给定时间序列和α的计算差分指数平滑预测的m函数，再调用m这个函数将计算结果汇总到表4.将预测结果与实测值对比如图3.差分指数平滑预测当α=0.5时，误差较小。

function [yc,err]=diffexpph(yt,a)
y=diff(yt);
[ym,s]=expph1(y,a);
y=[0,y];
ym=[0,ym];
n=length(y);
r=a*y(n)+(1-a)*ym(n);
ym=[ym,r];
for k=1:n
    yc(k+1)=ym(k+1)+yt(k);
end
xy=yc(2:end-1)-yt(2:end);
err=(sum(xy.^2)/10)^0.5;

yt=[533.8 574.6 606.9 649.8 705.1 772 816.4 892.7 963.9 1015.1 1102.7]; a=0.5;
[yc,err]=diffexpph(yt,a);
 plot(2:11,yt(2:end),'*',2:11,yc(2:end-1),'+'),
legend('实测值','预测值')
>> A1=[yt,0];
>> A=[A1;yc];
>> xlswrite('d:\diffexpph.xlsx',A)

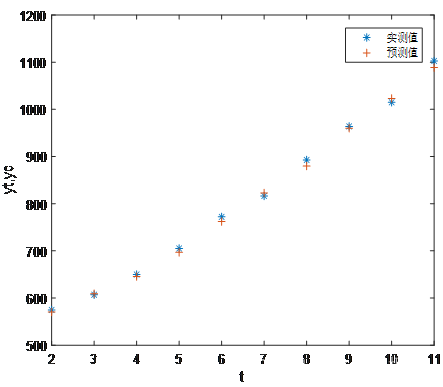
图3 差分指数平滑预测于实测对比

月份	1	2	3	4	5	6
实测yt	533.8	574.6	606.9	649.8	705.1	772
预测yc		570.35	609.025	645.5625	696.7813	762.0406
月份	7	8	9	10	11	12
实测yt	816.4	892.7	963.9	1015.1	1102.7
预测yc	822.6703	879.8852	960.0426	1023.171	1088.536	1183.218

表4 案例3差分指数平滑预测有关数据

由表4可以得到预测值，第12月销售量为1183.218.将不同α取值(0.1,0.3,0.6,0.9)计算结果汇总到表5，对比显示，差分指数平滑对线性吻合型数据，α取值越大，预测越准确。

yt=[533.8 574.6 606.9 649.8 705.1 772 816.4 892.7 963.9 1015.1 1102.7];
[yc1,s1]=diffexpph(yt,0.1);
[yc2,s2]=diffexpph(yt,0.3);
[yc3,s3]=diffexpph(yt,0.6);
[yc4,s4]=diffexpph(yt,0.9);
A1=[0,yt(2:end),0];
A2=[0,s1,s2,s3,s4];
A=[A1;yc1;yc2;yc3;yc4]';
B=[A;A2];
xlswrite('d:\diffexpph1.xlsx',B)

月份\α		0.1	0.3	0.6	0.9
1	0	0	0	0	0
2	574.6	570.35	570.35	570.35	570.35
3	606.9	610.725	609.875	608.6	607.325
4	649.8	643.7025	644.4625	646.24	648.7825
5	705.1	688.4523	692.6838	698.716	703.7583
6	772	746.577	755.1886	764.8064	770.7058
7	816.4	813.7693	820.382	822.5226	818.5206
8	892.7	861.6224	873.1574	882.389	889.7221
9	963.9	940.5202	953.7902	961.8156	964.1122
10	1015.1	1012.058	1022.023	1022.266	1017.121
11	1102.7	1067.202	1082.066	1091.006	1099.262
12	0	1158.352	1175.856	1185.623	1189.956
误差	0	19.44747	12.10722	6.799773	2.281841

表5 指数平滑不同α预测对比

4、具有季节性特点的时间序列的预测

具有季节特性的时间序列预测方法很多，这里介绍季节系数法，步骤如下：

（1）收集m年的每年各个季度或者各个月份（n个季度）的时间序列aij,i表示年份,i=1,2,…,m;j表示季度,j=1,2,…,n；

（2）计算所有数据的平均值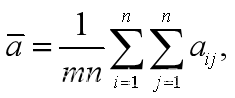

（3）计算同季度的算数平均数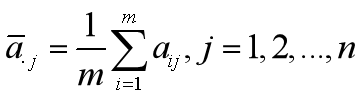

（4）计算季度系数

（5）预测计算

当时间序列是按季度给出，先求初预测年份（下一年）的年加权平均

再计算预测年份季度平均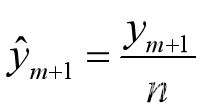

最后预测当年第j季度的预测值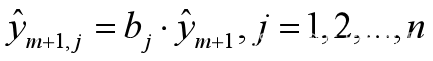

案例4

某商店某类商品1999-2000年各季度销售额如表6所示，预测2004年各季度销售额。

表6 1999-2003各季度销售额（单位：元）

年份\季度	1	2	3	4
1999	137920	186742	274561	175422
2000	142814	198423	265419	183512
2001	131002	193987	247556	169847
2002	157436	200144	283002	194319
2003	149827	214301	276333	185204
2004	145573	201170	272696	183901

模型求解：按照上面的规范步骤，2004年个季度销售额预测填入表6最后一行

B=xlsread('d:\jidu.xlsx');
A=B(:,2:end);
[m,n]=size(A);
a=sum(sum(A))/m/n;
aj=mean(A);
bj=aj/a;
yi=sum(A');
w=1:m;
yc=sum(yi.*w)/sum(w)/n;
ycj=yc*bj