1、晨星

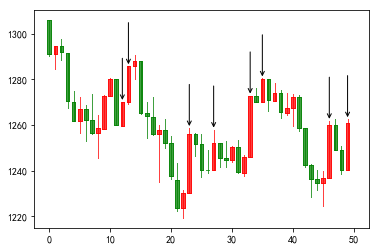
晨星也称作早晨之星，它是一种三日形态的K线组合，第一日是阴线，第二日价格振幅较小，第三日出现阳线，它的一般形态如下图所示。晨星的K线组合形态一般出现在下跌的趋势之后，预示着价格的上升回调。其在作为交易信号使用时，通常会结合交易量的指标。

import mpl_finance as mpf
import matplotlib.pyplot as plt
import talib
import pandas as pd
​
# 读取文件
df = pd.read_csv(r'xx')
df=df[0:40]
# 识别晨星的K线组合
nums = talib.CDLMORNINGSTAR(df['open'], df['high'], df['low'], df['close'])
# 可视化
fig = plt.figure()
ax = fig.add_subplot(111)
# 绘制K线图
mpf.candlestick2_ohlc(ax, df['open'], df['high'], df['low'], df['close'], width=0.6, colorup='red', colordown='green')
# 标注识别K线组合的位置
index = nums[nums==100].index.values
for i in index:
   ax.annotate(s='', xy=(i, df['high'][i]), xytext=(i, df['high'][i]+20), arrowprops= {'arrowstyle':'->','facecolor':'black'})
plt.show()
​

​

2、昏星

昏星（Evening Star），也称作黄昏之星。它与晨星类似，也是一种三日的K线组合形态，第一日为阳线，第二日价格振幅较小，第三日阴线，其常见形态如下图所示。但是它的作用于晨星反向，它通常出现在一段上升趋势中，预示着顶部的价格反转。

import numpy as np
import mpl_finance as mpf
import matplotlib.pyplot as plt
import talib
import pandas as pd
​
# 读取文件
df = pd.read_csv(r'xxx')
df=df[0:1000]
# 识别昏星的K线组合
nums = talib.CDLEVENINGSTAR(df['open'], df['high'], df['low'], df['close'])
# 可视化
fig = plt.figure()
ax = fig.add_subplot(111)
# 绘制K线图
mpf.candlestick2_ohlc(ax, df['open'], df['high'], df['low'], df['close'], width=0.6, colorup='red', colordown='green')
# 标注识别K线组合的位置
index = nums[nums==-100].index.values
print(index)
for i in index:
   ax.annotate(s='', xy=(i, df['high'][i]), xytext=(i, df['high'][i]+200), arrowprops= {'arrowstyle':'->'})
plt.show()
​

​

3、锤子线

锤子线（Hammer）是一种单日的K线形态，因其形态类似一把锤子，所以被命名为锤子线。它通常出现于一段下跌趋势之后，通常预示着价格见底。其形态通常表现在实体较短，下影线很长，没有上影线，如下图所示。另外，当锤子线的实体颜色是红色，而且下影线越长时，更具有参考意义。

import numpy as np
import mpl_finance as mpf
import matplotlib.pyplot as plt
import pandas as pd
import talib
​
# 读取文件
df = pd.read_csv(r'xxx')
df=df[0:80]
# 识别锤子线的K线模型
nums = talib.CDLHAMMER(df['open'], df['high'], df['low'], df['close'])
# 可视化
fig = plt.figure()
ax = fig.add_subplot(111)
# 绘制K线图
mpf.candlestick2_ohlc(ax, df['open'], df['high'], df['low'], df['close'], width=0.6, colorup='red', colordown='green')
# 标注识别K线组合的位置
index = nums[nums==100].index.values
for i in index:
    ax.annotate(s='', xy=(i, df['high'][i]), xytext=(i, df['high'][i] + 50), arrowprops={'arrowstyle': '->'})
plt.show()
​

4、上吊线

上吊线（Hanging Man），也称作倒锤子线，同锤子线一样，也是一种单日的K线形态，但意义和锤子线相反。其常出现于一段上升的价格走势之后，预示着价格反转。上吊线通常为较小的实体，伴随着较长的下影线，如下图所示。实体颜色为绿色且具有越长的下影线的上吊线形态的参考意义越强。另外需要注意的是，锤子线和上吊线在使用时，不仅仅需要判断其形态的出现，还需要结合其出现在价格区间的顶端还是底端，通常锤子线出现在价格区间底端，上吊线出现在价格区间顶端。

import numpy as np
import mpl_finance as mpf
import matplotlib.pyplot as plt
import pandas as pd
import talib
​
# 读取文件
df = pd.read_csv(r'xxx')
df=df[0:150]
# 识别上吊线的K线模型
nums = talib.CDLHANGINGMAN(df['open'], df['high'], df['low'], df['close'])
# 可视化
fig = plt.figure()
ax = fig.add_subplot(111)
# 绘制K线图
mpf.candlestick2_ohlc(ax, df['open'], df['high'], df['low'], df['close'], width=0.6, colorup='red', colordown='green')
# 标注识别K线组合的位置
index = nums[nums==-100].index.values
for i in index:
    ax.annotate(s='', xy=(i, df['high'][i]), xytext=(i, df['high'][i] +40), arrowprops={'arrowstyle': '->'})
plt.show()
​

5、捉腰带线

import numpy as np
import mpl_finance as mpf
import matplotlib.pyplot as plt
import pandas as pd
import talib
​
# 读取文件
df = pd.read_csv(r'F:\BaiduNetdiskDownload\Python量化金融编程从入门到精通 赠送资源\数据\第5章\SP_Daily_2000_2017.csv')
df=df[0:50]
# 识别捉腰带线的K线模型
nums = talib.CDLBELTHOLD(df['open'], df['high'], df['low'], df['close'])
# 可视化
fig = plt.figure()
ax = fig.add_subplot(111)
# 绘制K线图
mpf.candlestick2_ohlc(ax, df['open'], df['high'], df['low'], df['close'], width=0.6, colorup='red', colordown='green')
# 标注识别K线组合的位置
index = nums[nums==100].index.values
for i in index:
    ax.annotate(s='', xy=(i, df['high'][i]), xytext=(i, df['high'][i] + 20), arrowprops={'arrowstyle': '->'})
plt.show()
​