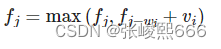这篇文章主要是对EMNLP2021上的论文Raise a Child in Large Language Model: Towards Effective and Generalizable Fine-tuning进行讲解。论文标题有些抽象，但是用作者的话来说，这篇论文的思想可以归结为两个词：Child Tuning

虽然这篇文章主要针对NLP任务以及NLP相关的模型，但实际上我看完之后觉得这是一个通用的方法，CV领域也可以使用。具体来说，目前预训练模型的参数非常大，在下游任务中，我们只能用有限的训练集对模型进行微调，有一种螳臂当车的感觉，因此作者提出了一种新的微调方法——Child Tuning。如果用一句话概述其思想那就是：在反向传播过程中，我们不用更新所有的参数，只更新某些参数即可，而这些被更新的参数所对应的网络结构，我们叫做Child Network（子网络）

如上图所示，上面一行是正常的反向传播过程，其中
$$\Delta w_0=-\eta \frac{\partial \mathcal{L}}{\partial {\mathbf{w}}_0}\text{\hspace{1em}(1)}$$
下标0不是指某一个参数，而是指第0个迭代过程，$\eta$是学习率。对于下面一行来说，$\Delta {\mathbf{w}}_0$有一部分被MASK掉了，导致这里面的梯度为0
$$\Delta w_0=-\eta \frac{\partial \mathcal{L}}{\partial {\mathbf{w}}_0}\odot M\text{\hspace{1em}(2)}$$
其中，$M$矩阵内的元素非0即1，$\odot$是矩阵内的元素做对应位置相乘。我们可以用两步来概括Child Tuning的过程：

1. 在预训练模型中发现并确认Child Network，并生成对应Weights的0-1 MASK
2. 反向传播计算完梯度后，仅对Child Network中的参数进行更新

所以现在的问题是如何确认Child Network？

How to find Child Network?

实际上我们并不需要真的找到Child Network，只要确定矩阵$M$即可。论文提供了两种算法用于生成矩阵$M$，分别是任务无关算法Child_Tuning_F (F for Task-Free)以及与具体任务相关的算法Child_Tuning_D (D for Task-Drivern)

Child_Tuning_F

任务无关算法的意思是与你具体所做的具体任务没有关系，都可以使用这个算法，是一种通用的方法。具体来说，此时**$M$是根据伯努利分布生成的**
$$\begin{array}{rl}{\mathbf{w}}_{t+1}& ={\mathbf{w}}_t-\eta \frac{\partial \mathcal{L}\left({\mathbf{w}}_t\right)}{\partial {\mathbf{w}}_t}\odot M_t\\ M_t& \sim \text{Bernoulli}(p_F)\end{array}\text{\hspace{1em}(3)}$$
其中$p_F\in [0,1]$是一个超参数，他控制着Child Network的大小，如果$p_F=1$，则Child Network就是原网络，此时Child Tuning就是Fine Tuning；如果$p_F=0$，则没有任何参数会被更新。下面是我写的一个简单模拟的代码帮助大家理解

import torch
from torch.distributions.bernoulli import Bernoulli

gradient = torch.randn((3, 4)) # 这里用一个随机生成的矩阵来代表梯度
p_F = 0.2
gradient_mask = Bernoulli(gradient.new_full(size=gradien.size(), fill_value=p_F))
gradient_mask = gradient_mask.sample() / p_F # 除以p_F是为了保证梯度的期望不变
print(gradient_mask)

gradient *= gradient_mask
print(gradient)

Bernoulli是一个类，生成的gradient_mask是一个对象，我们需要调用这个对象的sample()方法才能得到一个矩阵。其中比较重要的一点是虽然我们得到了0-1 MASK，但我们需要将这个MASK内所有的1扩大$1/p_F$倍以维持梯度的期望值

别的梯度都不在了，活着的梯度要带着其他人的意志坚强的反向传播下去啊！

Child_Tuning_D

考虑到存在不同的下游任务，作者提出一种与具体任务相关的算法Child_Tuning_D，它可以检测出对目标任务最重要的子网络（或者参数）。具体来说，作者采用Fisher信息估计法来寻找与特定下游任务高度相关的参数。形式上，模型参数$\mathbf{w}$的Fisher Information Matrix(FIM)定义如下：
$$\mathbf{F}(\mathbf{w})=\mathbb{E}\left[\left(\frac{\partial \log p(y\mid \mathbf{x};\mathbf{w})}{\partial \mathbf{w}}\right){\left(\frac{\partial \log p(y\mid \mathbf{x};\mathbf{w})}{\partial \mathbf{w}}\right)}^{\top }\right]\text{\hspace{1em}(4)}$$
其中，$x,y$分别是输入和输出，由此我们可以推出第$i$个参数的Fisher信息如下：
$${\mathbf{F}}^{(i)}(\mathbf{w})=\frac{1}{|D|}\sum _{j=1}^{|D|}{\left(\frac{\partial \log p\left(y_j\mid {\mathbf{x}}_j;\mathbf{w}\right)}{\partial {\mathbf{w}}^{(i)}}\right)}^2\text{\hspace{1em}(5)}$$
其中，$|D|$是所有样本的数量。作者认为，参数对目标任务越重要，其Fisher信息越大，因此Child Tuning是由Fisher信息最高的那些参数组成，此时Child Network的比例为
$$p_D=\frac{\mid \mathcal{C}\mid }{\mid \mathcal{C}\mid +\mid \bar{\mathcal{C}}\mid }\in (0,1]\text{\hspace{1em}(6)}$$
其中$| \bar{\mathcal{C}}| $表示非子网络，当$p_D=1$时，Child Tuning就退化为了Fine Tuning。实际上Fisher信息的计算是相当耗时的，如果我们每次反向传播后都去计算一次所有参数的Fisher信息，然后找出最大的前几个是很麻烦的，因此作者提出在真正开始训练之前，我们先对所有样本进行一次完整（一个Epoch）的前向传播和反向传播，此时计算出Fisher信息最高的那些参数，以及此时确定的Child Network以后就不再变化了，就以这一次所选定的为准

下面给出计算Fisher信息的代码

def calculate_fisher():
    gradient_mask, p_F = {}, 0.2
    train_loader = torch.utils.data.DataLoader(train_dataset, batch_size, shuffle=True)
    N = len(train_dataloader) # N = |D|
    for name, params in model.named_parameters():
        if 'layer' in name:
            gradient_mask[params] = params.new_zeros(params.size())
    for batch in train_loader:
        outpus = model(**batch)
        loss = outpus['loss'] if isinstance(outpus, dict) else outputs[0]
        loss.backward()

        for name, params in model.named_parameters():
            if 'layer' in name:
                torch.nn.utils.clip_grad_norm(params, 1)
                gradient_mask[params] += (params.grad ** 2) / N
        model.zero_grad()
    
    r = None
    for k, v in gradient_mask.items():
        v = v.view(-1).cpu().numpy() # flatten
        if r is None:
            r = v
        else:
            r = np.append(r, v)
    
    # polar = np.percentile(a, q) # a中有q%的元素小于polar
    polar = np.percentile(r, (1-p_F)*100)
    for k in gradient_mask:
        gradient_mask[k] = gradient_mask[k] >= polar
    print('Polar => {}'.format(polar))

    return gradient_mask

Proof

如果这篇论文就讲了这些东西，很大概率是中不了EMNLP的，之所以被录用了，我个人觉得和这篇论文里大量的证明有关，作者证明了使用Child Tuning可以帮助模型逃离局部极小值点，接下来我尝试着把论文中的证明部分说清楚

首先我们假设${\mathbf{g}}^{(i)}$是给定样本${\mathbf{x}}^{(i)}$时参数$\mathbf{w}$的梯度，并且它服从正态分布${\mathbf{g}}^{(i)}\sim N(\frac{\partial \mathcal{L}}{\partial \mathbf{w}},{\sigma }_{\mathbf{g}}^2{\mathbf{I}}_k)$，定义$\mathbf{g}=\sum _{i=1}^{|\mathcal{B}|}\frac{{\mathbf{g}}^{(i)}}{|\mathcal{B}|}$，则有
$$\Delta \mathbf{w}=-\eta \sum _{i=1}^{|\mathcal{B}|}\frac{{\mathbf{g}}^{(i)}}{|\mathcal{B}|}\odot M=-\eta \mathbf{g}\odot M\text{\hspace{1em}(7)}$$
对于$\mathbf{g}$，我们有
$$\mathbb{E}[\mathbf{g}]=\frac{\partial \mathcal{L}}{\partial \mathbf{w}},\Sigma [\mathbf{g}]=\frac{{\sigma }_{\mathbf{g}}^2{\mathbf{I}}_k}{|\mathcal{B}|}\text{\hspace{1em}(8)}$$
设$\hat{\mathbf{g}}=\frac{\mathbf{g}}{p}\odot M$，其中$p$是$p_D$或$p_F$（看你用的哪种算法），则
$$\begin{array}{rl}\mathbb{E}[\hat{\mathbf{g}}]& =\mathbb{E}[\frac{1}{p}\mathbf{g}\odot M]\\ & =\frac{1}{p}\mathbb{E}[\mathbf{g}\odot M]\\ & =\frac{p}{p}\mathbb{E}[\mathbf{g}]\\ & =\frac{\partial \mathcal{L}}{\partial \mathbf{w}}\end{array}\text{\hspace{1em}(9)}$$
上面的公式推导其实并不严格，例如分子的$p$是从哪来的就没法解释，分子的$p$只有可能是$\mathbb{E}[M]$的结果，可是$M$是个矩阵，矩阵的期望怎么就变成一个数了呢？但要强行解释也可以，因为将$M$中所有的1加起来除以$M$内的所有元素似乎也是等于$p$的

设$\widehat{g_i},g_i$分别是$\hat{\mathbf{g}},\mathbf{g}$第$i$维度上的值，那么有$\widehat{g_i}=\frac{g_i}{p}\odot M_i$
$$\begin{array}{rl}\mathbf{D}[\widehat{g_i}]& =\mathbb{E}[{\widehat{g_i}}^2]-(\mathbb{E}[\widehat{g_i}]{)}^2\\ & =p\mathbb{E}[(\frac{g_i}{p}{)}^2]-(\mathbb{E}[\widehat{g_i}]{)}^2\\ & =\frac{\mathbb{E}[g_i^2]}{p}-(\mathbb{E}[\widehat{g_i}]{)}^2\\ & =\frac{(\mathbb{E}[g_i]{)}^2+\mathbf{D}[g_i]}{p}-(\mathbb{E}[\widehat{g_i}]{)}^2\\ & =\frac{(\mathbb{E}[g_i]{)}^2+\mathbf{D}[g_i]}{p}-(\mathbb{E}[\frac{g_i}{p}\odot M_i]{)}^2\\ & =\frac{(\mathbb{E}[g_i]{)}^2+\mathbf{D}[g_i]}{p}-(\mathbb{E}[g_i]{)}^2\\ & =\frac{\mathbf{D}[g_i]}{p}+\frac{(1-p)(\mathbb{E}[\widehat{g_i}]{)}^2}{p}\end{array}\text{\hspace{1em}(10)}$$
因此
Σ [ g ^ ] = Σ [ g ] p + ( 1 − p ) diag { E [ g ] } 2 p = σ g 2 I k p ∣ B ∣ + ( 1 − p ) diag { E [ g ] } 2 p (11) \begin{aligned} \Sigma[\hat{\mathbf{g}}] &= \frac{\Sigma[\mathbf{g}]}{p} + \frac{(1-p)\text{diag}\{\mathbb{E}[\mathbf{g}]\}^2}{p}\\ &=\frac{\sigma^2_{\mathbf{g}}\mathbf{I}_k}{p|\mathcal{B}|} + \frac{(1-p)\text{diag}\{\mathbb{E}[\mathbf{g}]\}^2}{p} \end{aligned}\tag{11} Σ[g^​]​=pΣ[g]​+p(1−p)diag{E[g]}2​=p∣B∣σg2​Ik​​+p(1−p)diag{E[g]}2​​(11)
最终我们就得到
$$\begin{array}{rl}\mathbb{E}[\mathbf{\Delta }\mathbf{w}]& =-\eta \frac{\partial \mathcal{L}}{\partial \mathbf{w}}\\ \Sigma [\mathbf{\Delta }\mathbf{w}]& =\frac{{\eta }^2{\sigma }_{\mathbf{g}}^2{\mathbf{I}}_k}{p|\mathcal{B}|}+\frac{(1-p){\eta }^2\mathrm{diag}{\left\{\frac{\partial \mathcal{L}}{\partial \mathbf{w}}\right\}}^2}{p}\end{array}\text{\hspace{1em}(12)}$$
特别地，当参数$\mathbf{w}$训练到局部极小值点时，$\frac{\partial \mathcal{L}}{\partial \mathbf{w}}=0$，此时$\mathbb{E}[\Delta \mathbf{w}]=0,\Sigma [\Delta \mathbf{w}]=\frac{{\eta }^2{\sigma }_{\mathbf{g}}^2{\mathbf{I}}_k}{p|\mathcal{B}|}$，我们注意到$\Sigma [\Delta \mathbf{w}]$是关于$p$的一个递减函数，$p$越大，$\Sigma [\Delta \mathbf{w}]$越小，极端情况是$p=1$，此时Child Tuning退化为Fine Tuning，并且$\Sigma [\Delta \mathbf{w}]$最小，相当于它的变化量每次都不大，因此就很难跳出局部极小值点；$p$越小，$\Sigma [\Delta \mathbf{w}]$越大，相当于它的变化量每次都很大，因此比较容易跳出局部极小值点

个人总结

这篇论文刚读的时候觉得很厉害，但了解之后就觉得这其实就是一个反向传播版的Dropout，实际的创新并没有特别大，包括其中提到的Fisher信息也并不是这篇论文提出来的。再就是论文中的实验确实很多，实验结果表明，相比于Fine Tuning大约可以提升1.5～8.6个点不等。最后要说一下这篇论文的公式证明部分，我个人觉得这篇论文的证明其实没有很严谨，例如为什么一个矩阵的期望就变成一个数了。总的来说这个方法可以作为打比赛时候的一个Trick来使用