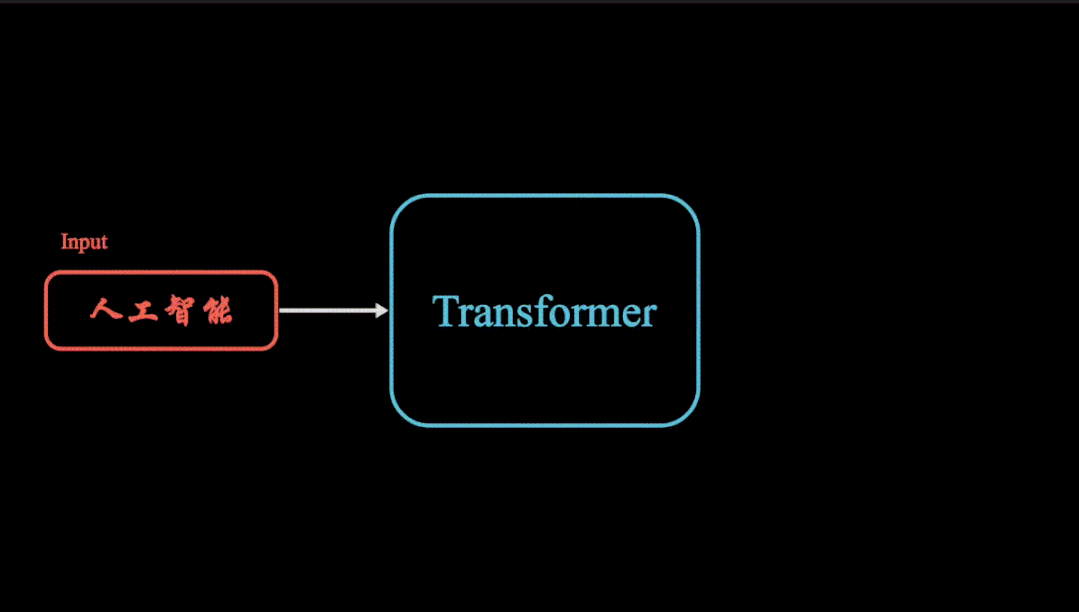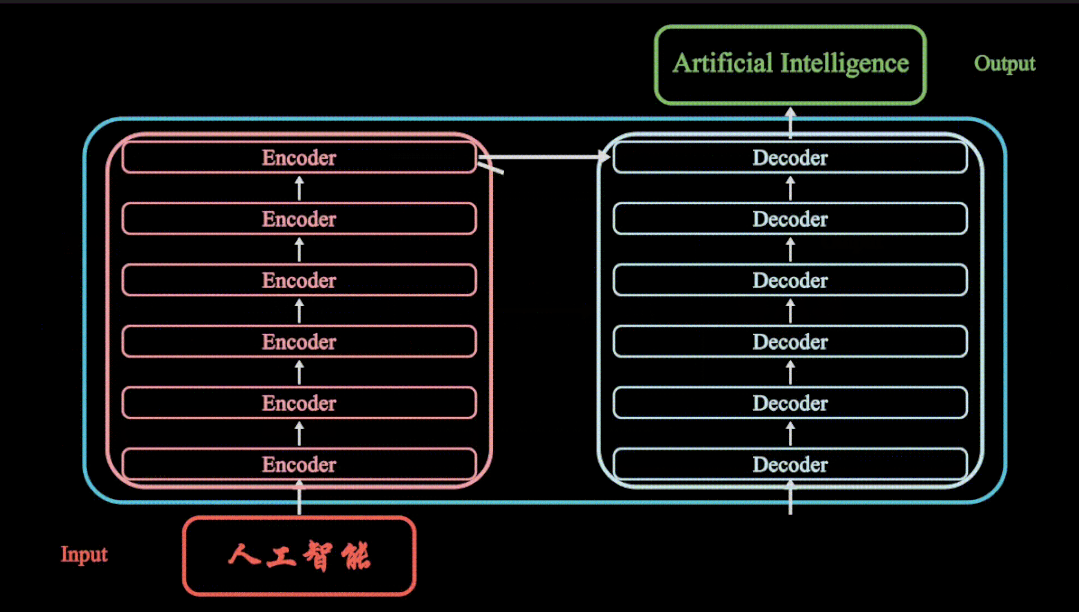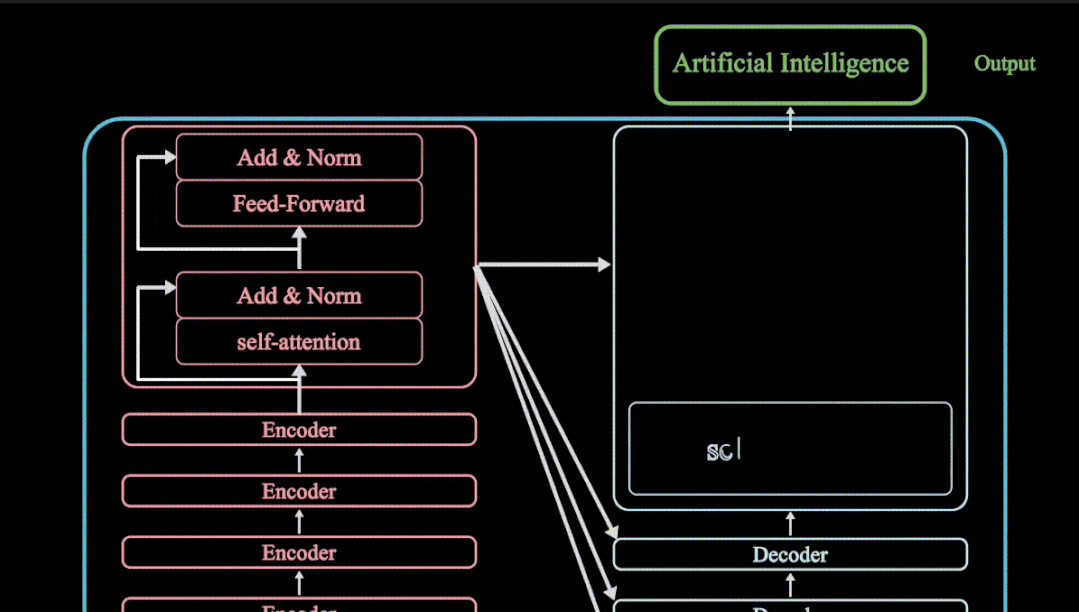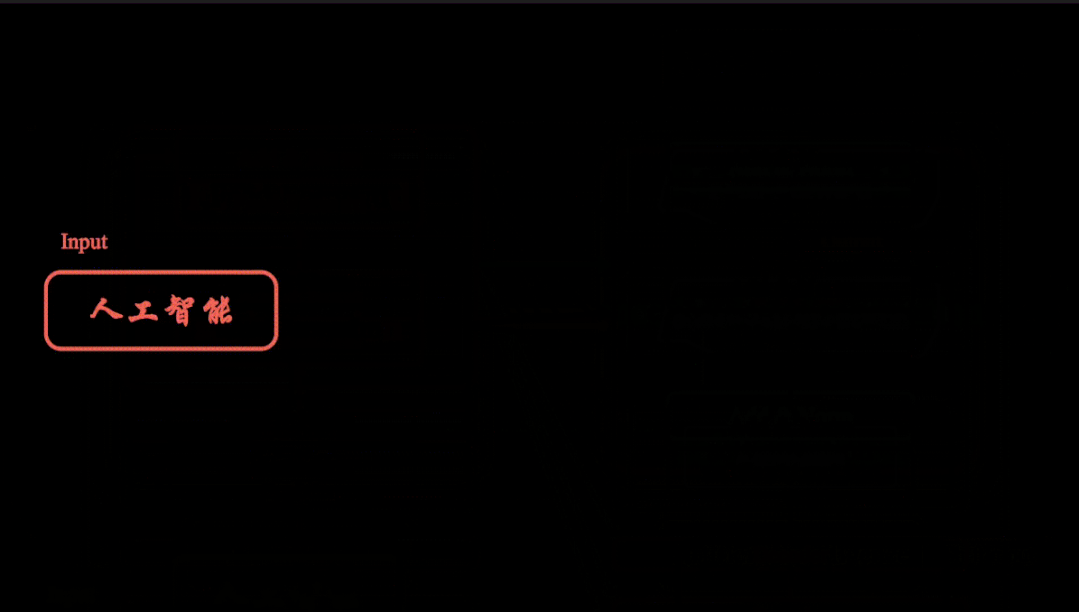
Web 应用防火墙 (WAF) 是保护 Web 应用的必要措施。如今,WAF 需要在部署环境不断扩展但人员技能有限的情况下,保护数量日益增长的应用。那么防火墙是什么?作为一家提供多云应用安全和应用交付的公司,F5为保护Web应用又打造出哪些产品?一起来看看。
如今,多云环境、API 安全功能扩展、合作伙伴集成即时可用、可用性和可视化增强以及提高自动化程度已经成为基本要求。谈论防火墙是什么,就不会忽视F5的Web应用产品。早期,F5的Web应用防火墙产品ASM主要针对传统OWASP TOP 10进行防范。F5 ASM为每个Web APP提供了一个安全策略,与该Web APP相关的所有功能配置都绑定到该安全策略上,不同的安全策略之间的配置相互独立。
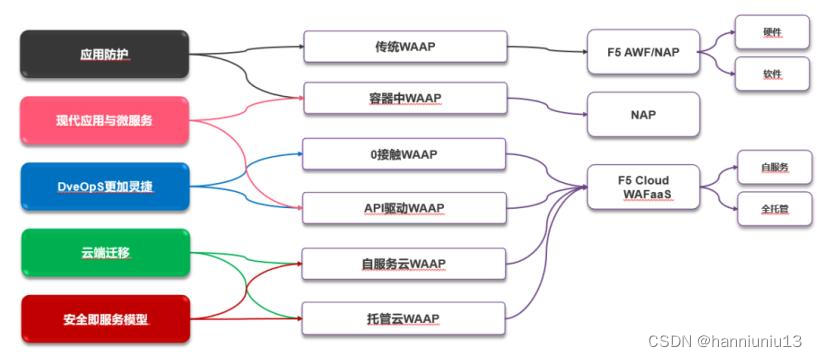
随着企业应用架构的迁移,在用户端,防护不能仅仅针对Web应用,还需要增加针对API、机器人的防护,这就需要更新型的工具。为此,F5推出了Advanced WAF(API 安全— 新一代WAF ),即高级Web应用防火墙(Advanced Web Application Firewall),旨在通过领先的应用安全实力, 针对日趋复杂的应用威胁,为用户打造一体化的解决方案。
为了帮助企业应对多云以及边缘端的挑战,F5将Advanced WAF(API 安全— 新一代WAF )产品的能力,包括安全引擎、安全处理能力,迁移到了NGINX容器和公有云SaaS服务,以及边缘的Web应用中。F5将这种可以帮助客户在不同应用架构、不同应用部署环境中提供一致性的高级安全防护效果,安全能力伴随用户的应用变迁而变化的解决方案称之为F5应用安全防护方案。
F5的WAF的优势性是行业内有目共睹的。在2022年第3季度The Forrester Wave?:Web应用防火墙报告中,Forrester Research选出了12家最出色的Web应用防火墙 (WAF) 提供商,然后对它们进行研究、分析和评分,以评比它们相较于彼此的表现水平,其中F5的WAF被赞誉表现强劲。
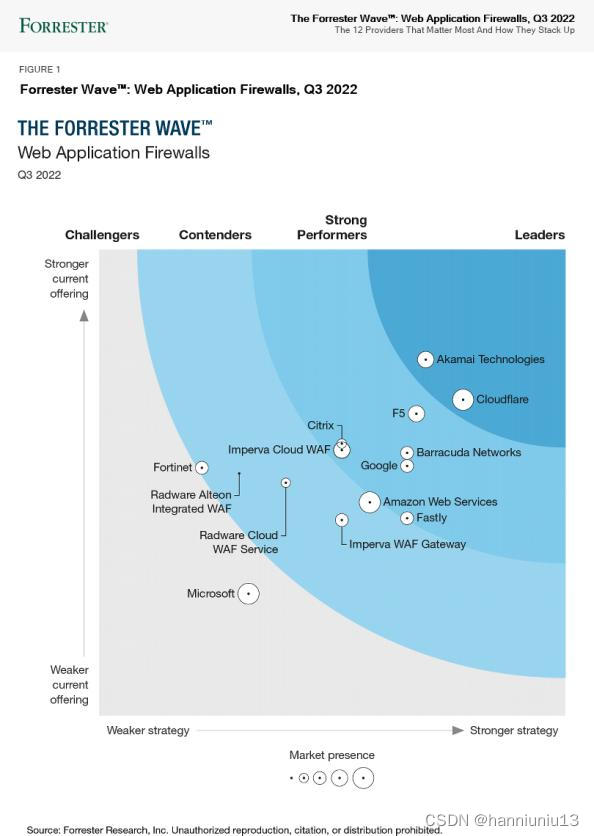
回到防火墙是什么?有哪些优秀的解决方案?这一问题,通过上述的分析,相信已经了解到,F5及其WAF解决方案能够满足企业在选择和运营WAF方面提出的必备条件。不可否认的是,F5能为企业带来了全数据通路的安全防护能力,为企业加速数字化转型保驾护航。