数字化信道

数字化信道主要包括多相滤波和DFT两个模块。

多相滤波

多相滤波，就是将滤波器系数按照相数进行重排。
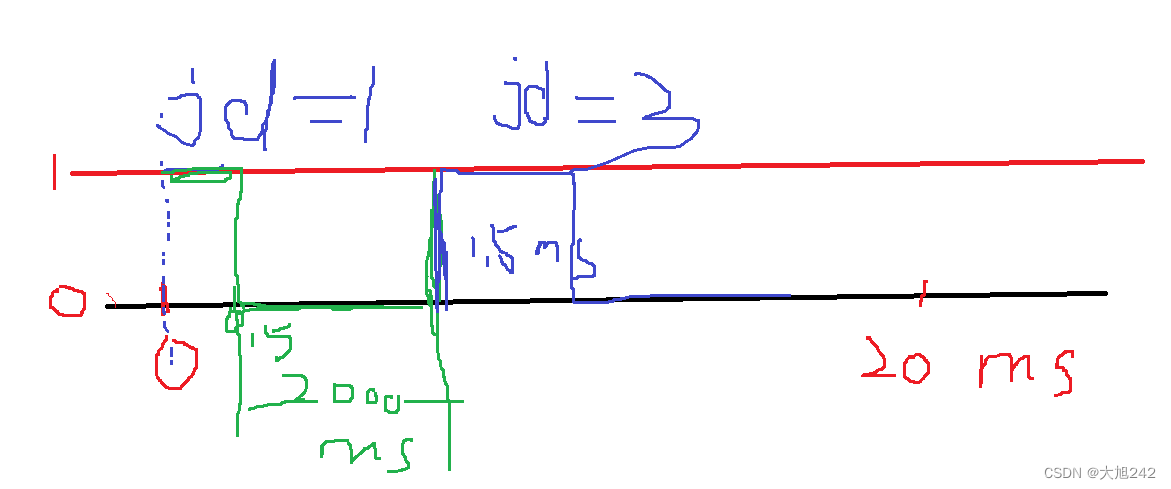
在D倍抽取后，整个频带的频谱将混叠在0频附近 $[-\frac{F_s}{2D} ,\frac{F_s}{2D})$ 。因此，多相滤波器的每一个分支都包含原始信号的所有频谱。
抽取后的信号经过每个分支的滤波器进行滤波。
通过数学方法，还原出原始的每个频带的频谱，DFT其实现方案之一。
抽取滤波，将各个分支数据进行相加即可得到。

DFT

DFT和IDFT的实现仅旋转因子不同，因此，可以相互实现。
DFT实现IDFT的步骤
- 将输入取共轭
- 进行DFT运算
- 将输出取共轭
- 幅度*1/N即可
  $x(n)=IDFT(X(k))=\frac{1}{N}\{DFT(X^*(k))\}^*$

数字化信道代码

目标：采样率16M，将信号拆分成4x4M。

% 设计滤波器
h=fir1(255,1/4);
% 测试信号
N=1e3; % 测试点数
D=4; % 相数
fs=16e6; % 16MHz
t=(0:N-1)/fs;
f0=0.1e6;
f1=4.2e6;
f2=8.3e6;
f3=11.6e6;
s=0.9*exp(1i*2*pi*f0*t)+0.8*exp(1i*2*pi*f1*t)+0.7*exp(1i*2*pi*f2*t)+0.6*exp(1i*2*pi*f3*t);
% 绘制信号幅度谱
figure(1);
f=0:fs/length(s):fs-fs/length(s);
plot(f,fftshift(10*log10(abs(fft(s))))); 
xlabel('frequency(Hz)');
ylabel('amp(dB)');

% 多相化
hn=reshape(h,D,[]);
sn=reshape(s,D,[]);lter_out=zeros(size(sn));
chn_out=zeros(size(sn));
for i=1:D
	filter_out(i,:)=conv(sn(D-i+1,:),hn(i,:),'same'); % 滤波，原理同filter一样，时域卷积
end

for i=1:size(sn,2)
	chn_out(:,i)=D*ifft(filter_out(:,i)); % 因为IFFT计算过程缩小了D倍
end

figure(2);
for i=1:D
	subplot(4,1,i);
	plot(real(chn_out(i,:)));
	xlabel(['channel ',sprintf('%d',i-1)]);
end

在这里插入图片描述
信道化输出时域